Тепловые явления при поверхностном пластическом деформировании

пренебречь. Действительно, в квазистационар-ной стадии процесса при установившемся тепловом режиме можно считать, что околоконтакт-ные участки инструмента, непрерывно подвергающиеся тепловому воздействию, практически оказываются прогретыми до максимальной температуры. Относительно же детали контактная область непрерывно перемещается, встречаясь все время с ненагретыми точками. Вследствие этого температурные градиенты в детали значительно превосходят величину градиента в направлении деформирующего инструмента. Таким образом, теплоотводом в инструмент в ква-зистационарном режиме без существенного ущерба для точности можно пренебречь.

В соответствии со сказанным можем записать для ультразвукового упрочнения и обработки Q д ≈ Q дет . Для алмазного выглаживания следует учитывать и теплоту, выделяющуюся от работы сил трения. Следовательно Q д + Q т = Q дет . При рассматриваемых методах ППД источники теплоты локальные, образующиеся в результате пластической деформации.

При ультразвуковом упрочнении на постоянное статическое усилие, передающееся со стороны деформирующего инструмента (индентора), накладывается переменное периодическое усилие с частотой ультразвуковых колебаний. В связи с этим тепловую мощность следует считать переменной величиной, зависящей от времени. Поскольку общая работа состоит из работы, производимой постоянной силой Р ст и периодической, то в соответствии с принципом суперпозиции может рассматривать два независимых источника теплоты. Мощность первого определяется следующим образом:

P_r„A'y lOOO кал q = —ст------- ---

1 М 60 сек где К – коэффициент трения, υ – скорость, М – механический эквивалент теплоты.

Мощность источника при обработке и выглаживании определяется подобным же образом. Работа пластического внедрения индентора, производимая переменным периодическим усилием, совершаемая с частотой ξ циклов в минуту. В этом случае средняя мощность источника

_ Аю кал q0(t) М , сек где А – работа пластического внедрения.

В действительности усилие внедрения в течение каждого цикла меняется. Следовательно, изменяется и мощность источника. Очевидно, что для вычисления максимальных температур надо знать наибольшую (амплитудную) мощность источника q 0 (мощность в конечный момент внедрения). Можно принять, что усилие, а, следовательно, и мощность изменяются по косинусоидальному закону. В этом случае запишем f(t)=q 0 cosωt .

При исследовании температурных полей, образующихся в процессе ППД температуру в зоне деформации можно рассматривать как результат наложения локального температурного поля, возникающего в момент деформации данного участка изделия и общего температурного поля, вызываемого притоком тепла от ранее деформированных участков. На общее температурное поле влияют форма и размеры обрабатываемой детали, время предшествующей обработки, характер теплообмена с окружающей средой и общая тепловая мощность источников. В то же время для оценки величины общего поля практически безразличен характер распределения источников в детали. Вследствие сказанного для определения общего нагрева в каждом конкретном случае можно воспользоваться какой-либо из известных зависимостей схематизируя форму источника и вид движения по возможности наиболее простым способом. Например, локальное температурное поле в основном зависит от формы источников и закона распределения мощности их тепловыделения и практически не зависит от остальных перечисленных выше факторов.

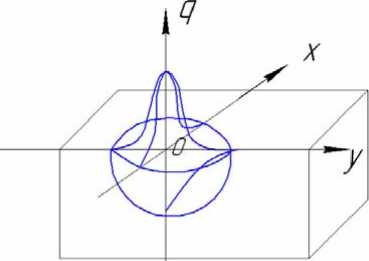
Основываясь на кривых микротвердости в очаге деформации, характеризующих степень деформации, принимаем сферический источник теплоты с распределением его интенсивности по трем пространственным координатам по нормальному закону (рис. 1). В этом случае можно записать

F (x, y, z, t) = — exp(-kR2), cY где qm – максимальная интенсивность тепловыделения, с – теплоемкость, γ – удельный вес, к – коэффициент сосредоточенности тепловой мощности, характеризующий форму кривой нормального распределения.

Z

Рис. 1. Схема нормально-сферического источника теплоты

Для ультразвукового упрочнения рекомендуется радиус отпечатка принять равным условному пятну нагрева r н , где интенсивность тепловыделения q i составляет 0,05 от наибольшей интенсивности в центре отпечатка. В этом случае К =30/ r н ². Так как локальное температурное поле практически не зависит от формы изделия, то поверхность обрабатываемой детали можно считать плоской, представляя само изделие полупространством -∞V в направлении оси ОХ, то в подвижной системе координат, движущейся вместе с источником, поставленная задача запишется в виде:

dT         dT

= a A T + V    + Q ( x , y , z , t )

dt             dt

(-∞<х, у<∞; 0≤z, t<∞)

Нами получено общее решение задачи (для произвольного распределения источников и произвольной зависимости их интенсивности от времени) в форме четырехкратного интеграла. Для его приведения к виду, пригодному для расчетов, требуется задать контактный вид закона распределения q=q(x,y,z,t). Если в процессе накатывания шариком интенсивность источников можно считать постоянной во времени, то при ультразвуковом упрочнении интенсивность меняется по периодическому закону. При любых методах упрочняющей обработки нас интересует максимальная температура квазистационарной стадии процесса, так как время переходного режима обычно мало по сравнению с общей длительностью процесса. Однако получение асимптотических решений при t→∞ классическими методами затруднительно, поскольку приходится иметь дело с трудоемкими предельными переходами в несобственных интегралах. Еще более сложную задачу представляет выделение периодической составляющей решения для случая движущихся источников с периодически меняющейся интенсивностью.

Для определения локальной температуры квазистционарного состояния при действии источника с периодически меняющейся интенсивности целесообразно перейти в плоскость изображений по Лапласу, т.к. операционные методы позволяет срезу выделить периодическую составляющую решения, избегая трудоемких предельных переходов в несобственных интегралах. После преобразования Лапласа найдем температуру

T ( x ,, z , p ) = 1 ds   F ( ξ , η , s , p )exp[ ^υ ( x - ξ )] x

.4 π Q _{0    -∞}               .2 Q

x [ ¹ exp( - R ₁ 'V p + α ) + 1 exp( - R ₂ " V p + α )] d ξ d η

R1      a          R2       a где T и Q – изображения температуры и интенсивности источников; α=σ2/4Q, р – параметр преобразования Лапласа

При определении локальной составляющей температурного поля наибольший интерес представляет максимальная температура очага деформации. Будем считать, что максимальная контактная температура близка к температуре точки 0 (0, 0, 0), в которой интенсивность источников тепла наибольшая. В этом случае можно ограничиться определением температуры Т(0,0,0,t)=Т(t) в начале отсчета подвижной системы координат. Следует отметить, что при больших скоростях движения источника максимум температуры может быть несколько смещен от центральной точки (0, 0, 0) в сторону отставания по оси ОХ. Полагая в равенстве (1) Х=У=Z=0 и замеча я, что при этом R ₁ = R ₂ = R = ξ ² + η ² + s ² найдем изображение максимальной температуры контакта при произвольном распределении источников

T ( p ) = T (0,0,0, p ) = ¹ x 2 πα

∞d ∞F(ξ    ) 1   (-υξ)   (-R Vp x ds F(ξ,η, s, p) exp(-  )exp(-       )dξdη

0    -∞          R     2 a          α

Пpи ультразвуковом упрочнении действуют два независимых источника теплоты. В соответствии с этим на температуру Т1 , возникающую от действия источника постоянной мощности q1 , накладываются температурные колебания Т(t) возникающие вследствие дополнительного воздействия переменного источника q0 (t). Последний зависит от времени и изменяется по синусоидальному или косинусоидальнону законам. Схематически изменение контактной тем- пературы во времени показано на рис. 2. Считая интенсивность переменного теплового источника q0(t) изменяющейся во времени с частотой ω по косинусоидальной зависимости, для общей тепловой мощности имеем:

q0 ( t )= q1+ q0 cosωt где q0 – амплитудное значение переменной составляющей тепловой мощности.

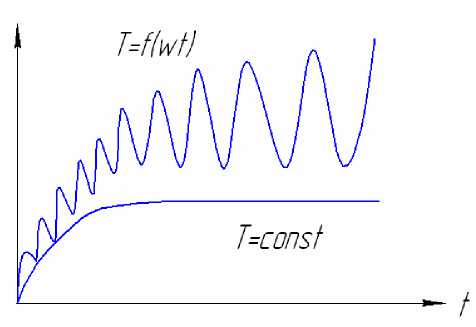
Рис. 2. Изменение контактной температуры во времени

В силу линейности уравнения теплопроводности результирующую температуру Т(t) можно представить в квазистционарной стадии состоящей из постоянной составляющей температуры порождаемой постоянным источником q 1 , и переменной составляющей Т(t), возникающей от действия источника q 0 (t)= q 1 + q 0 cos ωt

Т(t)= Т 1 + Т 0 (t)

При этом каждую из составляющих контактной температуры можно искать отдельно сводя решение к двум самостоятельным задачам. Для определения переменной составляющей установившейся температуры Т0(t) воспользуемся (с некоторыми модификациями) методом, предложенным Г. Деч [2]. Зависимость осциллирующей мощности источника от времени удобней представить в комплексной форме, полагая q0 (t)= q0 exp(iωt)

Для вычисления максимальной температуры контактной области Т(t) при ультразвуковом упрочнении следует сложить амплитудное значение переменной составляющей контактной температуры. К найденной таким образом локальной температуре следует затем прибавить температуру общего поля, определяемую каждый раз для заданных условий обработки, и формы обрабатываемой детали.

Рассмотрим наиболее часто встречающийся случай, когда обрабатываемая поверхность является цилиндрической, а отношение скорости вращения детали к подаче достаточно велико.

При определении температуры общего ущерба для точности можно довольствоваться грубой схематизацией формы и распределения тепловых источников. В рассматриваемом случае можно представить источник распределенным по всей контактной поверхности, описываемой за один оборот изделия. Этот кольцевой источник, поступательно движущийся в направлении оси цилиндра, в свою очередь можно представить как узкую полосу, перемещающуюся по поверхности полупространства. Тогда среднюю поверхностную температуру поля в установившимся режиме можно найти по формуле [3]:

т = ^qcpl- [ ch &) Ko( Щ) + sh (Щ) K 1( Щ)] nA 2 Q 2 Q 2 Q 2 Q где l – половина ширины полосы контакта (радиус отпечатка); qср – усредненный тепловой поток, равный тепловой мощности отнесенной к середине поверхности пояса; К0(х) и К1(х) – функции акдональда нулевого и первого порядков соответственно, υs – скорость движения источника.

При экспериментальном исследовании температуры изменялась величина статического (нормального) усилия и скорость, т.е. основные параметры процесса ультразвукового упрочнения и обкатки. Сопоставление теоретических и экспериментальных данных показало хорошую сходимость результатов. Из графиков, представленных на рис. 3 видно, что максимальная температура в контакте существенно зависит от усилия и скорости обработки, т.е. от параметров, определяющих количество теплоты, образующейся при деформации.

При накатывании шариком с усилием 1500 Н и скоростью 30 м/мин максимальная температура не превышает 100-1300С. С ростом усилия до 3400 Н и скорости до 150 м/мин температура повышается до 240-2500С. При ультразвуковом упрочнении наблюдается аналогичная зависимость. Анализ теоретических и экспериментальных данных позволил установить, что максимальное расхождение между ними, как правило, не превышает 12-16%.

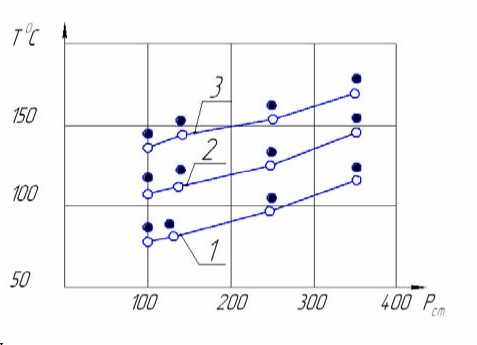
Рис. 3. Результаты определения температуры в контакте при ультразвуковом упрочнении:

1) υ=30 м/мин; 2) υ=8 м/мин; 3) υ=150 м/мин; о- экспериментально; • - теоретически

Использование аналогичного метода расчета температуры на поверхности контакта позволяет производить проверку выбранных режимов по допустимой температуре нагрева. Последнее особенно необходимо при применении интенсивных режимов упрочнения.