Термоанемометрический преобразователь массовой скорости воздушного потока

Исследование аэродинамики летательных аппаратов и определение условий работы оборудования в их отсеках требует результатов измерения вектора массовой скорости воздушного потока. Этот параметр изменяется в широких пределах, а процесс его изменения является нестационарным.

По совокупности предъявляемых требований к преобразователям вектора массовой скорости наиболее целесообразно использовать термоанемометрический метод постоянного тока. При использовании этого метода необходимо решить проблемы измерения нестационарных значений вектора массовой скорости при значительном изменении температуры, а также турбулентности воздушного потока.

Известно, что интенсивность теплообмена тела, омываемого воздушным потоком, неравномерна по поверхности из-за различной толщины и характера движения воздуха в пограничном слое.

Для того чтобы использовать это свойство тела при измерении вектора массовой скорости воздушного потока, необходимо найти оптимальную форму и размеры первичного преобразователя.

Оптимальной формой первичного преобразователя вектора скорости является центрально-симметричная выпуклая фигура, идеал которой – сфера. К центрально-симметричным выпуклым фигурам относятся следующие: тетраэдр, куб, додекаэдр и т. д. Вид фигуры рационально выбирать из условия оптимизации разрешающей способности и трудоемкости измерительного комплекса, т. е. первичного и вторичного преобразователей, регистрирующего устройства и пр. Если первичный преобразователь будет иметь малое количество граней, то трудоемкость изготовления первичного преобразователя будет низкой, однако алгоритм определения направления перемещения воздуха будет сложен, и, наоборот, если первичный преобразователь будет иметь большое количество граней, то трудоемкость изготовления заметно возрастает, а алгоритм упрощается. Поэтому был выбран додекаэдр (рис. 1), фигура с 12 гранями.

У поверхности летательных аппаратов и в их отсеках может быть турбулентный характер перетекания воздуха. Отсюда грань первичного преобразователя должна воспринимать среднюю массовую скорость воздуха, а не ее флуктуации. Для получения среднеинтегральной интенсивности теплообмена, характеризующейся определенным вектором массовой скорости воздушного потока, размеры чувствительных элементов, нанесенных на грани первичного преобразователя, должны быть больше микромасштаба турбулентности. С другой стороны, первичный преобразователь, введенный в воздушный поток, должен быть настолько мал, чтобы вызываемое им возмущение картины течения было минимально.

Руководствуясь перечисленными требованиями, были выбраны размеры чувствительного элемента (4 × 5 мм) и первичного преобразователя (диаметр описанной сферы додекаэдра 15 мм).

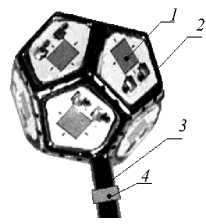
Рис. 1. Преобразователь вектора массовой скорости воздушного потока ДВС:

1 – чувствительные элементы термоанемометра; 2 – корпус;

3 – трубка для крепления преобразователя в заданной точке отсека; 4 – термометр на трубке

Первичный преобразователь вектора модуля массовой скорости воздушного потока (рис. 1) состоит из корпуса 1 , чувствительных элементов термоанемометра 2 , закрепленных на корпусе преобразователя, трубки 3 , служащей для крепления преобразователя в заданной точке отсека, и термометра 4 , закрепленного на трубке.

Измерение температуры воздушного потока необходимо для введения поправок на показания термоанемометрических чувствительных элементов при определении модуля массовой скорости.

Вторичный преобразователь вектора массовой скорости представляет собой источник постоянного тока и усилитель выходного сигнала первичного преобразователя.

Алгоритм определения вектора модуля массовой скорости следующий:

• 1.    Получают градуировочную характеристику, т. е. зависимость выходного сигнала с чувствительных элементов термоанемометра в вольтах от температуры воздушной среды T_air и модуля массовой скорости J_air

• 2.    Измеряют температуру воздушной среды.

• 3.    Определяют модуль массовой скорости по зависимости приведенного к количеству чувствительных элементов интегрального выходного сигнала со всех чувствительных элементов термоанемометра от модуля массовой скорости для измеренной температуры.

• 4.    Измеряют давление воздушной среды P_air .

• 5.    Рассчитывают плотность воздушной среды по формуле

  P ar = 3,4852 - 10 - 3 P air I T ar ,           (1)

• 6.    Если необходимо, то определяют модуль скорости воздушной среды по формуле

(произведения скорости W_air и плотности воздушной среды ρ _air ) в виде таблиц (например, табл. 1).

где давление – в паскалях, а температура – в кельвинах.

W ar = J ar I P air ,                 (2)

где массовая скорость – в кг/(м2·c), а плотность – в кг/м3.

Направление воздушной среды определяется двумя углами α и β в соответствии с номером (рис. 2) или совокупности номеров чувствительных элементов (граней) с минимальными значениями выходного сигнала (табл. 2).

Угол α отсчитывается от оси Х в плоскости XOY против часовой стрелки, угол β – от оси Х в плоскости XOZ также против часовой стрелки.

Погрешность определения направления в диапазоне от 0 до 6,28 ср. определяли на основе результатов лабораторных исследований на стенде для моделирования воздушного потока переменной температуры и плотности. Погрешность в зависимости от величины модуля массовой скорости в диапазоне 0,2-50 кг/(м² - с) составляет 0,3–0,6 ср.

Оценивание динамических и статических погрешностей измерения модуля проводилось на основе построения математических моделей нестационарного конвективно-лучистого теплообмена преобразователя в отсеке летательного аппарата.

Таблица 1

Выходной сигнал с чувствительных элементов преобразователя в зависимости от угла α обтекания его воздушным потоком J _air = 2,46 кг/(м²·c) при T _air = 283 К

Угол α, рад	Грань
	1	2	3	4	5	6	7	8	9	10	11	12
0	3,18	3,19	3,25	3,46	3,03	3,31	3,05	3,31	3,00	2,52	2,55	2,50
0,52	3,25	3,29	3,13	3,57	3,03	3,08	2,68	3,33	3,60	2,61	2,46	2,52
1,04	3,05	3,07	2,94	3,62	2,93	2,47	2,42	3,25	3,59	2,70	2,30	2,49
1,57	2,64	2,14	2,57	3,23	3,15	2,23	2,18	2,41	3,36	3,22	2,38	2,75
2,09	2,54	2,04	2,63	3,22	3,06	2,25	2,23	2,31	3,19	2,96	2,92	3,02
2,61	2,10	2,06	2,09	3,38	3,05	2,29	2,50	2,80	3,41	3,05	2,95	3,07
3,14	2,28	2,15	2,19	2,97	3,30	2,61	3,11	2,76	3,49	3,34	3,06	3,23
3,66	2,23	2,36	2,10	2,67	3,23	3,21	3,38	3,00	3,09	3,25	3,16	3,29
5,23	2,91	2,86	2,82	2,64	2,53	3,15	3,20	3,13	2,77	2,39	2,61	2,81
5,76	3,05	2,95	2,95	2,72	3,09	3,26	3,21	3,11	2,63	2,39	2,66	2,43

Таблица 2

Углы а и в направления воздушного потока при номерах чувствительных элементов (граней) с минимальными значениями выходного сигнала

Грани 3, 1, 2 1, 2, 6 2, 6, 7 6, 7, 11 7, 11, 12 11, 12, 10 12, 10, 9 10, 9, 4 Угол α , рад 3,14 2,51 1,88 1,25 0,63 0 5,64 5,01 Угол β , рад 3,14 0 0 0 0,52 0 0,52 0 Номер грани 9, 4, 3 4, 3, 1 3, 2, 8 2, 7, 8 7, 12, 8 12, 9, 8 9, 3, 8 4, 1, 5 Угол α , рад 4,38 3,76 3,14 1,88 0,63 5,64 4,38 2,51 Угол β , рад 2,61 3,65 2,40 1,98 1,18 1,18 1,98 4,32 Номер грани 1, 6, 5 6, 11, 5 11, 10, 5 10, 4, 5 1 2 3 4 Угол α , рад 1,25 0 5,01 3,76 3,14 2,51 3,76 4,38 Угол β , рад 4,32 5,22 5,56 5,22 3,76 0,70 0,70 3,76 Номер грани 5 6 7 8 9 10 11 12 Угол α , рад 0 1,88 1,25 0 5,01 5,64 0,63 0 Угол β , рад 4,70 3,76 0,70 1,57 0,70 3,76 3,76 0,70 a (AF \T ,-T A^c.£ }F,x sen sen an ,cl      air 0cl cl

Математическое моделирование позволяет найти изменение температуры термоанемометра от неста-ционарности конвективно-лучистого теплообмена, а также от количественных различий интенсивности теплообмена в реальных условиях и при тарировке термоанемометра. По найденным изменениям температуры определяют названные погрешности.

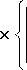
T , an , cl

^^^^^^»

T

Tcl

+ I' n R an

= 0,

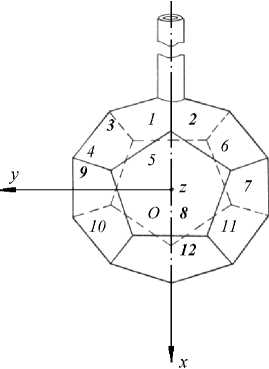
Рис. 2. Схема размещения чувствительных элементов на преобразователе вектора массовой скорости ДВС: 2 , 3 , 7 , 8 , 9 , 12 - видимые грани; 1, 4, 5, 6, 10, 11 - невидимые грани

Математические модели термоанемометров, соответственно, для реальных условий и тарировки имеют следующий вид [1]:

' sen^Tt, sen ^{+ a} sen ⁽ t ) ^Fsen ^{[ T}an

— T air ( t )] +

0 sen , in , cv   sen , in , cv

T an

T in , c v ( t )

) +

+ C„F. F

0 sen , eq   sen , eq

Г T an ( t ) I⁴

-

T eq ( t )

I' n R an ( t ) = 0;

где C_sen – теплоемкость преобразователя; α _sen – коэффициент теплоотдачи преобразователя при конвективном теплообмене; F_sen – площадь теплоотдающей поверхности преобразователя при конвективном теплообмене; T_an – температура термоанемометров; c ₀ – постоянная Стефана–Больцмана; ε _{sen , in , cv} – приведенная степень черноты излучения преобразователя и внутренней поверхности обшивки; F_{sen , in , cv} – площадь взаимной поверхности излучения преобразователя и внутренней поверхности обшивки; T_{in , cv} – температура внутренней поверхности обшивки; s sen _eq - приведенная степень черноты излучения преобразователя и окружающего преобразователь оборудования; F_{sen , eq} – площадь взаимной поверхности излучения преобразователя и окружающего преобразователь оборудования; T_eq – температура поверхности окружающего преобразователь оборудования; I_an – электрический ток, протекающий по чувствительным элементам; R_an – сопротивление чувствительных элементов; t - время; s _cl - приведенная степень черного излучения преобразователя при тарировке; F_cl – взаимная поверхность излучения преобразователя и окружающих поверхностей при тарировке; T_{an , cl} – температура термоанемометров при тарировке; T_cl – температура окружающих термоанемометры поверхностей при тарировке.

Уравнения (3), (4) при определенных упрощениях с учетом критериальных соотношений для коэффициентов теплоотдачи преобразователя α _sen можно привести к следующему виду:

Г ’ t , sen

+ 9 1 J^( t )[ T_a n

- T ar ( t )] +

+ 9 з

an

T in , cv ( t ) 100

+

+ ^ 4

+ 9 5

T an

T eq

( t ) 1 4 '

+ ^an ( t ) = 0;

9 1 J9_r( t )[T _a„_d - T ar ] +

T , an , cl

T ( t )

+ ^an ( t ) = 0,

где 9 1 , 9 2 , к , 9 5 - параметры математической модели.

Или в общем виде уравнения (5), (6) можно записать следующим образом:

Y = F(Y , t , 0 );                  (7)

Y (0) = Yq, где 0 = [91,92, к, 95]T - вектор параметров модели.

Получение достоверных величин параметров модели расчетным путем не представляется возможным. Поэтому их оценивание проведем путем параметрической идентификации по данным летных экспериментов и тарировки.

Для численного решения системы (7) используется метод Розенброка второго порядка аппроксимации, согласно которому вычисление решения на одном шаге численного интегрирования происходит следующим образом:

Y,+1 = Y, + a k1 + (1 + a) k2;(8)

(I - ahFy (Yn, tn, 0))k1 = hF(Yn, tn + ah, 0);(9)

( I + a hF y ( Y n , t n , 0 )) k 2 = hF ( Y n +a k 1 , t n + 2 a h , 0 ); (10)

a = 1 -1/20,5,(11)

где h – шаг интегрирования; I – единичная матрица; F_y – матрица Якоби системы (7).

Решение задачи оценивания параметров осуществляется путем минимизации суммы квадратов невязок между измеренными в ходе испытаний значениями температур и соответствующими значениями температур, полученными в ходе расчета по уравнениям модели. При этом используется квазиньютоновский метод минимизации, согласно которому очередное направление поиска определяется из системы уравнений:

B^kS^k =- df ( 0 ^k ),               (12)

где B^k – оценка матрицы вторых производных в текущей точке 0 ^k ; df - градиент функции f .

Для вычисления градиента минимизируемой функции необходимо иметь производные от решения системы обыкновенных дифференциальных уравнений по параметрам, которые называются функциями чувствительности.

В программном обеспечении функции чувствительности вычисляются в результате одновременного решения системы (7) и системы обыкновенных дифференциальных уравнений, которая получается из нее в результате дифференцирования по параметрам и имеет вид

Y v (0) = F y Y v + F v ; (13)

Y v (0) = 0.

При этом используется экономичный алгоритм вычисления функции чувствительности, предложенный в работе [2].

Значения полученных параметров v приведены в табл. 3.

Динамическая и статическая погрешности определяются разностью значений температуры T_an термоанемометра в реальных условиях и при тарировке. Входящие в уравнения (3), (4) величины температур T_cv , T_air , T_eq и модуля массовой скорости J_air примем соответствующими результатам летного эксперимента самолета для режимов, пропорциональных режимам программ летных ресурсных испытаний. Доверительные интервалы рассматриваемых погрешностей массовой скорости в диапазоне 0,2–50 кг / (м²·с) равны 4·10^–2 кг / (м²·с) при доверительной вероятности 0,95.

Таким образом, разработан термоанемометрический преобразователь массовой скорости воздушного потока в форме додекаэдра. Предложен метод оценивания динамической погрешности измерения и исследованы методические погрешности измерения.