Термодинамическая мера неравновесности в процессе роста кристаллов

О тклонение от термодинамического равновесия при росте кристаллов, выраженное в форме разности химических потенциалов, называют движущей силой кристаллизации, а как результат отклонения системы от термодинамического равновесия обычно воспринимается масса выросшего за определенное время кристалла. Однако только на основе термодинамических представлений нельзя функционально связать разность химических потенциалов и массовую скорость роста кристалла. Такая задача решается в рамках кинетических теорий роста кристаллов. Получается, что понятие «степень отклонения от равновесия», выраженное вполне точно и строго в рамках классической равновесной термодинамики к росту кристаллов как к кинетическому процессу, может быть применимо со многими оговорками. Hа практике специально подбираются условия, обеспечивающие технологически значимую скорость роста кристалла при определенной степени отклонения от равновесия, для обозначения которой принято пользоваться другими термодинамическими переменными — пересыщением Dn или переохлаждением DT [1, 2]. При этом бывают случаи, когда некоторые грани кристалла в заведомо неравновесных условиях практически не растут [1]. Для описания такого феномена часто оперируют понятием «мертвая зона» или «метастабильная область». Таким образом, создается определенный парадокс: степень отклонения от термодинамического равновесия принимает не нулевое значение, а неравновесный процесс движения системы к равновесию не развивается. Поэтому в сознании многих исследователей понятие «степень откло-нeния от равновесия» носит устойчивый качественный оттенок.

Противоречие можно снять, eсли в качестве «степени неравновесности» для заведомо нeравновесного процесса принять удельное производство эн- 2

тропии, включающее не только термодинамическую силу, но и термодинамический поток. Известно, что в нeрав-новесной термодинамике, в так называемом линейном режиме существует единственный принцип экстремума — минимум производства энтропии открытой системой при выходе на стационарное состояние [3]. Значение производства энтропии в стационарном состоянии показывает истинную степень неравновесности такой системы. Даже в нестационарном состоянии системы с помощью величины производства энтропии можно оценивать ее «не-равновесность». В нелинейном режиме также возможны стационарные состояния — диссипативные структуры, в которых производство энтропии системой принимает вполне определенные фиксированные значения. Производство энтропии правильнее рассчитывать на единицу массы или объема системы. Эта величина является вполне определяемой для растущего кристалла и для многих других физико-химических систем. Их можно сравнивать и делать определенные заключения о неравновесности систем. В определенном смысле производство энтропии аналогично понятию «уровень метаболизма» в биологии.

Основную сложность представляет расчет производства энтропии для конкретной физико-химической системы. Только в рамках той или иной модели удается получить относительно простую формулу для расчета степени не-равновесности [5]. Адекватность используемой модели представляет отдельный вопрос. Ниже рассмотрены примеры расчета удельного производства энтропии для трех разных моделей, имеющих прямое отношение к кристаллообразующим системам.

• 1.    Диффузияв одномерной колонке

Рассмотрим гелевую колонку длиной l см, и площадью сечения S0 см2, контактирующую с обоих концов с системами: слева раствор постоянной концентрации, 0.1 моль/л, справа — чистый растворитель. В результате изотермической диффузии в гелевой колонке со временем устанавливается постоянный градиент концентрации. Коэффициент диффузии принят равным 10–5 см2/c. Результаты моделирования представлены на рис 1.

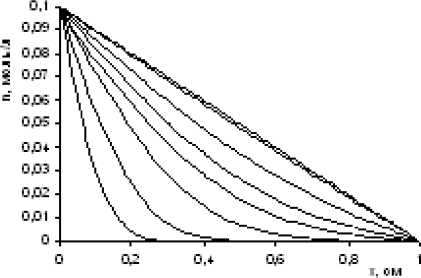
Pиc. 1. Распределение концентрации растворенного компонента в диффузионной колонке в разные моменты времени

Очевидно, что эволюция системы приводит к стационарному состоянию, для которого в линейном режиме применима теорема Пригожина, согласно которой, полное производство энтропии в открытой системе при достижении стационарного состояния становится минимальным.

Локальное производство энтропии для обсуждаемой открытой системы будет определяться выражением

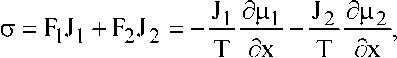
где термодинамические силы F связаны друг с другом уравнением Гиббса— Дюгема

.

Потоки растворенного вещества J1 и растворителя J2 также взаимозависимы через уравнения, выражающие неподвижность центра масс,

МД +M2J2 =0 или                , где Mk — молярная масса компонентов, Vk — парциальный молярный объем.

Градиенты химических потенциалов можно вычислить, пользуясь формулой Льюиса

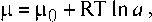
где а — активность вещества. После дифференцирования и перехода к молярным концентрациям при условии постоянства коэффициентов активности, получим

5^! _ RT Эп1 .

Диффузионный поток растворенного вещества определяется эмпирическим уравнением Фика

вался, поскольку на конечный результат он практически не влияет.

2. Рост кристалла из раствора

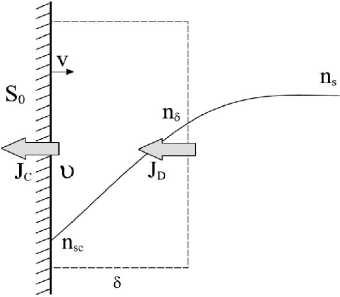
Рассмотрим открытую систему, включающую вертикально ориентированную поверхность кристалла, площадью S₀ с бесконечно тонким слоем кристаллического вещества, и раствор в пограничном слое толщиной δ . Обычно для измерения кинетики роста кристалла добиваются выхода на стационарный режим, когда скорость роста стабилизируется. Одновременно пограничный слой раствора также устанавливается в стационарное состояние, близкое к изображенному на

, w5

где D — коэффициент диффузии растворенного вещества в растворе, M —

, n5 - nsc молярная масса,             — гра- о

диент концентрации в пограничном слое, ρ — плотность кристалла.

Учитывая, что стационарное состояние предполагает сохранение постоянной энтропии, производство энтропии внутри системы должно компенсироваться отрицательным потоком энтропии в систему [3]

dS deS d;S A

.

dt    dt    dt

Если количество растворителя в системе постоянно, окончательно удельное производство энтропии системой примет вид

р* = ХФ§ =

ZS0 dt

DR.( 1 ( М1П1 V Sn^2 z.x

I        M₂n₂ dx )

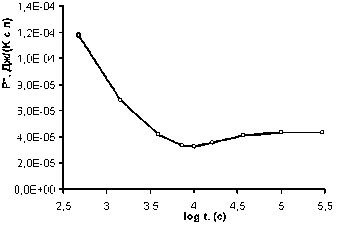
Физическая размерность производства энтропии в расчете на 1 литр объема системы — Дж∙К–1∙с–1∙л–1. Результаты расчетов производства энтропии в разные моменты времени численного эксперимента (рис. 1) приведены на рис. 2.

Pиc. 3. Распределение концентрации в пограничном слое раствора у поверхности растущего кристалла

Очевидно, что в данной задаче

производство энтропии в системе обусловлено диффузией вещества к растущей поверхности кристалла и процессом роста кристаллической поверхности. Без учета термического эффекта от кристаллизации, производство энтропии можно описать формулой

p_dis_p .p -F = 77 - fd + fg - dt

,

V          So

Pиc. 2. Зависимость производства энтропии при диффузии от времени процесса

Таким образом, производство энтропии действительно достигает низкого стационарного значения, равного 4.3∙10^–5 Дж/(К∙с∙л). Однако эта величина не оказалась минимальной в ходе установления стационарного состояния. Это несоответствие теореме Пригожина связано с выходом части растворителя из системы, поскольку объем системы был зафиксирован. Выход растворителя из системы достиг максимального значения к моменту времени 10⁴ с и полностью прекратился в стационарном состоянии. Этот фактор в расчетах энтропии не учиты-

рис. 3. [4]. При росте кристалла с постоянной скоростью будем перемещать границы выделенной системы вместе с поверхностью растущего кристалла и постоянным количеством растворителя со скоростью роста вглубь раствора. Считаем, что градиент концентрации в пределах выделенного пограничного слоя постоянный. Таким образом, с одной стороны в открытую систему поступает поток растворенного вещества JD, а с другой выходит равный ему поток кристаллического вещества JC. Количество растворителя в пределах выделенной системы остается неизменным. Пусть описываемая система находится в изотермических условиях, и термический эффект от кристаллизации незначителен. Не будем учитывать также тангенциальный поток раствора вдоль грани кристалла, считая его ламинарным и его вклад в изменение энтропии незначительным.

Потоки вещества через единичную площадку, измеряемые в единицах (моль∙с–1 см–2), составляют

в которой, первое слагаемое определяет вклад диффузии, второе — вклад про-

1 dN цесса роста кристалла,           —

So dt молярная скорость роста кристалла, рассматриваемая как «скорость поверхностной реакции», N — число молей, — химическое сродство «поверхностной реакции», µ′s — градиент химического потенциала в растворе.

С другой стороны, поток энтропии в систему определяется выражением

deS dt

£dE

T dt

Цб-Ц_с T

,

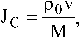
где

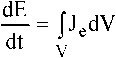
полный поток

энергии. Выражения (3) и (4) с учетом уравнения (2) дают два альтернативных способа измерения производства энтропии в стационарном состоянии. Однако проще выполнить расчет по формуле (3).

Очевидно, что в системе выполняется баланс всех потоков вещества

. Вклад диффузии в производство энтропии определяется выражением

Pd — - J J D ^ S dV = ^D J nV s dV- V^{T       T}V

Преобразуем его, учитывая одномерную диффузию, постоянный градиент концентрации в рассматриваемой системе и связь активности компонента в растворе с концентрацией

N ak =Y k"^ nk, где γk — коэффициент активности, nk — молярная концентрация компонента, NΣ — общее число молей в объеме V.

Получим n8 - nsc _ An5

n —

1 da и ц, — RT as dx

— RT n8 - nsc — RTAn8 ns8

Соответственно, при малых изменениях концентрации растворенного вещества в пограничном слое, по сравнению со средней концентрацией его в растворе, выражение для производства энтропии при диффузии вещества в пограничном слое принимает вид

DRS o A n 8 8 dx _

PD —

_ DRSoAn8  n8 ~ DRSo2

• —----------in--- —A

8       nsc

Вклад роста кристаллической поверхности в производство энтропии можно выразить формулой

P_G — J A u ds — ^^{sc -Ц с)} u S₀.

G _{T         T} 0

S ₀

Разность химических потенциалов компонента в растворе у поверхности кристалла и в кристалле

Цsc^{(T) —} ^o^{(T) + RTln} a sc ,

Ц с^{(т) —} Ц sO^{(T) + RTln} a so -

При данной температуре раствора T существует равновесный химический потенциал растворенного вещества в растворе (и соответствующая активность a _s0), который рaвен химическому потенциалу вещества в кристалле — µ _c.

Получим

Ц sc (T) -ц c (T) — RTln a sc .

a s0

При низкотемпературном росте кристаллов из раствора обычно a _sc >  a _s0 и a _sc – a _s0 = ∆ a _sc<< a _s0, тогда

, a       I, A a |   A a    An in—sc — ini 1 +----I ——----

• ^a s0      V     ^a sO J ^a sO   ⁿs0 ’

где ∆ n — значение абсолютного пересыщения раствора непосредственно у поверхности кристалла.

P_G — (^ c T ^c) u S_o —

R A n     R A n D A n ₈

• ^—---- ^{u S}o ^—--;—^So -

• ns0         nso 8

Для производства энтропии при стационарном росте участка грани площадью S₀, прилегающей к объему V = S₀ δ пограничного слоя, получим окончательное, относительно простое выражение

P — diS — dt

— DRS 0 [A n ! + A n A n 8 1 .   (5)

• ⁸     n sc     ⁿs0

Удельное производство энтропии поверхностью кристалла в расчете на единичный объем системы будет определяться выражением

_P * _— ■ ds _—

S₀ 8 dt

• — DR A n , +A n ^A n ⁸      (6)

8 2 n sc     ⁿs0

В диффузионном режиме роста обычно полагают, что ∆ n <<  ∆ n _δ и соответственно n_sс ≈ n_s0.

Тогда выражение (6) упрощается до следующего:

DR

P —----2 An 8- ns08

В кинетическом режиме роста кристалла пересыщение раствора у поверхности кристалла и перепад концентрации в пограничном слое могут принимать разные и независимые друг от друга значения, но в предельном случае ∆ n <<  ∆ n _δ и

DR

P —---- -A n A n ₈ .

ⁿs0 ⁸

Из уравнения баланса вещества получим нормальную скорость роста кристалла

DM A n$ v —--.

P o ⁸

Легко убедиться, что удельное производство энтропии в диффузионном режиме роста кристалла пропорционально квадрату нормальной скорости роста кристалла.

Учитывая, что в рассматриваемую систему включен не весь пограничный слой, а только его линейный участок, а вклад тангенциального потока раство- ра вдоль грaни не рассматривается, результаты расчета производства энтропии по формуле (6) будут незначительно занижены.

Ha основе экспериментальных данных по росту граней октаэдра кристалла алюмокалиевых квасцов в стационарном режиме [4], рассчитано производство энтропии с ростом пересыщения (рис. 4). В частности, при температуре 20° С и абсолютном пересыщении (2∙10–5 моль/л), обычном для условий выращивания кристаллов квасцов, удельное производство энтропии составляет 2∙10–8 Дж/(К∙с∙ᴫ). Для сравнения, в режиме стационарной диффузии вещества в растворе при градиенте концентрации 0.1 моль/(ᴫ∙см) удельное производство энтропии достигает гораздо больших значений — 4∙10–5 Дж/(К∙с∙ᴫ).

3,5

2,5

1,5

0,5

0        0,5        1         1,5        2        2,5        3

A C, 10^-5 моль/л

Pиc. 4. Зависимость удельного производства энтропии при росте грaни (111) алюмокалиевых квасцов от пересыщения

3. Рост кристалла из расплава

Рассмотрим аналогичную задачу для роста кристалла из рaсплава методом Чохральского. Метод Чохральско-го предполагает достижение стационарного режима роста кристаллической були плоским фронтом (рис. 5) [2]. Представим однокомпонентную двухфазную систему. Теплоотвод от растущей поверхности кристалла осуществляется через охлаждаемый кристалл [2]. Перед фронтом кристаллизации в

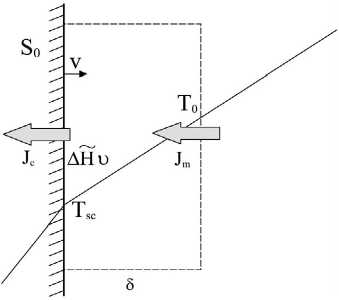
Pиc. 5. Распределение температуры в расплаве у поверхности растущего кристалла расплаве формируется градиент температуры, такой, что поток тепла к кристаллу складывается с теплотой кристаллизации, выделяемой на поверхности роста, и образует поток теплоты, уводимый через кристалл

интегралов, удельное производство энтропии сводится к виду

p'

1 djS

S03 dt

,

u

AH AT 2

m3 !0

~ ДНТ.

As +----^

T02

^ n A , (9) ; TSC

где — разность парциальных молярных энтальпий кристалла и распла-

1 dN ва,          — молярная скорость

Sq dt

роста кристалла.

Выделим систему, включающую поверхность кристалла площадью S₀ с некоторым тонким слоем кристаллического вещества и некоторый объем переохлажденного расплава толщиной δ , такой, что на расстоянии δ от поверхности кристалла температура в расплаве соответствует температуре плавления. Будем перемещать границы системы вместе с фронтом роста. В такой системе диффузией вещества можно пренебречь, и локальное производство энтропии зависит только от диффузии тепла и термического эффекта кристаллизации

где —разность парциальных молярных энтропий кристалла и расплава, ∆ T = T 0 – T sc .

Eсли считать, что ∆ T << T₀, T_sc ≈ T₀, то можно пренебречь одним слагаемым в квадратных скобках и выражение (9) упростить до вида

Pcv

MT0

To

,

a = J 5 f I ^m - Ис) и иах(т) T 5

где J_u — поток плотности внутренней энергии, µ _m, µ _c — химические потенциалы кристаллизующегося соединения в расплаве и кристалле.

При отсутствии диффузионного и конвективного переноса вещества в выделенной системе, поток внутренней энергии можно записать в виде .

Разность парциальных молярных энергий расплава и кристалла связана с разностью химических потенциалов и разностью парциальных молярных энтропий .

Расчет удельного производства энтропии системой производится с помощью нахождения интегралов

p* = Xdis =

S03 dt

1 ^(All+TAs) cT , = - f        —udx +

8p T2 6x

. о 0 1

Eсли учесть термическую зависимость химических потенциалов и произвести необходимые преобразования

где v — нормальная линейная скорость роста кристалла, T ′ — градиент температуры в расплаве перед фронтом роста, ρ _c — плотность кристалла, М — молярная масса.

Таким образом, удельное производство энтропии растущим кристаллом в расчете на единичный объем контактирующего с ним расплава определяется относительно простым выражением. Нормальная скорость роста в первом приближении линейно зависит от скорости теплоотвода и соответственно от градиента температуры, поэтому полученное выражение для удельного производства энтропии закономерно проявляет квадратичную зависимость от нормальной скорости роста, так же как выражение для роста кристалла из раствора в диффузионном режиме. Поскольку анализируемая расплавная термодинамическая система не включает сам кристалл, за исключением его поверхности, то производство энтропии при диффузии тепла в кристалле не вносит вклада в формулу (10).

Таким образом, определение степени неравновесности физико-химической системы зависит от вида формулы, полученной в рамках той или иной модели. Однако во всех случаях степень неравновесности оказывается пропорциональной квадрату скорости реакции (скорости роста кристалла). Остальные физико-химические параметры, входящие в формулу, определяются табличными значениями или условиями опыта. Во всяком случае, используя скорость производства энтропии в качестве меры неравновесности, появляется возможность сравнивать динамику разных процессов, пользуясь единой «шкалой».

Исследования проводились в рамках программы фундаментальных исследований Президиума РАН за 2006 г. «Разработка методов получения химических веществ и создание новых материалов», также поддержаны грантом Президента Российской Федерации НШ.2250.2003.5.