Термодинамическая модель шлакового расплава с произвольным числом сортов катионов и анионов

Жидкие металлургические шлаки в соответствии с их физико-химическим характеристикам относят к категории ионных расплавов [1, 2]. Известно, что главными исходными составляющими металлургических шлаков являются оксиды. Помимо оксидов исходными компонентами шлаков могут являться также фториды, сульфиды и некоторые другие группы соединений, поставляющие в расплав при плавлении различные сорта катионов и анионов.

Термодинамические свойства шлаковых расплавов определяются их составом и температурой. Поскольку диапазон составов промышленных шлаков широк, экспериментальное исследование их термодинамических характеристик представляет сложную задачу. Изучение даже таких относительно простых объектов, как тройные или четверные системы, является трудоемким и длительным. Исследование свойств пяти-, шестикомпонентных и более сложных систем является еще более сложным, поэтому в литературе содержатся сведения о результатах экспериментального изучения лишь их отдельных фрагментов. В условиях значительного дефицита экспериментальной информации [3-5] основные надежды на получение термодинамических данных о сложных по составу жидких шлаках связываются с модельными методами химической термодинамики, опирающимися на экспериментальные данные о свойствах простых систем, и связывающих на основе теоретических положений свойства простых и многокомпонентных расплавов.

В работе [6] было опубликовано описание термодинамической модели оксидного шлакового расплава, содержащего один сорт анионов - анионы кислорода. В основу этой модели были положены представления об островной структуре ионных расплавов, находящихся в условиях относительно небольшого перегрева над температурой ликвидуса [7]. Теоретические положения термодинамической модели сводились к следующему. Структурными составляющими шлакового расплава являются простейшие по составу ионы, сгруппированные в микрокомплексы (островки), имеющие в пределах нескольких координационных сфер кристаллоподобное упорядочение по типу твердых фаз. Островки неупорядочены во взаимном расположении относительно друг друга, являются неустойчивыми короткоживущими динамическими образованиями, связанными друг с другом непрерывным обменом частиц. Эти образования отражают усредненный состав расплава, разрушаясь в одном месте, они возникают в дру гом и поэтому не могут рассматриваться в качестве микро-фаз. Координационные числа катионов в таких микрокомплексах постоянны и по своим величинам близки к координационным числам соответствующих катионов в жидких простых оксидах. Предложенная термодинамическая модель показала свою хорошую эффективность в термодинамических расчетах [8-12]. Это сделало целесообразным расширение области ее применения на более сложные по составу (полианионные) шлаковые расплавы, что и стало задачей данной работы.

Рассмотрим ионный расплав, содержащий к сортов катионов и I сортов анионов. Допустив при образовании расплава полную электролитическую диссоциацию всех исходных компонентов на простейшие катионы и анионы, выразим общее количество катионов (А_кет) и общее количество анионов ( N^ ) в расплаве соотношениями:

^OT=^off^..            (1)

'=1 7=1

^N™-^NoT?L^vy^mu ■               (2)

7=17=1

Здесь N_q - число Авогадро; Vy и Vy - количества катионов и анионов (соответственно), образующихся при диссоциации молекулы компонента (у); ту - числа молей исходных молекулярных компонентов (у) в системе.

Ионные доли катиона произвольного сорта (s) и аниона произвольного сорта (7) в расплаве в этом случае будут определяться уравнениями:

^s ^'^j^'sj^sj /^кат ’(^)

7=1/

Vi^W, Jn^.(4)

Будем считать, что зависимость среднего значения координационного числа катиона сорта (s) в полианионном расплаве z* (равного среднему числу анионов в его ближайшей координационной сфере) от анионного состава расплава характеризуется функцией г5=Х4^7>                    <5)

7=1

в которой величины z* соответствуют значениям координационных чисел катиона сорта (s) в чистых жидких компонентах (s/).

Представим энергию расплава в виде сумы

энергий чистых жидких компонентов и избыточной энергии, характеризующей эффект образования расплава к ! 5 =                                   (6) '=1 7=1 Здесь Еу - молярная энергия чистого жидкого компонента (zy). Появление слагаемого Е”6 будем связывать с двумя главными факторами: различиями в структурах жидких компонентов и зависимостью величин энергий связей между катионами и анионами в расплаве от состава расплава. Число связей катионов сорта (z) в расплаве с окружающими их анионами будем определять соотношением = ЦУит>А4 = HVymijNO U^J ) • <7> 7=1                7=1 Зависимость избыточной энергии связи между катионом сорта (z) и анионом сорта (/) в расплаве от состава расплава опишем с помощью ряда '—1 ( йс.. А         к (Зе-- А U Е         Е -. Хт* m-1 V ^т У    m=z+l к ихт У у-1 ( Зе Л        l „ ( Зе-у +Д^Уп+^ -^Уп-      (8) п=к*1\°Уп ) В суперпозиционном приближении с учетом (7) конфигурационную энергию расплава можно

Перегруппировав выражение (11) и введя дополнительные обозначения, приведем его к виду к 1 E=hh4mu + i=kj=l ( к 1         А /      (к-1 к           . .. А + Т^^^У iyj ЕЕ Х,Хт^т + ч ;=1 у=1      у 7=1 к '=1 т=/+1          У (к 1      А * (м i          А + EEw Ех- Е Е yjy^v) • <12) к'=17=1      У'=1 к7=1"=7+1         У Здесь Г ( 9бц А . (ЭЕт. А 2V0                                 5 _ V^m У    к ^ /_ = No [zy f + zm ( (14) L         1^7 - функции, характеризующие энергии образования бинарных расплавов из жидких молекулярных компонентов (zy) и (иу) (имеющих одинаковый анион сорта у) и бинарных расплавов из жидких молекулярных компонентов (zy) и (ш) (имеющих одинаковый катион сорта z"), a Zy - координационные числа анионов в жидких компонентах (zy). Допустим, что в расплавах с общими анионом сорта у концентрационные зависимости величин Еу и Emj описываются функциями

представить в виде: к 1              к 1 Е = У^ 4тУ + £ Е ^ ™уИ0У^ Еу = t=l J=1           1=1 7=1 £ /      f  к I    Лк1 + ^EE^- УлУ^ [N^s.j} • (9) '=17=1         k '=17=1      У'=1 7=1 Приняв во внимание, то что EE^4 =ЕЕк2'к         0°) '=1 7=1          ,=1 7=1 выражение (9) с учетом (2) и (8) преобразуем к виду к 1            (     к 1         ' E = TiLEymy+ КоЕ^уМу х '=17=1          V    '=17=1       У 1 Г * >-i           (ds Л хУ у. У У x.xmNQz*j —У- + ' J 1—11—! 1 т У у 7=1 L'=lm=l          \ихт J к '-1           ( 5е ,Л1 ( к 1      Ai ^У.Х>ХтМ02у J + ^Т^У^У Xх'Х /=1 m=l          k^myj V   /=17=1      у/=1 / j"^            ( Эе х mLyjynN0Zy + 7=1 и=1           Х^Уп ) i 1            (Se\                    - ^^УуУАху -У- .            (11) 7=1л=7+1           Х^Уп

Еу=^/хт+ЬУ,х1хт,                (15) Emj =<^Рх1*Ь^Х,Хт,                 (16) а в расплавах с общим катионом сорта z функциями Еу=а'^уп+Ь^УуУ„,                  (17) £у = а^+Ь(^у»’              (18) в которых параметры а^ , Ь^, а'^, Ь^ являются энергетическими константами. Подставив (15), (16) в (13), а (17), (18) в (14) и проведя дифференцирование, получим ^’ = е^+(4 - 4,)-(^ -».)^’.    (I?) “fi-e^-^lk-*  (20) Здесь ^=Н^<^*^^,      (21) ^^^(z^ + z,;^),          (22) ^=N^,               (23) qJ^=N<                    (24) - энергетические параметры модели. Введя в рассмотрение функцию состава расплава

Власов В.Н.

k I            / к I

^=УХ^у>_ч Т3>у^ту> '=1 7=1       / 7=17=1

совершенного ионного раствора, а 5юб - избы

равную отношению общего числа молей катионов к общему числу молей анионов в расплаве, с учетом записанных выше соотношений получим выражения для энергии расплава и парциальной молярной энергии произвольного компонента (sf) в

точная энтропия смешения жидких компонентов.

Поскольку теплоемкость шлакового расплава

примерно соответствует аддитивно сложенным теплоемкостям чистых жидких компонентов, будем считать слагаемые 8^го и 5^й36 независящими от температуры и являющимися лишь функциями

расплаве.

состава расплава.

Энтропия образования совершенного ионного

7=1 7=1

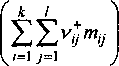
^j=\   /=1 m=i+l

раствора определяется произведением чисел случайных перестановок катионов друг с другом и анионов друг с другом. Ее концентрационная зависимость характеризуется формулой

к-\ к

+ Е Е Х-Хт

z=l m=z+l

+7fE^E Е ъ^б +

*<7=1   7=177=7+1        '

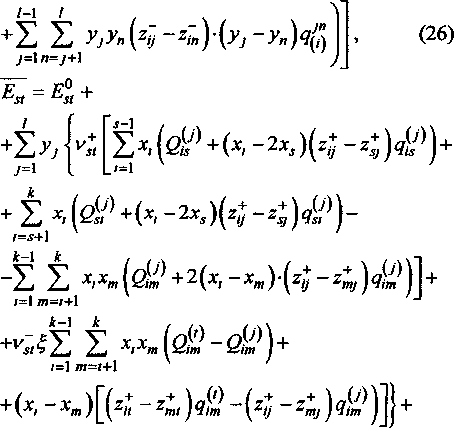
к _ /-1     ,                                           ,

+2> N Е^ +(^7 -²Wy -wb)⁺

+ Е ^ (% Чу к ~²уДу ДД”

j=t+i

~Ё Е У,У»^+Цу,-УпЧ

J=ln=J+i

“(^^^А+уЁ Е уДе^-е(^+

* 7=1 ”=7+1

⁺(-Ъ ~У^п)^25к^-2₅п)9($)^-Чу ^-z”v)^) |- ^7)

Энтропию расплава выразим соотношением

S^^my+s^+S™6,        <28>

7=1 7=1

в котором: Sy - молярная энтропия чистого жид кого компонента (у), 8ВД - энтропия образования

S^-R

к ( 1

Ё 1>у^ту

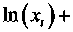
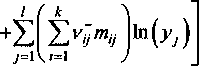
Концентрационную зависимость избыточной

энтропии смешения представим в виде уравнения

к-1 к

⁺Е Ё ^Х.^Хт

7=1 777 =7+1

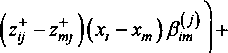
+у(Е^ Ё Е УкУп«^

* <7=1   7=177=7+1

+Е Е УкуД-Дук-уЧ^ - 7=177=7+1                                у

в котором а^, р^, а/л , р^ являются посто

янными величинами (энтропийными параметрами модели).

Воспользовавшись зависимостями (29) и (30) проведя дифференцирование уравнения (28) по числу молей произвольного компонента (sZ) получим выражение для парциальной молярной энтропии компонента, ^ = 5° +

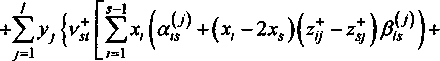
+ Е ^х< Д⁺V^х. - ^2xJ(4 - 4l^) ” J=S+1 t-i к ,

-Z E ^X-^Xm\«im +2(x,-X_m)x 7=1 777=7+1

A^Zy ” ^zmj ^im )] + ^X.^Xm ^ ~ 4m ) + ⁺U -^xm)[(4 -Д4т 4^zy -2^)44) ) +

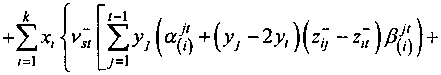
+ Е И) +к ~2У«Х2и -^И))- у=/+1

~Ё Z VjVn («g *4? j ^z7n^S+ J=\n=j*\                                         ^J

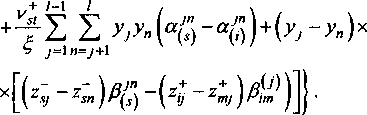
Используя уравнения (27) и (31) несложно перейти к выражению для химического потенциала произвольного компонента (st) в шлаковом расплаве

^^~^> (32)

а также к выражению для его активности

^)=ехр:

трИЗб т _сИЗб

RT

Термодинамическая модель шлакового рас плава с произвольным числом сортов катионов и анионов, предложенная в данной работе, сохраняет все основные достоинства опубликованной ранее [6] модели оксидного шлака. Полученные термодинамические зависимости связывают свойства простых и неограниченно сложных по составу систем, обладают хорошими интерполяционными возможностями, разумной гибкостью, изменяющейся в зависимости от структуры и природы исходных компонентов расплава. В силу указанных обстоятельств выведенные соотношения могут найти практическое применение в термодинамических исследованиях, направленных на обобщение и дополнение имеющейся информации о свойствах шлаковых расплавов, моделировании термодинамических характеристик жидких шлаков, а также в расчетах высокотемпературных равновесий в системах с их участием.

Выводы

• 1.    С учетом ионной природы жидких шлаков на основе островной модели строения ионных жидкостей разработана термодинамическая модель шлакового расплава, содержащего произвольное число сортов катионов и анионов.

• 2.    Выведены уравнения для основных термодинамических характеристик жидких шлаков (энтальпии и энтропии образования расплавов, парциальных молярных свойств компонентов, активности компонентов), выражающие их зависимость от состава и температуры системы.

• 3.    Полученные соотношения связывают свойства простых и сложных по составу ионных рас

плавов, обладают хорошими интерполяционными возможностями и могут найти практического применения в термодинамических исследованиях.