Термодинамические аспекты изменения электрической проводимости полиэтилена высокой плотности, наполненного технической сажей

DOI:

Результаты и обсуждение

Авторы работы [12] обнаружили зависимость коэффициента диффузии D водных паров от температуры стеклования Т _с для дисперсно-наполненных композитов поливинилаце-тат/двуокись титана (ПВАц/TiO₂), а именно снижение D по мере повышения Т _с. Повышению Т _с по мере роста содержания наполнителя авторы публикации [12] дали частное объяснение, предположив, что этот эффект обусловлен адсорбцией ацетатных радикалов на поверхности частиц наполнителя и разрушением межцепных водородных связей. Однако указанный эффект имеет общий характер и наблюдается не только для композитов, но и для ненаполненных полимеров. Так, в статье [2] обнаружено систематическое снижение D по мере роста Т _с для ряда полимеров, которое объяснено увеличением кинетической жесткости цепи по мере повышения Т _с. Авторы работы [10] аналогичный эффект объяснили изменением свободного объема полимеров. Целью настоящей работы является структурный анализ изменения коэффициента диффузии по мере повышения содержания наполнителя для композитов ПВАц/TiO₂.

Эксперимент

В качестве матричного полимера использован сополимер поливинилхлорид-винилацетат (ПВАц), содержащий 87 % винилхлорида и 13 % винилацетата, со средневесовой молекулярной массой 10500. Он был поставлен фирмой «Union Carbide Chemicals Comp». В качестве наполнителя использована двуокись титана (TiO2) с чистотой ~ 97 %. Размер исходных частиц варьировался в пределах 70–400 нм при средней величине 200 нм. Материал поставлен фирмой «du Pont de Nemours and Comp.» [12].

Пленочные образцы композитов ПВАц/ TiO2 толщиной ~ 0,1 мм и с содержанием наполнителя 3,38–42,56 масс. % получены из раствора в смеси метилэтилкетона, метилизобу-тиленкетона и ксилена. Диффузионные характеристики рассчитывались по растворимости водных паров в исследуемых композитах на весах Макбейна – Бакра двумя способами. Температура стеклования композитов определена дилатометрическим методом [12].

Авторы статьи [10] предложили следующее уравнение, описывающее зависимость коэффициента диффузии D от температуры стеклования Т _с:

lg D = –(3,44 + 0,013 T _c ). (1)

Поскольку уравнение (1) является эмпирическим, то для его корректного применения к рассматриваемым композитам с учетом разных единиц для D , используемых в работах [12] и [10], постоянный коэффициент 3,44 в указанном уравнении был заменен на 1,38, и затем модифицированное таким образом соотношение было использовано для теоретической оценки коэффициента диффузии. На рисунке 1 приведено сравнение полученной экспериментально и рассчитанной согласно модифицированному уравнению (1) зависимостей D от объемного содержания ф _н наполнителя для рассматриваемых композитов. Как можно видеть, получено хорошее как качественное (расчет согласно предложенному уравнению адекватно описывает экстремальный характер зависимости D ( ф _н)), так и количественное (среднее расхождение теории и эксперимента составляет ~ 18 %, что типично для оценок коэффициента диффузии [3]) соответствие рассчитанных и экспериментальных результатов.

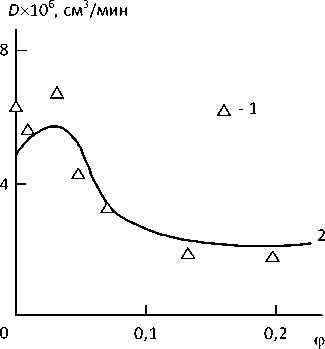
Рис. 1. Сравнение полученной экспериментально ( 1 ) и рассчитанной согласно модифицированному уравнению (1) ( 2 ) зависимостей коэффициента диффузии водных паров D от объемного содержания наполнителя ф для композитов ПВАц/TiO₂

Рассмотрим структурные основы изменения температуры стеклования и, следовательно, коэффициента диффузии для исследуемых композитов. В работе [4] было показано, что повышение относительной доли плот-ноупакованных областей структуры полимерных материалов приводит к линейному росту температуры стеклования. В случае композитов относительная доля плотноупакованных областей ф _пл определяется следующим образом [5]:

Ф пл = Ф кл + Ф н + Ф мф ,          (2)

где Ф кл , Ф н и Ф_м ф — относительные доли областей локального порядка (нанокластеров) в полимерной матрице, наполнителя и межфазных областей соответственно.

Величина ф _кл рассчитана согласно следующему перколяционному соотношению [4]:

Ф кл =0,03( т с - Т ) 0,55 ,            (3)

где Т – температура испытаний, принятая равной 293 К.

Суммарная величина ( ф _н + Ф мф ) определяется следующим образом [6]:

( Ф н⁺ Ф мф ) = Ф н^{(1+ cb} а⁾ ,         ⁽⁴⁾

где с – постоянный коэффициент, равный ~ 1,2 для дисперсных частиц; b _а - безразмерный параметр, характеризующий уровень межфазной адгезии, полимерная матрица-наполнитель, который определяется с помощью уравнения [8]:

б , = б : ^м - ь б ( б : ^м - б т ) ,                 (5)

где б _к ,б ^с _к ^м и б ^Т _к – коэффициенты теплового линейного расширения композита, определенные экспериментально и рассчитанные согласно правилу смесей и уравнению Тернера соответственно.

Величина б ^с _к ^м определяется следующим образом [8]:

б ^с; = б м ( 1 - ц н ) + б „ ц „ ,              (6)

где ам и ан - коэффициенты теплового линейного расширения матричного полимера и наполнителя соответственно: ам = 6,5 х 10-5 К-1, ан= 0,27 х 10-5 К-1

Правило (6) справедливо только для идеального случая, когда каждая фаза полимерного композита расширяется независимо друг от друга. Уравнение Тернера имеет следующий вид [8]:

Т = бм (1 - Цн)Км + б„ц„Кн 1:      (1 - цн) Км + цн Кн где Км и Кн – объемные модули полимерной матрицы и наполнителя соответственно.

При замене величин К _м и К _н в уравнении (7) на соответствующие значения модуля Юнга Е _м и Е _н указанное уравнение дает предельные значения а _: , которые соответствуют совершенной адгезии по Кернеру [8]. Параметр b _а позволяет не только количественную, но и качественную градацию уровня межфазной адгезии в полимерных композитах. Так, условие б _: = б : ^м, то есть независимое тепловое расширение фаз полимерного композита, возможное только при отсутствии адгезии между ними, реализуется при b _а = 0. Условие б _: = б Т , или совершенная адгезия по Кернеру, реализуется при b _а = 1,0. И, наконец, критерий b _а > 1,0 определяет реализацию эффекта наноадгезии [6].

На рисунке 2 приведена зависимость Т с ( ф _н) для рассматриваемых композитов, которая показала линейный рост Т _с по мере увеличения Ф _н и описывается следующим эмпирическим уравнением:

Т с =100 ф _н + 293, К. (8)

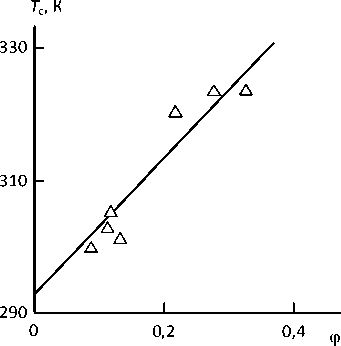
Рис. 2. Зависимость температуры стеклования Т _с от относительной доли плотноупакованных областей структуры ф для композитов ПВАц/TiO₂

Такое же уравнение для оценки величины Тс получили авторы работы [5] в случае дисперсно-наполненных композитов полигид-роксиэфир/графит. Это обстоятельство подтверждает общность уравнения (8) и позво- ляет сделать вывод, что максимальное повышение температуры стеклования, по крайней мере, для дисперсно-наполненных полимерных композитов, не может превышать 100 К при ϕпл=1,0.

Сравнение уравнений (1) и (8) демонстрирует, что изменение коэффициента диффузии композитов ПВАц/TiO₂ обусловлено ростом содержания плотноупакованных областей их структуры. Этот постулат полностью соответствует выводам работ [2; 10]. Так, известно [4], что весь свободный объем полимерного материала концентрируется в рыхло-упакованных областях его структуры, относительную долю которых ϕ _р.м можно определить следующим образом [4]:

ϕ _р.м= 1 – ϕ _пл. (9)

Увеличение ϕ пл приводит к снижению ϕ р.м и, соответственно, к уменьшению относительной доли свободного объема. Кинетическую жесткость полимерной цепи можно охарактеризовать фрактальной размерностью D _ц участка этой цепи между точками ее фиксации, которая определяется с помощью уравнения [6]:

• ² = С ∞ ^{D ц} , (10) ц пл

где С _∞ – характеристическое отношение.

Из уравнения (10) следует, что при С _∞ = const увеличение ϕ пл приведет к снижению D _ц или повышению кинетической жесткости полимерной цепи.

И в заключение оценим минимальную величину коэффициента диффузии D _min для рассматриваемых композитов. Из уравнения (8) при ϕ _пл= 1,0 получим Т _с= 393 К и, согласно модифицированному уравнению (1), D _min = 0,324 см²/мин, что на порядок ниже значения D для матричного полимера.

Выводы

Таким образом, результаты настоящей работы продемонстрировали зависимость коэффициента диффузии полимерных композитов от их температуры стеклования. В свою очередь, указанная температура и, следовательно, коэффициент диффузии определяются относительной долей плотноупакованных областей структуры полимерного композита, что согласуется с предложенными ранее концепциями. Рассмотренная модель позволяет оценить предельные значения как температуры стеклования, так и коэффициента диффузии композитов поливинилацетат/двуокись титана.