Термодинамический анализ фазовых равновесий при раскислении хромсодержащих сталей марганцем и цирконием

Макровец Лариса Александровна; Михайлов Геннадий Георгиевич; Выдрин Дмитрий Александрович; Makrovets Larisa Alexandrovna; Mikhailov Gennady Georgievich; Vydrin Dmitry Alexandrovich

Термодинамический анализ фазовых равновесий при раскислении хромсодержащих сталей марганцем и цирконием

Автор: Макровец Лариса Александровна, Михайлов Геннадий Георгиевич, Выдрин Дмитрий Александрович

Журнал: Вестник Южно-Уральского государственного университета. Серия: Металлургия @vestnik-susu-metallurgy

Статья в выпуске: 15 (274), 2012 года.

Бесплатный доступ

Рассмотрены термодинамические особенности процессов взаимодействия кислорода, хрома, марганца, углерода и циркония в жидком железе. Рассчитана диаграмма состояния Cr 2O 3-MnO-ZrO 2 и подобраны параметры субрегулярной теории для жидких и твердых растворов на основе оксида циркония. Построены поверхности растворимости кислорода в жидком металле системы Fe-Cr-Mn-Zr-O-C. Изучено влияние температуры на раскислительную способность марганца и циркония в жидкой хромсодержащей стали. Результаты работы могут быть использованы при разработке технологии рафинирования стали сплавами и лигатурами, содержащими цирконий.

Цирконий, фазовые диаграммы, фазовые равновесия, термодинамическое моделирование

Короткий адрес: https://sciup.org/147156723

IDR: 147156723 | УДК: 536.7:669.15

Thermodynamic analysis of phase equilibria in chromium steels deoxidized with manganese and zirconium

The thermodynamic features of the interaction of oxygen, chromium, manganese, zirconium, and carbon in liquid iron are considered. The Cr 2O 3-MnO-ZrO 2 phase diagram and subregular theory parameters for liquid and solid solutions based on zirconium oxide are calculated. Oxygen solubility surfaces in the liquid metal of the Fe-Cr-Mn-Zr-O-C system are calculated. The influence of temperature on the deoxidizing ability of manganese and zirconium in liquid chromium steel is investigated. Results can be used in developing a technology of refining steel with alloys containing zirconium.

Текст научной статьи Термодинамический анализ фазовых равновесий при раскислении хромсодержащих сталей марганцем и цирконием

Значительный интерес к использованию циркония при выплавке как сплавов специального назначения, так и марганцовистых и хромистых сталей был вызван развитием атомной энергетики. При вводе циркония в металл отмечается повышение теплостойкости, улучшение обрабатываемости и свариваемости, измельчение первичного зерна, модифицирование неметаллических включений стали и сплавов. Однако литература по вопросам раскисления цирконием даже конструкционных сталей ограничена. Представляет интерес термодинамический анализ процессов взаимодействия циркония, введенного в сталь, с кислородом в присутствии других элементов, например, хрома, марганца и углерода.

Для проведения термодинамического анализа процессов взаимодействия марганца, хрома и циркония с кислородом использована теория субрегулярных ионных растворов в приближении о квадратичной от состава зависимости энергий смешения [1]. Предварительный анализ показал, что при концентрациях марганца, хрома и циркония в стали, представляющих интерес, состав неметаллический включений определяется сопряженной с об- ластью существования металлических расплавов системой Cr2O3–MnO–ZrO2 . Активности компонентов оксидного расплава рассчитываются по теории субрегулярных ионных растворов, в частности, для этого трехкомпонентного расплава имеют вид [1]:

lg a ( Cr₂o₃ ) = 2lg ^X 1 ⁺ 2lg Y i = 2lg ^X 1 ⁺ ² [ З x i ² ^X 2 6 1112 ⁺

+ x x 2² ( 2 - 3 x j ) 6 1 122 ⁺ ^X 2 ⁽ ^{1 3} ^X 1 ) 6 1222 ⁺

⁺ ³ ^X 1 x 3 ⁽ ¹ ^— ^X 1 ) 6 1113 ⁺ ^X 1 ^x 3 ⁽ ² - ³ ^X 1 ) 6 1133 ⁺

⁺ ^X 3 ⁽ ¹ - ³ ^X 1 ) ⁶ 1333 - ³ ^XI^X 3 ⁽ ¹ - ^X 1 ) Q 2223 ^— ³ ^X 2 ^X 3 Q 2233 ^—

^— ³ ^X 2 ^X 3 ⁽ ¹ - ³ ^X 1 ) ⁶ 2333 ⁺ ^X 1 ^X 2 ^X 3 ⁽ ² - ³ ^X 1 ) Q 1123 ⁺

+ X 2 X 3 ( 1 - 3 X 1 ) 6 1223 + X 2 X 3 ² ( 1 — 3 X 1 ) 6 1233 ] /( 2 3 RT ) ; (1)

^lg a ( MnO ) = ^lg ^X 2 ^{+ [} ^X 1 ⁽ ¹ ^- ³ ^X 2 ) ⁶ 1112 ⁺

⁺ ^X 1 ^X 2 ( ² ^— ³ ^X 2 ) ⁶ 1122 ⁺ ³ ^X 1 ^X 2 ( 1 ^— ^X 2 ) ⁶ 1222 ^—

^- ³ ^X 1 ^X 3 ⁶ 1113 ^— ³ ^X 1 ^X 3 ⁽ ² ^— ³ ^X 1 ) ⁶ 1133 ^— ³ ^X 1 ^X 3 ⁶ 1333 ⁺

⁺ ³ ^X 2 ^X 3 ⁽ ¹ ^— ^X 2 ) ⁶ 2223 ⁺ ^X 2 ^X 3 ⁽ ² ^— ³ ^X 2 ) ⁶ 2233 ⁺

⁺ ^X 3 ⁽ ¹ ^— ³ ^X 2 ) ⁶ 2333 ⁺ ^X 1 ^X 3 ⁽ ¹ ^— ³ ^X 2 ) ⁶ 1123 ⁺

⁺ % i x 2 x 3 ⁽ 2 ^— 3 x 2 ) Q 1223 ⁺

+ X i x 3 ² ( 1 - 3 x 2 ) Q 1233 ] /( 2,3 RT ) ; (2)

lg a ( ZrO₂ ) = lg ^X 3 ⁺ [^- ³ ^X 3 ^X 2 Q 1112 - ³ ^X1 ^x 2 Q 1122 ^-

- 3 ^X 1 x 2 Q 1222 ⁺ ^X 1 ⁽ ¹ - ³ ^x 3 ) Q 1113 ⁺ ^X 1 ^x 3 ⁽ ² - ³ ^x3 ) Q 1133 ⁺

+ 3 ^X 1 ^x 3 ⁽ ¹ ^- ^x 3 ) ^Q1333 ⁺ ^x 2 ⁽ ¹ ^- ³ ^x 3 ) ^Q 2223 ⁺

⁺ ^x 2 ^x 3 ⁽ ² ^- ³ ^x 3 ) ^Q 2233 ⁺ ³ ^x 2 ^x 3 ⁽ ¹ ^- ^X 1 ) ^Q2333 ⁺

⁺ ^X 1 ^x 2 ⁽ ¹ ^- ³ ^x 3 ) ^Q1123 ⁺ ^X 1 ^x 2 ^x3 ⁽ ² ^- ³ ^x 2 ) Q 1223 ⁺

+ X 1 X 3 ² ( 1 - 3 X 2 ) Q 1233 ] /( 2,3 RT ) , (3)

где x 1 , x 2 , x 3 – ионные доли катионов Cr 3+ , Mn²⁺ , Zr⁴⁺ в оксидном расплаве, Q_ijkl – энергетические параметры теории.

По аналогичным формулам рассчитывали активности компонентов твердого раствора Cr₂O₃, MnO, ZrO₂. Параметры теории субрегулярных ионных растворов для твердых растворов подставляли в формулы (1)-(3) в виде Q ijkl .

В таблице приведены энергетические параметры теории субрегулярных ионных растворов для твердых (Qijkl) и жидких (Qijkl) растворов системы FeO –Cr2O3–MnO–ZrO2 . Двойные оксидные диаграммы исследованы ранее [2–4]. В литературе приведено ограниченное число тройных диаграмм состояния с ZrO2, чаще всего есть только упоминание о наличии соединений и твердых растворов, а сами диаграммы не приводятся. Поэтому по информации, основанной на свойствах бинарных оксидных систем, были рассчитаны ранее диаграммы состояния тройных систем FeO–ZrO2–MnO [2] и FeO –ZrO2–Cr2O3 [3].

На рис. 1 приведена расчетная модель диаграммы состояния системы Cr2O3 – MnO –ZrO2 . В соответствии с этой диаграммой в равновесии с жидким металлом могут находиться фазы: кристаллический Cr2O3, MnCr2O4 с незначительной примесью FeO , MnO с незначительной примесью FeO , твердые растворы на основе ZrO2 и оксидный расплав (FeO , Cr2O3, MnO , ZrO2 ) переменного состава с незначительным количеством CrO.

На рис. 2, а, б приведены поверхности растворимости компонентов в жидком металле (ПРКМ) системы Fe–Cr–Mn–Zr–O, построенные по методикам, опубликованным в монографии [1]. Твердые растворы оксидов FeO, MnO и шпинелей

Энергетические параметры субрегулярной ионной теории для системы FeO - Cr2O3 - MnO - ZrO2

Система	Параметры теории, Дж/моль·К
FeO –Cr₂O₃	Q 1112 = –10 500	Q 1122 = –21 000	Q 1222 = –10 500
FeO –Cr₂O₃	Q 1112 = ⁰	Q ₁₁₂₂ = 0	Q ₁₂₂₂ = 0
FeO–MnO	Q ₁₁₁₃ = 0	Q ₁₁₃₃ = 0	Q ₁₃₃₃ = 0
FeO–MnO	Q ₁₁₁₃ = 0	Q ₁₁₃₃ = 0	Q ₁₃₃₃ = 0
FeO –ZrO₂	Q 1114 = 13 550	Q ₁₁₄₄ = 7000	Q 1444 = 27 100
FeO –ZrO₂	Q 1114 = 3684	Q ₁₁₄₄ = 73 680	Q ₁₄₄₄ = 36 840
Cr₂O₃ – MnO	Q ₂₂₂₃ = 0	Q ₂₂₃₃ = 0	Q ₂₃₃₃ = 0
Cr₂O₃ – MnO	Q ₂₂₂₃ = 0	Q ₂₂₃₃ = 0	Q ₂₃₃₃ = 0
Cr₂O₃ – ZrO₂	Q 2224 = 5370	Q 2244 = 33 700	Q ₂₄₄₄ = 27 600
Cr₂O₃ – ZrO₂	Q ₂₂₂₄ = 68 650	Q ₂₂₄₄ = 137 300	Q ₂₄₄₄ = 68 650
MnO –ZrO₂	Q 3334 = –48 780	Q ₃₃₄₄ = –81 260	Q 3444 = –2393
MnO –ZrO₂	Q 3334 = 48 275	Q 3344 = 61 725	Q 3444 = 13 450
FeO–Cr₂O₃–MnO	Q ₁₁₂₃ = 0	Q ₁₂₂₃ = 0	Q ₁₂₃₃ = 0
FeO–Cr₂O₃–MnO	Q ₁₁₂₃ = 0	Q ₁₂₂₃ = 0	Q ₁₂₃₃ = 0
FeO–Cr₂O₃–ZrO₂	Q 1124 = 62 760	Q 1224 = 62 760	Q ₁₂₄₄ = 83 680
FeO–Cr₂O₃–ZrO₂	Q 1124 = 146 450	Q ₁₂₂₄ = 167 400	Q ₁₂₄₄ = 209 200
FeO–MnO–ZrO₂	Q 1134 = –41 840	Q 1334 = 125 500	Q 1344 = 62 760
FeO–MnO–ZrO₂	Q 1134 = 20 920	Q 1334 = 125 500	Q ₁₃₄₄ = 209 200
Cr₂O₃–MnO–ZrO₂	Q ₂₂₃₄ = 0	Q ₂₃₃₄ = 0	Q ₂₃₄₄ = 0
Cr₂O₃–MnO–ZrO₂	Q ₂₂₃₄ = 167 400	Q 2334 = 334 400	Q 2344 = 167 400

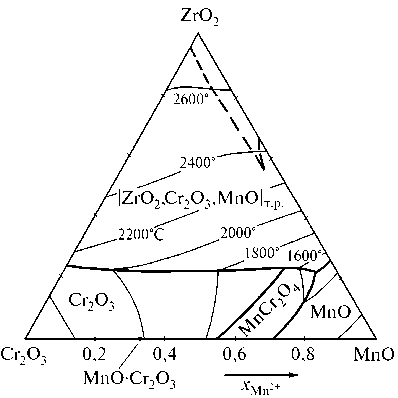
Рис. 1. Расчетная модель диаграммы состояния системы Cr2O3 - MnO - ZrO2

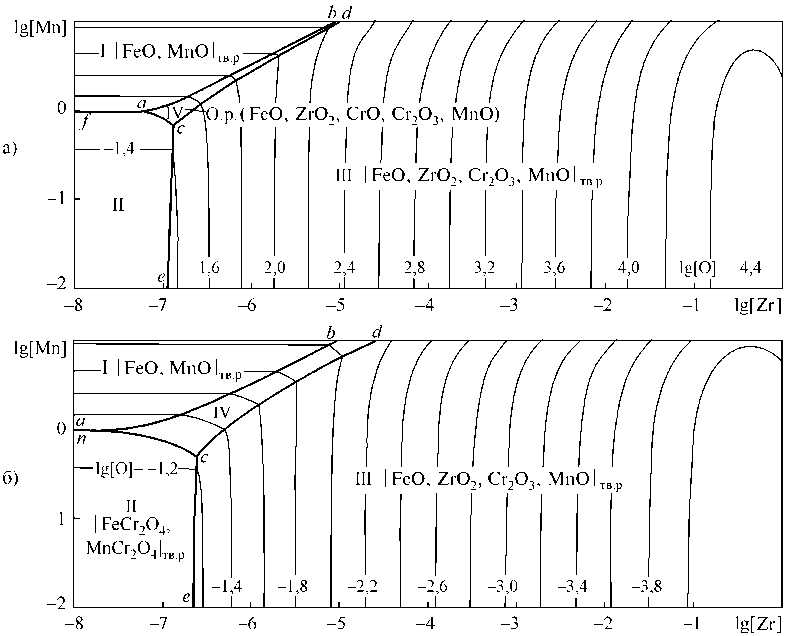
Рис. 2. ПРКМ системы Fe–Zr–Cr–Mn–O при 1873 K, [Cr] = 0,6 мас. %: а) Т = 1550 °С; б) Т = 1600 °С

FeCr2O4, MnCr2O4 при расчете координат ПРКМ считали совершенными растворами, активности компонентов этих растворов приравнивали мольным долям. Активности компонентов оксидного расплава и твердого раствора на основе ZrO2 (FeO , Cr2O3, MnO , ZrO2 ) рассчитывали по теории субрегулярных ионных растворов [1]. В связи с отсутствием надежных экспериментальных данных активность CrO в оксидном расплаве опреде- ляли как в совершенном ионном растворе, то есть приравнивали ионной доле Х(C 2+).

На ПРКМ заданы области составов металла, равновесного с различными оксидными фазами. Жидкий металл, состав которого попадает на определенный участок поверхности, находится в равновесии с неметаллической фазой, указанной в этой области. Например, в области I заданы составы жидкого металла, равновесного с твердыми

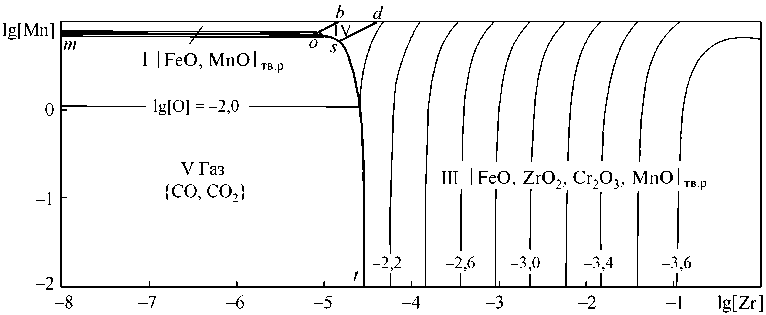
Рис. 3. ПРКМ системы Fe–Zr–Cr–Mn–O–C при 1873 К, [Cr] = 0,6 мас. %, [C] = 0,3 мас. %, P _общ = 1 атм

растворами оксидов FeO, MnO . Если состав металла попадает на границу двух участков, то металл находится в равновесии с двумя неметаллическими фазами. Например, на линии ab заданы составы металла, равновесного с твердым раствором оксидов FeO, MnO и оксидным расплавом. Тонкими линиями показаны сечения поверхности растворимости плоскостями постоянной концентрации кислорода в металле.

Из вида ПРКМ, построенной при [Cr] = = 0,6 мас. % (см. рис. 1), следует, что равновесие с кристаллическим Cr2O3 не реализуется. Область составов металла, равновесного с жидкой оксидной фазой, развита крайне незначительно. При реальных концентрациях циркония в металле (порядка десятых долей процента) в равновесии с жидким металлом могут находиться только твердые растворы на основе ZrO2 .

На рис. 3 приведены результаты расчетов фазовых равновесий для изучаемой системы в присутствии углерода (0,3 мас. %). Видно, что в этом случае возможно лишь образование в равновесии с металлом твердых неметаллических фаз.

Выводы

1. В результате термодинамического анализа установлены энергетические параметры как для жидких, так и для твердых оксидных растворов на основе ZrO₂ .
2. Установлено влияние температуры (1550 и 1600 °С) и содержания углерода (0,3 мас. %) на
3. В связи с высокой химической активностью циркония при модифицировании стали цирконием следует предварительно раскислять сталь присадками сильных раскислителей (алюминием или кальцием).

последовательность фазовых превращений при раскислении хромсодержащей стали марганцем и цирконием.

Список литературы Термодинамический анализ фазовых равновесий при раскислении хромсодержащих сталей марганцем и цирконием

Михайлов, Г.Г. Термодинамика металлургических процессов и систем: моногр./Г.Г. Михайлов, Ю.С. Кузнецов, Б.И. Леонович. -М.: Изд. Дом МИСиС, 2009. -520 с.
Михайлов, Г.Г. Термодинамика процессов взаимодействия кислорода, марганца и циркония в жидком железе/Г.Г. Михайлов, С.В. Свердина, Л.А. Чернова//Производство стали и ферросплавов. Теория и практика: юбилейный сб. науч. тр. -Челябинск: Изд-во ЮУрГУ, 1998. -С. 91-99.
Михайлов, Г.Г. Термодинамика процессов взаимодействия кислорода, хрома и циркония в жидком железе/Г.Г. Михайлов, С.В. Свердина, Л.А. Чернова//Изв. вузов. Черная металлургия. -2000. -№ 1. -С. 4-6.
Михайлов, Г.Г. Термодинамика процессов взаимодействия хрома, марганца и кремния с кислородом в жидком железе/Г.Г. Михайлов, Л.А. Чернова//Высокотемпературные расплавы. -1995. -№ 1. -С. 27-35.