Термодинамический анализ и фазовые равновесия в системе железо-хром-углерод

При термодинамическом анализе фазовых равновесий в трехкомпонентной системе Fe-Cr-C, необходимо знать свойства веществ, образующихся в двухкомпонентных системах железо-хром, железо-углерод и хром-углерод.

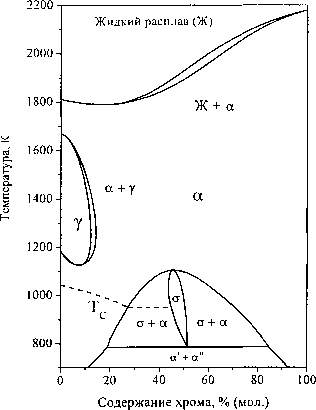
Термодинамический анализ системы железохром проведен в исследованиях [1, 2]. Установлено соответствие расчета и экспериментально определенного минимума линии ликвидуса при концентрации хрома ~17 мол. % и температуре 1516 °C. Хром стабилизирует о.ц.к. модификацию железа и образует с a-железом непрерывный ряд твердых растворов. Область твердых растворов хрома в г.ц.к. модификации железа сравнительно узкая и простирается до концентрации хрома ~14 % (мол.). Хром снижает температуру полиморфного а<^у превращения железа с 910 °C до ~850 °C при содержании хрома ~8,0 % (мол.) (рис. 1, а). При температуре ниже ^1100 К возможно образование упорядоченной сигма-фазы (а).

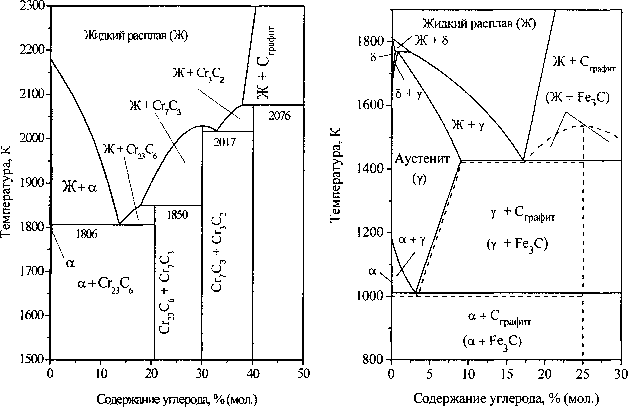
В системе железо-углерод в зависимости от температуры и концентрации углерода стабильными являются следующие фазы: феррит (а, 5), аустенит (у), жидкий расплав (Ж). Термодинамический расчет диаграммы состояния Fe-C выполнен в ряде исследований [3-5]. Диаграмма состояния этой системы представлена на рис. 1, б.

При взаимодействии хрома и углерода воз можно образование карбидов различного состава и структурного типа Сг23С6, Сг7С3 и Сг3С2. Диаграмма состояния системы хром-углерод (рис. 1, в) рассчитана по термодинамическим данным, приведенным в работе [6]. Из вида этой диаграммы следует, что в системе имеют место два эвтектических и два перитектических превращения, приводящих к выделению из жидкого расплава тугоплавких карбидов хрома различного состава.

Система железо-хром-углерод была предметом многочисленных экспериментальных и теоретических исследований [7-9]. Установлено, что в этой системе образуются трехкомпонентный жидкий раствор и тройные твердые растворы внедрения структуры о.ц.к. (феррит) и г.ц.к. (аустенит). Взаимодействие компонентов растворов приводит к образованию карбидов хрома и железа состава М3С, М7С3, М23Сб и Сг3С2, где М = Fe, Сг - компоненты металлической подрешетки.

Жидкий расплав. Молярная энергия Гиббса гомогенного трехкомпонентного сплава задается уравнением

а)

б)

Рис. 1. Диаграммы состояния двухкомпонентных систем: Fe-Cr (а), Сг-С (б), Fe-C (в)

где x_t - молярные доли компонентов раствора; Ly - температурно-зависимые параметры модели, значения которых выражаются полиномами Ред-лиха-Кистера:

zv=4+4(x/-x7)+4(x/-x/)2. (2)

Парциальные молярные энергии Гиббса (химические потенциалы) могут быть вычислены по уравнению [10, 11]

из данных, приведенных в таблице. Параметры L вычисляются по формуле (2), а состав твердого раствора определяется мольными долями веществ в каждой подрешетке:

Ж = W(1 ”^с) иуРе + № = 1;

Ус = (я/фс/( 1 - ^с) и Ус + У У ⁼ 1 •           (7)

В уравнении (5) в подстрочных индексах запятая разделяет компоненты в одной подрешетке, а

G,=H,=Gm + Z(4

7=2

9G_m OX,

Ч

двоеточие означает различие подрешеток.

Парциальные молярные энергии Гиббса гипо

где бу - символ Кронекера (S у = 0 при г ^ j и

тетических компонентов твердого раствора определяются следующим образом [12]:

Ьу= \ при / = у).

Значения параметров модели приведены в таблице.

О.ц.к. и г.ц.к. - твердые растворы внедрения. В таких растворах металлические вещества (железо и хром) образуют подрешетку замещения, а углерод и вакансии (V) - подрешетку внедрения. Тогда такой твердый раствор внедрения можно представить общей формулой (Сг,ГеХ(С,Р)_с. В случае г.ц.к.-фазы а = с = 1, для о.ц.к.-фазы а = 1 и с = 3. Образование такого раствора можно также представить смешением гипотетических соединений Ст_аС_с, Сг_аУ_С1 Бе_аС_с и ¥е_аУ_с, тогда молярная энергия Гиббса такого «четырехкомпонентного» раствора может быть задана уравнением

^т - УСгУу^СгУ ⁺ УСтУс^Сг.С ⁺ УреУу^РеУ ⁺

+У?еУс^СУ.С ⁺ ЯЛ^а(Ж ¹¹¹ Ж + Уре ^1п Ж ) ⁺

+c(y_c\ny_c+y_v\ny_v) + G”⁶ +G^,      (4)

где

^ ' ~ УСтУУе^Ус^СхУе.С + Уу^СхУеУ ) +

+УуУс (УСх^СхУР + У¥е^¥е;У,С )•             (^)

Слагаемое G^ определяет магнитную составляющую энергии Гиббса. Её определение следует

Gij =6^+—— + —-- Ук"КГ ^У; дуу к=Сху^еу ^Ук

где i и j - элементы замещения и внедрения соответственно. Парциальные величины реальных компонентов определятся следующим образом:

Gj = GiV; Gc = G,c - С,.у.

Карбидные фазы. В трехкомпонентной системе железо-хром-углерод возможно образование смешанных карбидов стехиометрического состава различного структурного типа. Замещающие металлические элементы (железо и хром) в этих карбидах образуют одну или более подрешеток, в которых все вакантные междоузлия (вакансии) заполняются углеродом. Так что подрешетка внедрения является комплектной, а концентрация элемента внедрения (углерода) равна единице (ус ⁼ 1)-

Энергии Гиббса карбидов с одной металлической подрешеткой (хромзамещенный цементит (Сг,Ге)3С, (Сг,Ге)7С3, Сг3С2) определятся выра жением

^т ~ УСх^СхУ ⁺ Тге^Ре.С ⁺ ^1^а(у_Ст 1п у_Сг +

⁺Ж ¹¹¹ Уре )] + ЖМг,Г=:С - (9) где а - стехиометрический коэффициент элементов металлической подрешетки.

Фаза	Параметр, Дж/моль	Примеч.
1	2	3
Жидкий расплав (Ж)	С“(ж) - отграфит) =!! 7369 _ 24,637 G^ - G^°yK) = 24335> 93 -11,427 + 2,37615 • 10"2177 G^1 -Я2°98 =-16459 + 335,618-7-5071п7 G^ - G^f' = 12040,17 - 6,558437 - 3,6751551 ■ 10"2177 С°р - ^298 = -10839,7 + 291,3027 - 467 In 7 Z°Y =-90526-25,9117 Z1^ = 80000 Z^r = 80000 £^ж' =-124320 + 28,57 Z^e = 19300 Z^ =49260-197 L°^e =-14550 + 6,657 ^CAFe =-516700 4$,Fe = 75500 Z^Fe = 47310	T<2180K 7>2180 T<1811 7>1811
О.ц.к. -твердый раствор (а, 5); а=15 с=3	G^ - Я2°98 = -8851,93 +157,487 - 26,90871n7 - - 0,0018943572 -1,47721 ■ 1О"673 +1392507"1 G*?^ - Я2°98 = -34864 + 344,187 - 5071n7 - 2,88526 • 1032 7"9 G^ -Я298 =+1224,83 + 124,1347-23,514371n7- -0,0043975272 - 5,89269 IO"873 + 77358,57"1 G^K) - Я298 = -25384,451 + 299,312557 - 467 In 7 +2,2960305 -IO317"9 G^K) -G^ -зс^^афит) = 416000 V-zF.K-z           VzF. V             V уоСоцк) _GO(OUK) _зсо(графит) = 322050 +75,667 7 1C.V        XV. V          V/                                 Z Z® = -1907 Y™Ky =-1907 ^cr+e-v =20500-9,687 ^cr+e-c = -1750000 + 9407 G^ =7?71п(р + 1)/(т) .    1 Г  .   79    158 ( 1   ,Y T4   T10    t16 Y тЛ|_    140/2  497^     2   45  200 J J 1 Гт"5 t"15 t"25 1 f ( т ) —------- Л|_ 10 315 1500 J , 518 Г 790 ( 1   ^1 1125[_ 497      J J p = 0,4	T<2180 7>2180 T<1811 7>1811 T<1 T>1

Окончание таблицы

1	2	3
	Тс = -311,5_Усг +1043yFe + уСг>>ре[1650 + 550(jCr - yFe)] Р = -0,008^Сг + 2,22^ре - 0,85yCr_yFe
_____ При отрицательных величинах Тс и Р, их значения следует поделить на -1
Г.ц.к. -твердый раствор (у); 0=1, с=\	G^ -G^0"^ = 7284 +0,163 Т G^ - G^ = -1462,4 + 8,2827 -1,157 In 7 + 6,4 ■ 10"4 72 G*™' - Я298 = -27098,266 + 300,252567 - 467 In 7 + 2,78854 • 10317"9 G°^ -G^ -б°(графит) = 25000 Gf^k) - С£№ - с^^афит) = 77207 -15,8777 L^.c = -26586-187 Z^v =-29686-187 ^=-34671 L^N =10833-7,4777 ®v = 14Ю
(Fe,Cr)3C	Gp^ - Я298 = -10745 + 706,047 -120,67 In 7 G°(M3C) -з^оС™») „^(графит) = -39744-18 087 Z^c =29260-16.637
(Fe,Cr)7C3	С^?Сз1 - Я298 = -209752 + 980,297 -170,57 In 7 - 0,069092172 GO(M7C3) _7(3о(оцк) _зсо(графит) = 113385-78,377 ZCr+e:C =-Ю465
(Fe,Cr)23C6	G^c6^-H^s =-521983 + 3622,247-620,9657 In 7-0,12643172 G^!6 1=20/ 23G“(r^3c6} + з / 23Gp^e23c6} Gp^23P6) = 20/23С“^2зСб) +3/23С°^33гСб) re.иг. u                 re.re.u               cr.ur.v Gp^S?61 - 23 / 3Gp^3C) + 5 / зс°(графит) = 66920 - 407 ге.ге.и              те.с             с Тс™ Fe с = -252350 + 80,47 сг,ге.сг,г с. с                        ’
Cr3C2	°сУсС2) -Я2°98 =-103719+ 496,83477-84,34967In7-0,032709572
Сигма-фаза (о)	Gv^crc, -22G°(°UK) -8GplruK) =92300-95,967 Л V.X-zI.VzI              V-/1                  А С GfeCrPe -4GiyuK)-8Gp<™K) + 18Gp•0',к, =117300-95,967 ГС.Сх.ГС                         JT V               JL V
С графит	Отграфит) _ Ho^ = -17369 +170,737 - 24,371n7 - 4,723 • 10"4 72 + + 25626007’1 - 2,643 • 108 7-2 +1,2 ■ 1010 7"3                    |

Для карбида состава (Cr,Fe)₂₃C₆ установлено наличие двух металлических подрешеток, в которых располагаются совместно атомы хрома и железа. Общей формулой такого карбида является (Cr,Fe)₂₀(Cr,Fe)₃C₆. Такое разделение металлов по двум подрешеткам (5 и t) позволяет представить энергию Гиббса такой системы уравнением

G_m⁼ У Ст УСт^Сг.Сг.С ⁺ УСгУре^СгТе:С ⁺

+УРеУСг^Ре:Сг:С + УРеУРе^РеТе^ +

+^ Л20(Ус_г In Усг + УРе !п Уре ) + ХУст ^b Усг ⁺ +Ур_е hl Ур_е )] + УсгУре (УСг^Сг,Ре:Сг:С ⁺Уре^€г,Ре:Ре:с) ^{+ +}УСгУре (УСг^Сг:Сг,Ре:С ⁺ Уре^Ре:Сг,Ре:С ) ⁺

⁺УСгУРеУСгУРе^Сг,Ре:Сг,Ре:С •                    (10)

В этой формуле G£r.Fe.c и GFe:Cr:C определяются через энергии Гиббса подрешеток, содержащих разноименные металлы

23Gcr:Fe:C “ 20^Cr:Cr:C + ^^Fe:Fe:C ’          ^ ^

23GFe:Cr;C = 20GFe;Fe;C + 3GCr:Cr:C.

Парциальные молярные энергии гипотетических «компонентов» можно рассчитать по формуле

G_ab.c =G_m Hl-Z^^Va-J^f ^-I Sy А )        V^b )

При использовании значении параметров модели (см. таблицу) будем иметь

^Cr:Fe:C ” ^Cr:Fe:C + ЖЖ (^Cr:Cr:C “ ^Cr:Fe:C “

~^Fe:Cr:C ⁺ ^Fe:Fe:C ) ⁺ 20 RT Ь y_Cr + 3RT Ь J_Fe +

"^УСтУре^УСт ⁺ У^е ”^ЖЖ)^Cr,Fe:Cr,Fe:C>

^Fe:Cr:C = ^Fe:Cr:C + ЖЖ (^Cr:Cr:C "^CrFe.C ~

^—^Fe:Cr:C + C:Fe:C ) + 20 RT b _Ж + 3^Thy_Cr +

+ЖЖ(Ж ⁺ Ж ”^УсхУ^^_Сх^_е^

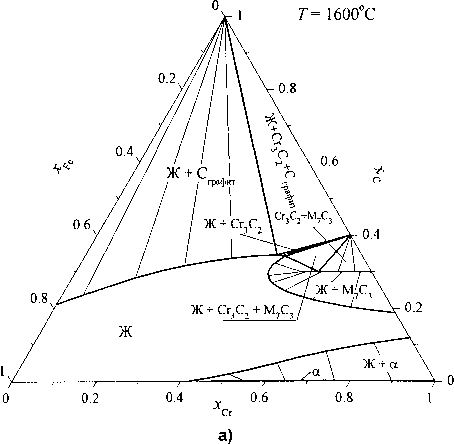
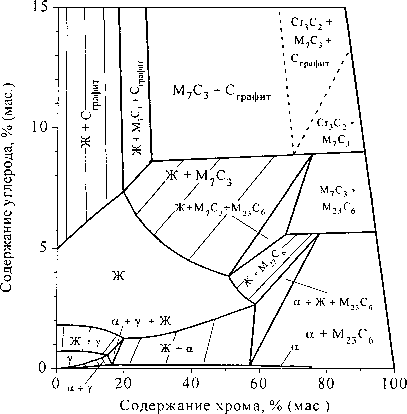
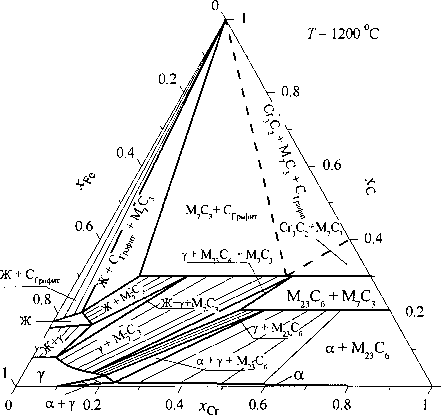
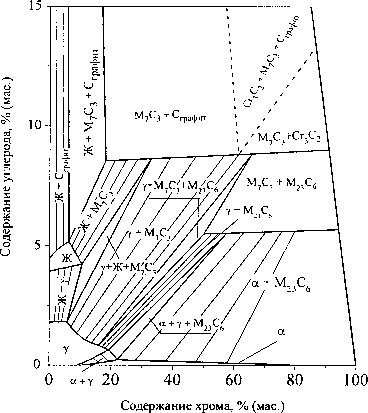
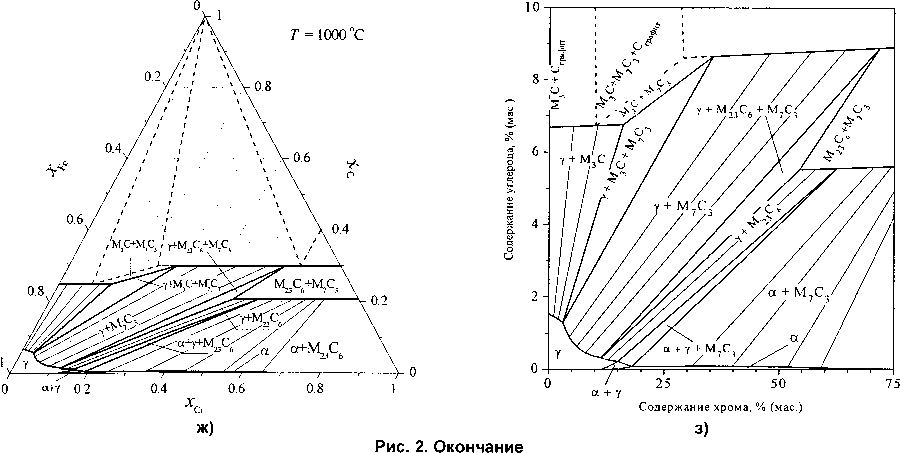
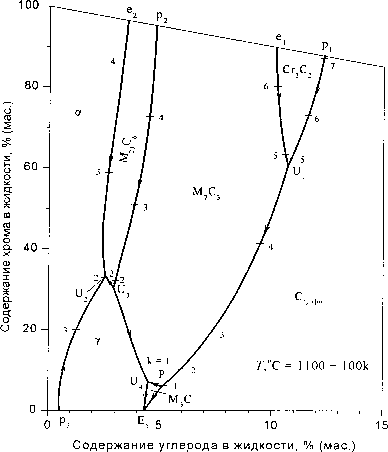
Графическая зависимость результатов расчета по полученным соотношениям представлена на рис. 2 в виде изотермических сечений и фазовых диаграмм металлического сплава в интервале температур 1600... 1000 °C. Из приведенных графических зависимостей следует, что при 1600 °C первично кристаллизующимся металлом является низкоуглеродистый феррит. Расплав, насыщенный углеродом, кристаллизуется с образованием карбида хрома Сг3С2 либо (Ге, Сг)7С3, что приводит к наличию двух трехфазных равновесий Ж + Сг3С2 +СграфИТ и Ж + М7С3 +Сг3С2. При уменьшении температуры до 1597 °C реализуется нонва-риантное равновесие

Ж + Сг₃С₂<=± М_ПС₃ + С^афщ..

Комплекс фаз, образующихся при кристаллизации жидкого расплава, графически представлен на рис. 3, б линиями трехфазного равновесия с участием

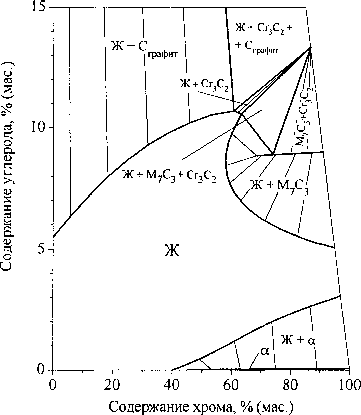
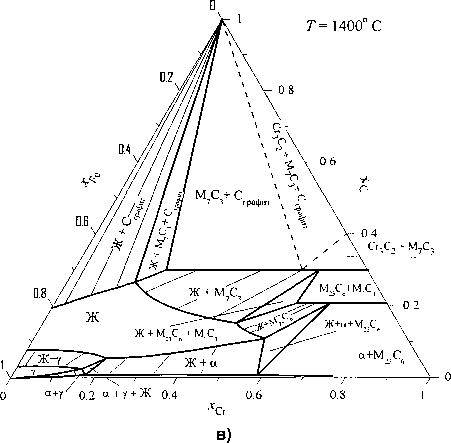
Рис. 2. Изотермические сечения и фазовые диаграммы металлического сплава системы железо-хром-углерод при температуре 1600(а, б), 1400 (в, г), 1200 (д, е), 1000 (ж, з)

а)

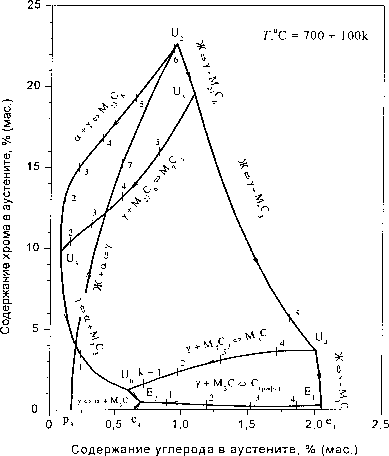
Рис. 3. Диаграммы трехфазных равновесий с участием аустенита (а) и жидкого сплава (б)

б)

О

С - Сг

С - Cr - Fe

С - Fe

Cr - Fe

1803 °C	Pi
Ж + Сгр	СгЗС2

1597

Ж + СгЗС2 о М7СЗ + Сгр

U1

1744	ei
ЖоСг7СЗ + СгЗС2

1577 Р2 Ж + Сг7СЗ <-> Сг23С6 е2

Ж <-» Сгр + Сг23С6

Cr3C2 + M7C3 + Сгр

Ж + М7СЗ + Сгр

а + у + М23С6

Ж + у + М7СЗ

" у + М7СЗ + МЗС

у + М23С6 + М7СЗ

у + а + М7СЗ

Ж + а<-»у+М23С6

Ж + М23С6оу+М7СЗ

Ж + М7СЗ + МЗС

Ж+М7СЗоу + МЗС

Ж + у + МЗС

у+М23С6оа + М7СЗ

и2

Ж + у + М23С6

Ж + М7СЗ + Сгр о МЗС

Ж + МЗС + Сгр

Жоу + МЗС + Сгр

и5

а + М23С6 + М7СЗ

у + МЗСоа + М7СЗ

и6

а + ст + М23С6

МЗС + М7СЗ + а

у + а + МЗС

у + МЗС + Сгр

у <-> а + МЗС + Сгр

1495	е2
Ж + 6<-		у

1154	Сз
Ж = у	+ Сгр

Вестник ЮУрГУ, № 36, 2009

а + МЗС + Сгр

658

МЗС о а + М7СЗ + Сгр

Е3 '

а + М7СЗ + Сгр

570 М7СЗ + Сгроа + СгЗС2 и7 а + СгЗС2 + Сгр а + М7СЗ + СгЗС2

МЗС + М7СЗ + Сгр

а(Сг)+ ст + М23С6

а(Ре) + ст + М23С6

512

аГСг) + a(Fe) + ст + М23С6

D

а(Сг) + а(Ре) + ст + М23С6

Рис. 4. Схема фазовых превращений в системе железо-хром-углерод

е5

ст <-» а(Сг) + а(Ре)

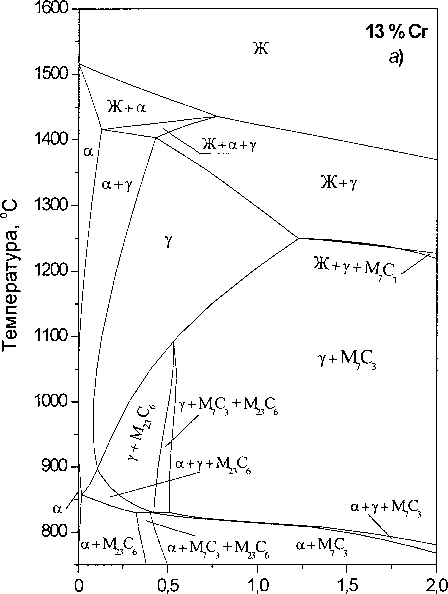
Содержание углерода, % (мае.)

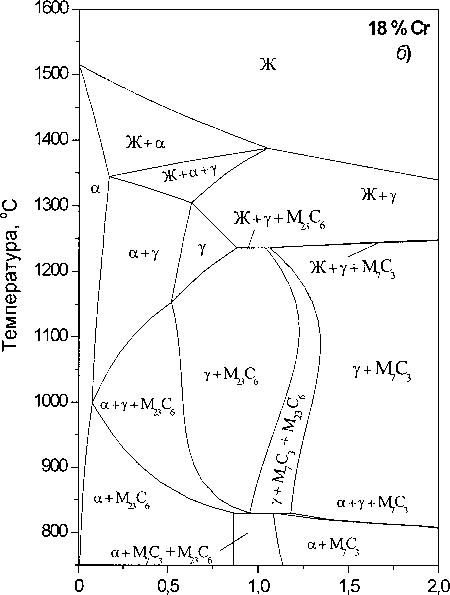
Содержание углерода, % (мае.)

Рис. 5. Политермические разрезы диаграммы состояния системы Fe-Cr-C при содержании хрома в металле 13%(а) и 18 % (6)

жидкости. Области между кривыми определяются как политермические поверхности растворимости компонентов в расплаве, равновесном с одной из кристаллизующихся фаз.

При температуре 1400 °C (рис. 2, в, г) и небольших концентрациях хрома первично кристаллизующимся металлом будет аустенит. Возможно также образование карбида М2зС6 в равновесии с жидким расплавом или ферритом. Дальнейшее снижение температуры приводит к расширению концентрационных пределов устойчивости аустенита и трансформации, равновесных с металлом, карбидов. Фазовые превращения с участием аустенита графически представлены на рис. 3, а. Координаты точек пересечения кривых определяют температуры и концентрации компонентов нонва-риантных превращений с участием г.ц.к.-фазы (аустенита).

Совокупность фазовых превращений в сопоставлении с реакциями в бинарных системах представлена на рис. 4.

На изотермических сечениях при заданной концентрации одного из компонентов можно установить последовательность фазовых превращений и определить количественные соотношения равновесных фаз. Однако наиболее представительными и удобными для анализа являются политермические разрезы при постоянной концентрации одного из компонентов. На рис. 5 приведены такие политермические сечения, соответствующие содер жанию хрома в металлическом сплаве 13 и 18% (по массе) и различной концентрации углерода.

Выводы. Проведен термодинамический анализ и изучены фазовые равновесия в трехкомпонентной системе железо-хром-углерод. Рассчитаны и построены изотермические сечения в интервале температур 1600... 1000 °C. Приведена графическая зависимость проекции поверхности ликвидуса и диаграмма трехфазных равновесий с участием аустенита. Результаты расчета представлены также в виде политермических разрезов с постоянным содержанием хрома в металле.

Работа выполнена в соответствии с научной программой Федерального агентства по образованию - «Развитие научного потенциала высшей школы (2009-2010 гг.)», код проекта - 713 и при поддержке РФФИ, грант № 08-08-00416.