Термодинамический анализ системы H2 - O2 - C

Автор: Кузнецов Юрий Серафимович, Качурина Ольга Ивановна, Малютина Елена Михайловна, Вяткин Герман Платонович, Гольдштейн Владимир Яковлевич, Дукмасов Владимир Георгиевич, Чаплыгин Борис Александрович, Пластинин Борис Глебович

Журнал: Вестник Южно-Уральского государственного университета. Серия: Металлургия @vestnik-susu-metallurgy

Рубрика: Физическая химия и физика металлургических систем

Статья в выпуске: 4 т.18, 2018 года.

Бесплатный доступ

В гетерогенной смеси «Н2 - О2 - С» при повышенных температурах в результате протекания реакций окисления, ре акции водяного газа и двух реакций газификации углерода об разуется газовая смесь (H2 - H2O - CO - CO2). В работе выполнен термодинамический анализ возможных процессов, протекающих при температурах 700-1500 К в системе «Н2 - О2 - С». Определены равновесные параметры получающихся газовых композиций - их состав и окислительно-восстановительнные свойства. В любой газовой смеси, содержащей H2O и (или) CO2, весьма низкую концентрацию кислорода, образующегося в результате диссоциации H2O и CO2, принято определять величиной атм). При заданном общем давлении эта величина рассчитывается по составу газовой смеси и справочной информации по реакциям диссоциации H2O или CO2. Результаты выполненного анализа представляются двумя номограммами. Такие номограммы, во-первых, являются наглядным, альтернативным табличному, способом представления весьма обширной информации по свойствам сложных газовых атмосфер. Во-вторых, с использованием номограмм и справочной информации по упругостям диссоциации оксидов металлов можно оценить параметры восстановления этих оксидов. В бинарных газовых смесях (CO - CO2) и в водяном газе (H2 - H2O - CO - CO2) при определенных сочетаниях состава и температуры возможно образование сажистого углерода. Этим объясняется существование ограничений при температурах ниже ~ 1100 К в получении водяного газа с любыми концентрациями компонентов. Возможны различные по технологической и экономической целесообразности способы получения газовых смесей. В частности, при нагревании паров воды в контакте с избытком углерода до ~ 1100 К получается практически чистая эквимолярная смесь (H2 - CO) с высоким восстановительным потенциалом. Введение в эту систему водорода позволяет получить газовые смеси с чрезвычайно низким давлением кислорода, и это делает термодинамически возможным восстановление оксида любого металла. Проанализирована целесообразность представления полученной информации трехмерной диаграммой, построенной на концентрационном треугольнике «Н2 - О2 - С». Учет реакций образования метана приводит к заметным изменениям равновесных параметров газовых смесей лишь при температурах ниже примерно 900 К.

Еще

Водород, кислород, углерод, оксиды водорода и углерода, водяной газ, диссоциация паров воды и диоксида углерода, кислородный потенциал, сажистый углерод, hydrogen аnd carbon oxides

Короткий адрес: https://sciup.org/147232516

IDR: 147232516 | DOI: 10.14529/met180401

Текст научной статьи Термодинамический анализ системы H2 - O2 - C

Важнейшие металлургические процессы восстановления металлов практически всегда осуществляются с использованием твердого углерода и газовых фаз, основой которых является водяной газ H2 – H2O – CO – CO2. В реальных технологиях, например [1–8], создаются оптимальные параметры процессов восстановления металлов: избыток углерода (кокса), температура, состав газовой смеси. Любой процесс получения металлов из окси- дов связан с приготовлением восстановительной газовой смеси [9–13]. Выбор способа приготовления смеси должен базироваться на результатах термодинамического анализа системы H2 – O2 – C при повышенных температурах [9]. Результаты анализа вместо многочисленных громоздких таблиц можно представить различными номограммами [14] либо пространственной диаграммой, построенной на концентрационном треугольнике H2 –O2 – C [9].

Точки области I на концентрационном треугольнике (рис. 1) определяют возможные концентрации компонентов смеси H2O – CO2 – O2. Штриховые линии 1, 2 и 3 определяют газовые смеси, концентрации кислорода в которых равны 75, 50 и 25 мол. %. Область II определяет возможные параметры состояния водяного газа. Квазибинарное сечение nk, определяющее концентрацию смеси H2O – CO2, следует при повышенных температурах считать условной линией, разделяющей области I и II. На самом деле в смеси H2O – CO2 из-за диссоциации H2O и CO2 присутствуют незначительные количества O2, H2, CO и тем большие, чем выше температура. Штриховая линия 4, положение которой зависит от температуры, определяет состав водяного газа со следами H2, CO и O2.

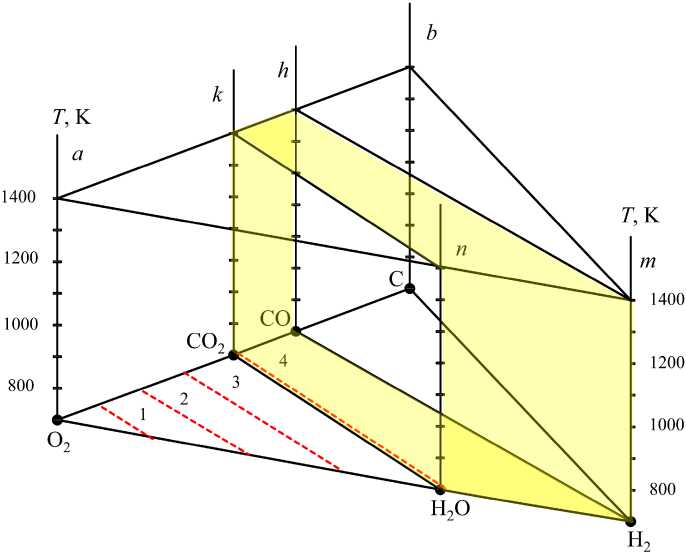
Рис. 1 а . Пространственная диаграмма системы C – O 2 – H 2 для интервала температур 700–1400 К

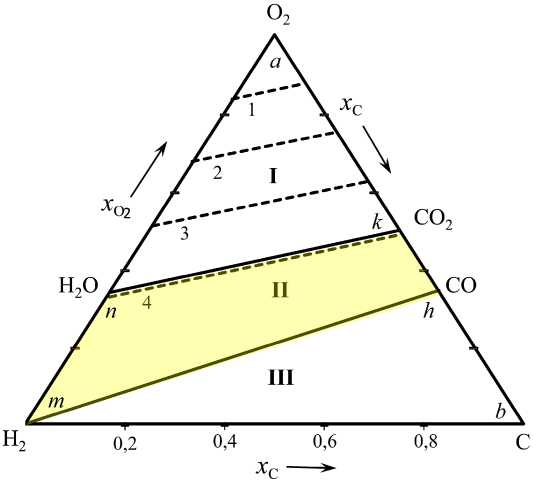
Рис. 1 б . Концентрационный треугольник системы H 2 – O 2 – C

Нижняя граница области II тоже не совпадает с линией квазибинарного сечения mh. Положение этой границы зависит от температуры и при температурах ниже 1100 К несовпадение границы с линией mh весьма существенно. Для определения положения этой граничной линии следует рассчитать возможные параметры равновесия водяного газа с углеродом Н2 – Н2О – СО – СО2 – С. Эти параметры должны определяться совместными равно- весиями реакции водяного газа и двух реакций газификаций углерода (стандартное изменение энергии Гиббса здесь и далее определяется в Дж):

В соответствии с правилом фаз Гиббса такая трехкомпонентная двухфазная система при фиксированном давлении и заданной температуре имеет одну степень свободы с = к – ф = 3 – 2 = 1.

Следовательно, для решения системы трех уравнений необходимо задавать какой-либо параметр равновесной системы. Если задать концентрацию СО, получаем такие уравнения для расчетов xCO , xH O и xH при заданной концентрации xCO и P = 1 атм:

x CO₂

x C ² O ;

^K 2 ^;

H2 +CO2=H2O+CO,

A r G T (1) = 36 580 - 33,465 ■ T ;

¹ x CO x CO₂ x H 2 O = ----ТЛ---

C+CO = 2CO,

² (2)

A r G T (2) = 172140 - 177,7 ■ T ;

C+H O=CO+H ,

2 2 (3)

A G ^ (3) = 135 560 - 144,235 ■ T .

Из этих трех реакций лишь две независимые – любая из них может быть получена комбинацией двух других. Если рассматривать совместные равновесия, например, двух независимых реакций (1) и (2), то получаем систему трех расчетных уравнений с четырьмя неизвестными:

K 1

p H ₂ O ■ p CO p H ₂ ■ p CO ₂

x . x A G (1)

x H₂O x CO

—²------ = e ^RT ; (4)

x h₂ ■ x CO ₂

2 2 _ ^A r G T (2)

K2 _ A» _ xCO ■ p = e RT ;(5)

pCO2

^ xi _ xCO + xH2O + xCO2 + x H2 = 1.

x _ ¹ x CO ⁽ x CO / K 2 ) _;

^H 2 1 + ( x CO / K 3 ) ;

xH2 _ 1 ■ xco _ a xH2O K1 xCO2

В соответствии с методом комбинирования реакция (3) получается вычитанием уравнения реакции (1) из уравнения реакции (2), то есть отношение констант K ₂/ K ₁ равно константе равновесия K ₃.

Для примера в табл. 1–3 приведены ре- зультаты расчетов возможных составов равновесного с углеродом водяного газа для трех температур 800, 1000 и 1500 К, а на рис. 2 штриховыми линиями приведены нижние границы области II для шести температур в интервале 700–1500 К. Эти штриховые линии являются проекциями на концентрационный треугольник следов пересечения изотермиче-

Таблица 1

Параметры равновесия систем «Н 2 – Н 2 О – СО – СО 2 – С», вычисленные при заданных концентрациях СО, Т = 800 К, 1 атм

x CO	x CO₂	x H₂O	x H 2	(x x H O lg x, V ^H2 7	1g [ x C⁰^ 1 V ^x co 7	lg( p _O ₂ , атм )
0	0	0	1	–	–	– ∞
0,01	9,07Л0 ^-3	0,199	0,9610	–1,6839	–0,0424	–27,85
0,02	3,63 ■Ю ^-2	0,2768	0,6069	–0,3819	0,2584	–27,25
0,03	8,16 ^ 10 ^-2	0,3409	0,5475	–0,22058	0,4346	–26,89
0,05	0,2267	0,3684	0,3549	0,0162	0,6564	–26,45
0,0571	0,2959	0,3511	0,2959	0,0743	0,7145	–26,33
0,07	0,4442	0,2877	0,1981	0,1621	0,8025	–26,16
0,08	0,5802	0,2121	0,1277	0,2203	0,8605	–26,04
0,09	0,7344	0,1143	0,0612	0,2716	0,9117	–25,94
0,0920	0,7678	0,0920	0,0482	0,28907	0,9215	–25,92
0,0996	0,9004	0	0	–	0,9560	–25,85

Таблица 2

x CO	x CO₂	x H₂O	^x H₂	x _{H O} lg x„ к ^H2 J	1 1 ^x CO₂ 1 ^lg l1 к ^x CO J	^lg( p O₂ , атм )
0	0	0	1	–	–	- то *
0,001	5,12 - 10 ^-7	3,7 - 10 ^-3	0,9953	–2,426	–3,290	–26,96
0,03	4,61 - 10 ^-4	0,0112	0,9588	–1,9325	–1,813	–23,95
0,05	1,28 - 10 ^-3	0,0164	0,932	–1,7540	–1,5907	–23,56
0,10	5,12 - 10 ^-3	0,0305	0,864	–1,4529	–1,2905	–22,96
0,20	0,0205	0,0513	0,728	–1,1520	–0,9892	–22,36*
0,30	0,0461	0,0625	0,591	–0,9757	–0,8134	–22,01
0,40	0,0819	0,0639	0,454	–0,8516	–0,6888	–21,76*
0,50	0,1281	0,0557	0,316	–0,7538	–0,5914	–21,56
0,60	0,1844	0,0376	0,178	–0,6752	–0,5133	–21,41*
0,70	0,251	0,0097	0,0393	–0,6076	–0,4454	–21,27
0,7283	0,2717	0	0	–	–0,4325	–21,24*

* Информация приведена на рис. 5 линиями 5-9.

Таблица 3

^x CO	^x CO₂	^x H₂O	^x H₂	x H O ^lg x„ к ^H2 J	1 1 ^x CO₂ 1 ^lg l1 к ^x CO J	^lg( p O₂ , атм )
0	0	0	1	–	–	- » *
0,05	1,3-Ю ^-6	7,3 - 10 ^-5	0,95	–4,1144	–4,5865	–19,71
0,10	5,1-Ю ^-6	1,4-Ю ^-4	0,90	–3,8081	–4,2915	–19,12*
0,20	2,0 - 10 ^-5	2,5-Ю ^-4	0,80	–3,5051	–4,0015	–18,54
0,30	4,6 - 10 ^-5	3,2-Ю ^-4	0,70	–3,3399	–3,8165	–18,17*
0,40	8,2 - 10 ^-5	3,7-Ю ^-4	0,60	–3,2099	–3,6865	–17,91
0,50	1,3-Ю ^-4	3,8-Ю ^-4	0,50	–3,1192	–3,5864	–17,71*
0,60	1,9-Ю ^-4	3,7 -Ю^-4	0,40	–3,0339	–3,5015	–17,54
0,70	2,5-Ю ^-4	3,2-Ю ^-4	0,30	–2,9720	–3,4465	–17,43*
0,80	3,3-Ю ^-4	2,5-Ю ^-4	0,20	–2,9031	–3,3865	–17,31
0,90	4,1 - 10 ^-4	1,4-Ю ^-4	0,10	–2,8539	–3,3415	–17,22*
0,9995	5 ⋅ 10^–4	0	0	–	–	–17,14*

* Информация приведена на рис. 2 линиями 1-7.

Параметры равновесия систем «Н 2 – Н 2 О – СО – СО 2 – С», вычисленные при заданных концентрациях СО, T = 1000 К, 1 атм

Параметры равновесия системы «Н 2 – Н 2 О – СО – СО 2 – С», вычисленные при заданных концентрациях СО, T =1500 К, 1 атм

скими плоскостями криволинейной поли-термической поверхности (рис. 3), определяющей состав водяного газа в равновесии с углеродом. Слева все изотермы сходятся в точке m, первые строки табл. 1–3. Справа изотермы пересекают линию hk в точках, координаты которых определяют концентрацию смеси CO2 – CO, равновесной с углеродом, последние строки табл. 1–3. Каждая из множества точек на таких изотермах определяет возможный состав водяного газа, равновесного с углеродом. При температуре 1500 К в водяном газе, равновесном с углеродом, концентрации H2O и CO2 практически равны нулю и нижняя граница области II совпадает с квазибинарным сечением mh. Штриховые линии, соединяющие точки граничных линий с точкой b, являются конодами, соответствующими строго определенным величинам кислородных потенциалов газов (расчет приведен ниже). Концы конод определяют природу и состав равновесных фаз. На рис. 2 показаны коноды для температуры 1500 К (табл. 3), на рис. 4 – для 800 К (табл. 1) и на рис. 5 – для 1000 К (табл. 2).

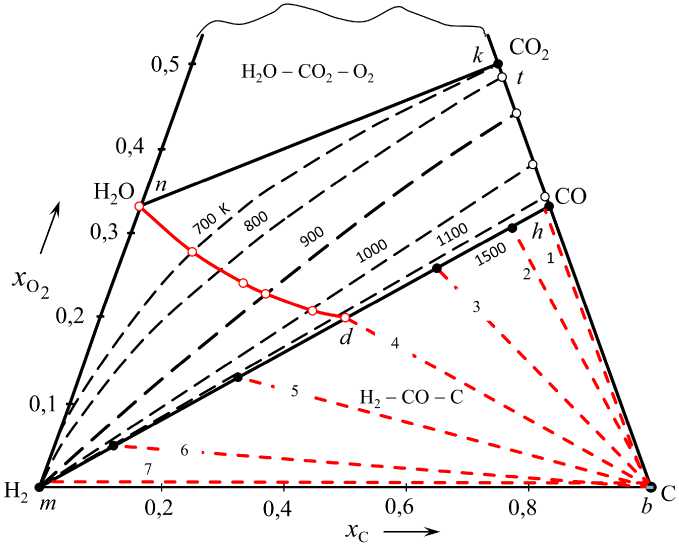
Рис. 2. Изотермы параметров водяного газа, равновесного с углеродом: изотермы 700–1500 К определяют нижние границы области II; линии 1–7 определяют кислородный потенциал водяного газа, равновесного с углеродом при 1500 К, lg( p_O^, атм) = -17,14 (1), –17,22 (2), –17,49 (3), –17,71 (4), –18,17 (5), –19,12 (6) и – ∞ (7), табл. 3; линия nd – параметры водяного газа, получающегося при нагревании паров воды в контакте с избытком углерода, табл. 8

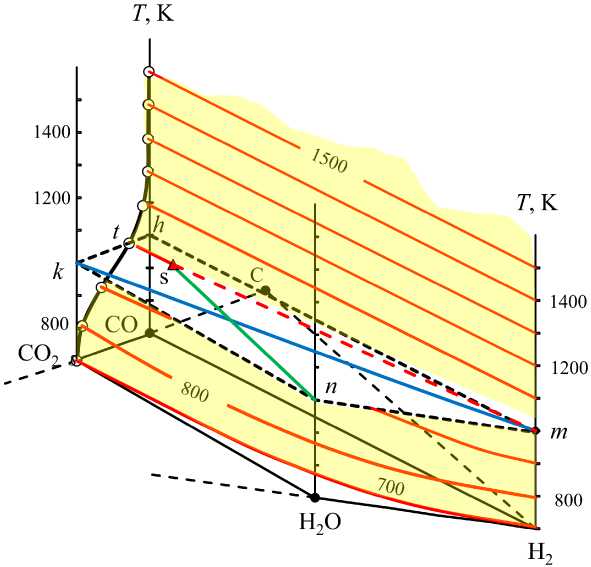
Рис. 3. Поверхность параметров системы (Н 2 – Н 2 О – СО – СО 2 – С): tmnkt – область возможных cоставов водяного газа в отсутствии углерода при 1000 К, линия km – cоставы водяного газа, получающегося из (Н 2 – СО 2 ), линия ns – cоставы водяного газа, получающегося из (Н 2 О – СО)

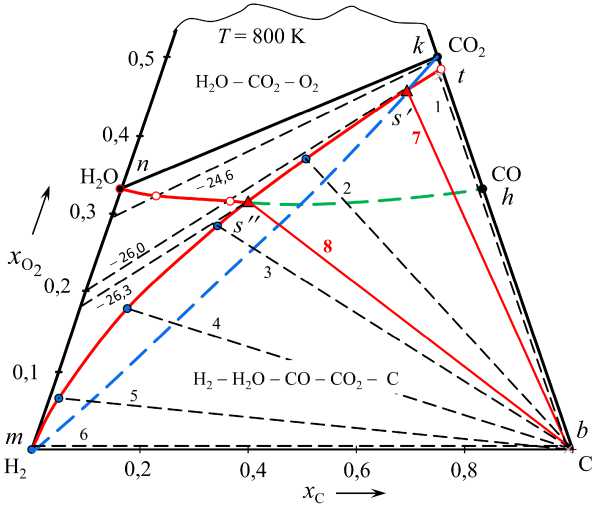
Рис. 4. Примеры возможных параметров водяного газа при 800 К: линия ks ′ – газ получается нагреванием исходных смесей (Н 2 – СО 2 ) состава a _o / d _o = 0,14 / 0,86 (точка s ′ ), 1/9, СО 2 ; линия ns ′′ – газ получается нагреванием исходных смесей (СО – Н 2 О), c _o / b _o = 0 , 353 / 0,647 (точка s ′′ ), 3/7, 1/9, Н 2 О; коноды 1–6 определяют кислородный потенциал водяного газа, равновесного с углеродом, lg( p _O , атм) = –25,85 (1), –26,04 (2), –26,89 (3), –27,25 (4), –27,85 (5) и – ∞ (6); конода 7 определяет кислородный потенциал водяного газа, получающегося из смеси (Н 2 – СО 2 ) и равновесного с углеродом, lg( p _O , атм) = –25,92 ; конода 8 определяет кислородный потенциал водяного газа, получающегося из смеси (Н 2 О – СО) и равновесного с углеродом, lg( p _O , атм) = –26,33

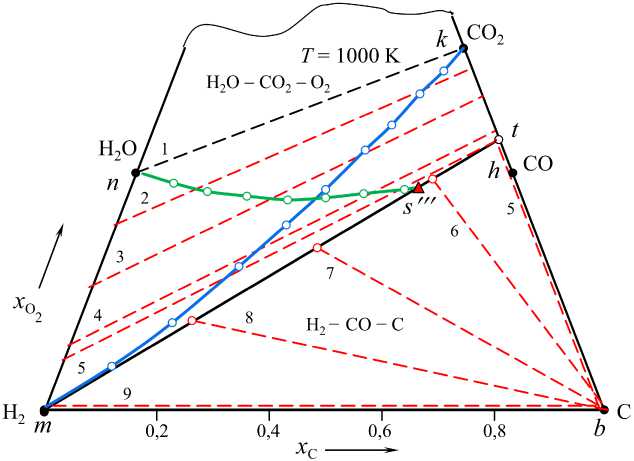
Рис. 5. Параметры водяного газа при 1000 К: линия mt – граница областей II и III определяет возможные параметры систем «H 2 – H 2 O – CO – CO 2 – C»; линии 1–5 определяют возможные составы и кислородный потенциал газа, lg( p _O , атм) = –6,7 (1), –19 (2), –20 (3), –21 (4) и –21,24 (5); линии 6–9 определяют кислородный потенциал водяного газа, равновесного с углеродом –21,41 (6), –21,76 (7), –22,369 (8) и – ∞ (9); линия mk – газ получается нагреванием исходных смесей (Н 2 – СО 2 ); линии ns ′′′ t – газ получается нагреванием смесей (Н 2 О – СО)

Возможно множество способов получения водяного газа нагреванием какой-либо исходной системы. Каждый из них позволяет получить газ строго определенного состава, но нет единого способа, позволяющего получить водяной газ любого равновесного состава. Проиллюстрируем это несколькими примерами.

Пример 1 – получение водяного газа нагреванием до 800 и 1000 К смесей H 2 – CO 2 разного состава. Стандартная процедура расчета состоит в следующем:

	Н 2	+ СО 2	= Н 2 О	+ СО
Исходный состав	a o	d o	–	–
Равновесный состав	( a o – x ) ( d o – x )		x	x

Здесь ao и do – числа молей Н2 и СО2 в исходной смеси, x – количества продуктов. При расчетах положим (ao + do) = 1 моль, тогда величины a = (ao – x), d = (do – x), b = x и c = x будут определять и количества и молярные доли компонентов равновесного водяного газа. Получаем для равновесия реакции (1)

K 1 =

( a o - x ⁾⁽ d o - x )

Решение этого квадратного уравнения (при K i ^ 1) таково:

x CO = x Н 2 О

0,5 • K i ± K i • a o • d o + 0,5 • K i f 1 - K i N 1 — K i I 1 — K i J

x h₂ = ⁽ a o ^- x );

x CO 2 = ⁽ d o ^- x ^).

Физический смысл имеет один из двух корней решения квадратного уравнения, причем для Ki < 1 перед квадратным корнем следует ставить знак «+», а для Ki > 1 - знак «-». При K1 = 1 (1093 К) из уравнения (8) получаем x = aoldo. (9*) ao + do

Результаты расчетов, табл. 4 и 5, линии mk на рис. 4 и 5 следует скорректировать из-за протекания реакции диссоциации

2CO = CO 2 + C.

В водяном газе, получающемся при нагревании до 800 К смесей состава a o / d o ≤ 0,14 / 0,86 (выделено жирным курсивом в табл. 4), реализуются состояния, определяемые фрагментом ks ′ линии mk на рис. 4. При нагревании смесей с a o / d o > 0,14 / 0,86 происходит выделение сажистого углерода и реализуются состояния, определяемые линией s ′ m (табл. 1). При нагревании до 1000 К смесей Н 2 – СО 2 любого состава выделение сажистого углерода не происходит, линия mk на рис. 5.

Таблица 4

Возможные ( курсив ) параметры равновесия водяного газа, получающегося при нагревании смесей (Н 2 , a _o моль + СО 2 , d _o моль) до 800 К

a _o d _o	0,8 0,2	0,6 0,4	0,4 0,6	0,2 0,8	0,14/0,86	0,1/0,9
x _СО = x _H ₂ _O	0,1153	0,1570	0,1570	0,1153	0,0920	0,0724
x H 2	0,6848	0,4430	0,2430	0,0848	0,0482	0,0276
x CO₂	0,0848	0,2430	0,4430	0,6848	0,7678	0,8276
lg( p _O ₂ , атм)	Состояния не реализуются				–25,92	–25,64

Таблица 5

Параметры равновесия водяного газа, получающегося при нагревании смесей (Н 2 , a o моль + СО 2 , d o моль) до1000 К

a o d _o	0,9 0,1	0,8 0,2	0,6 0,4	0,4 0,6	0,2 0,8	0,1 0,9
x СО = x _H ₂ _O	0,0866	0,1498	0,2183	0,2183	0,1498	0,0866
x H₂	0,8134	0,6502	0,3817	0,1817	0,0502	0,0134
x CO₂	0,0134	0,0502	0,1817	0,3817	0,6502	0,8134
lg( p _O ₂ , атм)	–22,00	–21,33	–20,54	–19,89	–19,10	–18,44

Таблица 6

Возможные (курсив) параметры равновесия водяного газа, получающегося при нагревании смесей (Н2О, bo моль - СО, co моль) до 800 К

с o b _o	0,8 0,2	0,6 0,4	0,4 0,6	0,353/0,647	0,3/0,7	0,2/0,8	0,1/0,9
x _H ₂ = x _CO ₂	0,1870	0,3179	0,3179	0,2959	0,2636	0,1870	0,0973
x СО	0,6130	0,2820	0,0820	0,0571	0,0364	0,0131	0,0027
x H₂O	0,0130	0,0820	0,2820	0,3511	0,4364	0,6130	0,8027
x H₂ / x H₂O	14,328	3,8760	1,127	0,8428	0,604	0,35	0,1212
x СО / x _CO ₂	3,279	0,887	0,258	0,1930	0,1382	0,0698	0,0277
lg( p _O ₂ , атм)	Состояния не реализуются			–26,33	–26,04	–25,45	–24,65

Таблица 7

Параметры водяного газа, образующегося при нагревании до 1000 К смесей (Н2О, bo - СО, co моль)

с _o b _o	0,9 0,1	0,777/0,223	0,7/0,3	0,5/0,5	0,3/0,7	0,1/0,9
x H₂ = x CO₂	0,0866	0,1837	0,1931	0,2267	0,1931	0,0866
x СО	0,8134	0,5933	0,5069	0,2733	0,1069	0,0134
x H₂O	0,0134	0,0393	0,1069	0,2733	0,5069	0,8134

Пример 2 – получение водяного газа нагреванием смесей H 2 O – CO разного состава. Рассчитывается равновесие реакции

Н 2 О + СО = Н 2 + СО 2 (1*) с константой К ^; = 1/ К 1 по уравнениям, аналогичным уравнениям (9):

^x CO₂ = ^х н₂

0,5 • К

1 - К

K ' b +( " K 1 ;

1 - к ; ( 1 - к ; )

^x H₂O = b o ^x H₂ ^;
^Х СО = ^co ^x CO₂ .

Результаты расчетов по этим уравнениям, табл. 6 и 7, линии nh на рис. 4 и 5 тоже следует скорректировать из-за протекания реакции диссоциации

2CO = CO 2 + C.

В газе, получающемся при 800 К из смесей состава c _o/ b _o < 0,353/0,647 (выделено жирным курсивом в табл. 6), реализуются состояния, определяемые фрагментом ns ′′ линии nh на рис. 4. Состояния s ′′ h в равновесии не возможны – выделяется сажистый углерод и реализуются состояния, определяемые линией s ′′ t . При нагревании до 1000 К смесей Н 2 О – CО состава c _o/ b _o < 0,777/0,223 , табл. 7, реализуются состояния, определяемые линией ns ′′′ , рис. 5.

Пример 3 – получение водяного газа нагреванием паров воды в контакте с углеродом. Этот способ представляет наибольший практический интерес из-за простоты и незначительных затрат.

Образование водяного газа при нагревании паров воды в контакте с углеродом является следствием протекания трех реакций: в результате реакции (3) образуются H 2 и CO, диоксид CO 2 образуется по реакциям

CO + H 2 O = CO 2 + H 2 ;

2CO = CO 2 + C.

Углерод расходуется по реакции (3) и образуется сажистый углерод при диссоциации CO, реакция (2*) . Можно определить вклад каждой из реакций (3) и (2*) в расход и обра-

зование углерода системы:

при нагревании

исходной

Исходное состояние Равновесие Равновесие

CO 2

–

= 2CO;

–

( y – 2 s )

Исходное состояние Равновесие Равновесие

+ H 2 O

b о b ( b о – y )

= CO

–

( y – 2 s )

+ H 2

–

a y

Здесь в первой строке после уравнений реакций показано количество паров воды в исходном состоянии b _о моль. Во второй строке –

x H 2

S ^; x H₂O =

S ; x co =

S ; x CO 2

количества газов в системе после изотермической выдержки паров воды в контакте с углеродом. В третьей строке – то же самое с учетом вклада каждой из реакций газификации в образовании равновесной газовой фазы:

y – количество углерода (моль), вступившего в реакцию (3), s – количество углерода (моль), образовавшегося по реакции (2*).

Тогда константы равновесия реакций и

После замены в этих уравнениях a , b , c , d и ∑ на величины y , ( b о – y ), ( y – 2 s ), s и ( b о + y – s ) получаем и такие расчетные формулы:

5 = 2

—

y ²

4 K ^;

- (b o (b o ^— У) ⁺ ² У K ₂

условие нормировки представляются такими

уравнениями:

K 3 =

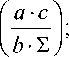
Г c 2 )

d-SJ

S = a + b + c + d.

Решение этой системы трех уравнений с четырьмя неизвестными с учетом баланса по водороду и кислороду:

b o = a + b , b o = b + c + 2 d

представляется уравнениями:

a2 , , , a - c c=—K----------; b = bo—a; d=-^;

² 3 ( b o ^— ^a ) + ^a

K ₂

a = у ; b = b o — у ; d = 5 ; c = у — 2 5 ;

S = a + b + c + d = bo + у — 5.

Из результатов расчетов (табл. 8) следует:

– при нагревании паров воды в контакте с избытком углерода получается водяной газ строго определенного состава в зависимости от температуры;

– получается газовая смесь, состав которой определяется точками пересечения линии nd c изотермами, рис. 2 и 6;

– при нагревании до температур выше примерно 1200 К получается практически чистая эквимолярная смесь CO – Н 2 (точка d , рис. 2) с высоким восстановительным потенциалом.

Из приведенных примеров следует, что нет единого способа получения водяного газа всех возможных составов, которые определяются бесконечным множеством точек в области II концентрационного треугольника,

Таблица 8

Параметры равновесия систем «Н 2 – Н 2 О – СО – СО 2 – С», получающихся при нагревании исходной системы «Н 2 О (1моль) – С», давление 1 атм, линия nd на рис. 2

T , К	700	850	900	1000	1100	1300	1500
y = n C (15)	0,3059	0,6265	0,7265	0,8860	0,9640	0,9960	0,9993
s = n C (2)	0,1495	0,2476	0,2328	0,1207	0,0327	0,0021	0,00023
∑ n C = y – s	0,1564	0,3789	0,4937	0,7653	0,9313	0,9939	0,9990
a , моль	0,3059	0,6265	0,7265	0,8860	0,9640	0,9960	0,9993
b , моль	0,6941	0,3735	0,2735	0,1140	0,0360	0,0040	0,0007
c , моль	0,0069	0,1313	0,2608	0,6447	0,8986	0,9918	0,9988
d , моль	0,1495	0,2476	0,2328	0,1207	0,0327	0,0021	0,00023
∑, моль	1,1564	1,1389	1,4937	1,7653	1,9313	1,9939	1,9991
V , л	66,38	96,11	110,23	144,8	174,2	212,6	245,9
x H 2	0,2645	0,4543	0,4864	0,5019	0,4991	0,4994	0,4999
x H₂O	0,6003	0,2709	0,1831	0,0646	0,0186	0,0021	0,0004
x CO	0,0059	0,0953	0,1746	0,3652	0,4653	0,4974	0,4996
x CO₂	0,1293	0,1795	0,1559	0,0683	0,0170	0,0011	0,0001
x H₂O / x H₂	2,2696	0,5963	0,3764	0,1287	0,0373	0,0042	0,0008
lg( x _H ₂ _O / x _H ₂ )	0,356	–0,225	–0,424	–0,890	–1,429	–2,376	~ –3,1
x CO₂ / x CO	21,92	1,8835	0,8929	0,1870	0,0365	0,0022	0,0002
lg( x _CO ₂ / x _CO)	1,341	0,275	–0,049	–0,728	–1,437	–2,655	~ –3,7
(lg p _O ₂ )	–30,36	–25,04	–23,76	–21,84	–20,57	–18,89	–17,68

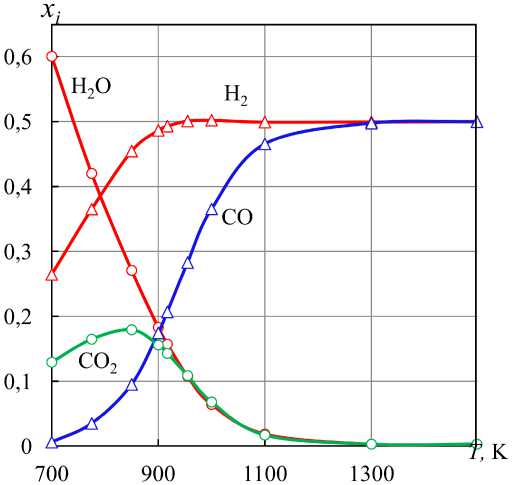
Рис. 6. Концентрации компонентов водяного газа, получающегося при нагревании паров воды в контакте с углеродом

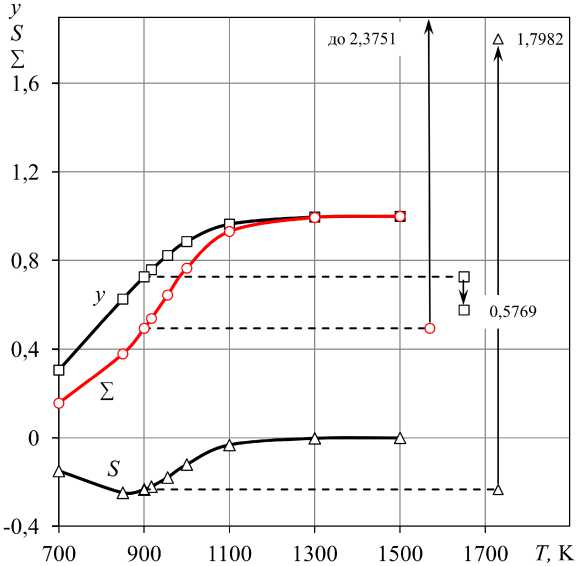
Рис. 7. Количества газифицированного углерода при нагревании исходной системы «Н 2 О (1 моль) – С»: y и ∑ n C – газификация углерода, s – сажистый углерод; стрелки – сравнение количеств газифицированного углерода при 900 К систем «Н 2 О (1) – С» и «Н 2 О (1) – СО 2 (9 моль) – С», табл. 2.26

рис. 1. Нагреванием, например, до 800 К смесей (H 2 – CO 2 ) и (H 2 O – CO) можно получить смеси, составы которых определяются линиями ks ′ и ns ′′ , рис. 4 и 5. Если нагревать до 800 К смеси [(H 2 –CO 2 )– H 2 O] и [(H 2 O–CO)–CO 2 ]

разного состава, то можно получить водяной газ любого состава в области mnkt, рис. 2. При нагревании до 800 К паров воды в контакте с углеродом получается водяной газ, состав которого определяется точкой пересечения линии nd с изотермой 800 К. Если же нагревать до 800 К смеси (H2 – H2O) разного состава в контакте с углеродом, то получается водяной газ с составом, определяемым любой точкой на линии ms′′.

Зависимости расходов углерода y , s по реакциям газификации (3), (2) и общего количества газифицированного углерода ∑ n C = y + s при нагревании Н 2 О – C представлены в табл. 7 и на рис. 7. Углерод газифицируется только по реакции (3) и с повышением температуры интенсивность газификации углерода парами воды повышается. При температурах выше ~ 1100 К имеет место 100 % расход паров на газификацию. Образующийся при газификации оксид СО диссоциирует с образованием сажистого углерода, s < 0. При этом наблюдается хорошо известное повышение термодинамической стабильности СО при температурах выше 1100 К. Расчетами показано, что добавление в систему Н 2 О – C диоксида углерода кардинально влияет на состав получающегося водяного газа и на газификацию углерода. Например, в табл. 9 приведены результаты расчетов равновесных параметров систем

«Н 2 – Н 2 О – СО – СО 2 – С», получающихся при 900 К в «Н₂O (1 моль) – СО 2 ( d о ) – С» (варьировалось количество СO 2 при неизменном количестве Н₂О). На рис. 7 стрелками показано сравнение количеств газифицированного углерода при 900 К и 1 атм в системе «Н 2 О (1моль) – С» и «Н 2 О (1моль) – СО 2 (9 моль) – С»:

- при b _o / d o ^ да ( d o ^ 0) y ^ 0,7265, s ^ 0,2328, £ n C ^ 0,4937 моль;
- при b _o/ d _o ^ 0,1111 ( d _o ^ 9) y ^ 0,5769, s ^ -1,7982, £ n C ^ 2,3751 моль.

При соотношении в исходной системе d _о / b _о ≥ ≥ 0,845 / 1 диссоциация CO с образованием сажистого углерода не происходит, углерод начинает газифицироваться диоксидом CO 2 , а при d о / b о ≥ 3,448 / 1 количество углерода, газифицированного диоксидом CO₂, становится больше, чем парами воды.

В научной литературе принято количественно оценивать окислительные и восстановительные свойства газовой фазы кислородным потенциалом n o = RT In p о либо вели-

чиной lg( p _O , атм) [3, 4, 14, 15]. Расчетная

формула для lg( p _O , атм) получается из анализа равновесия реакций диссоциации H 2 О или СО 2 :

2H O =2H + O ,

2 2 2 (11)

A G y (11) = 492 230 - 108,24 ■ T ;

2CO =2CO + O ,

2 2 (12)

A_r G ^y (12) = 565 390 - 175,17 ■ T ;

lg[ P о₂ ,атм] = 2 ■ lg

^H V H2 7

+ lg K p (11) =

= 2 ■ lg

. H 2 O x_H

V H2 7

25708 T

+ 5,653;

Таблица 9

Параметры равновесия систем «Н 2 – Н 2 О – СО – СО 2 – С», получающихся при нагревании до 900 К исходных систем «Н 2 O ( b o ) – СО 2 ( d o ) – С», 1 атм

b о	1	1	1	1	1	1	1	1	0
d о	0	0,5	0,845	1	2	3	~ 3,448	9	9
y = n C (15)	0,7265	0,6635	0,6427	0,6360	0,6108	0,5990	~ 0,595	0,5769	–
s = n C (2*)	0,2328	0,0875	0	–0,0368	–0,2678	–0,4907	~ –0,595	–1,7982*	1,9436*
∑ n C = y – s	0,4937	0,5760	0,6427	0,6728	0,8786	1,0897	1,190	2,3751*	1,9436*
a , моль	0,7265	0,66346	0,6427	0,63598	0,6108	0,5990	~ 0,595	0,5789	–
b , моль	0,2735	0,33654	0,3573	0,36402	0,3892	0,4010	~ 0,405	0,4211	–
c , моль	0,2608	0,4884	0,6414	0,7096	1,1463	1,5804	~ 1,785	4,1754	3,8872
d , моль	0,2328	0,5875	0,8456	0,9632	1,7322	2,5093	~ 2,853	7,2018	7,0564
∑, моль	1,4936	2,0759	2,4870	2,6728	3,8786	5,0897	~ 5,638	12,3772	10,9436
V , л	110,2	153,2	183,54	197,3	286,2	375,6	416,1	913,4	807,6
x _H ₂	0,4864	0,3196	0,2584	0,2379	0,1575	0,1177	0,1055	0,0468	–
x H₂O	0,1831	0,1621	0,1437	0,1362	0,1003	0,0788	0,0718	0,0340	–
x CO	0,1746	0,2352	0,2579	0,2655	0,2956	0,3105	0,3166	0,3373	0,3552
x CO₂	0,1559	0,2830	0,3400	0,3604	0,4466	0,4930	0,5061	0,5819	0,6448
(lg p _O ₂ )	–23,76	–23,50	–23,42	–23,40	–23,30	–23,26	–23,25	–23,19	–23,14

^CO 2

lg[ P o₂ ^, ^атм] = ² • lg

+ lg Kp (12) = к XCO

Для любой сколь угодно сложной газовой смеси, в которой присутствуют СО 2 и Н 2 О, в том числе и для водяного газа, кислородный

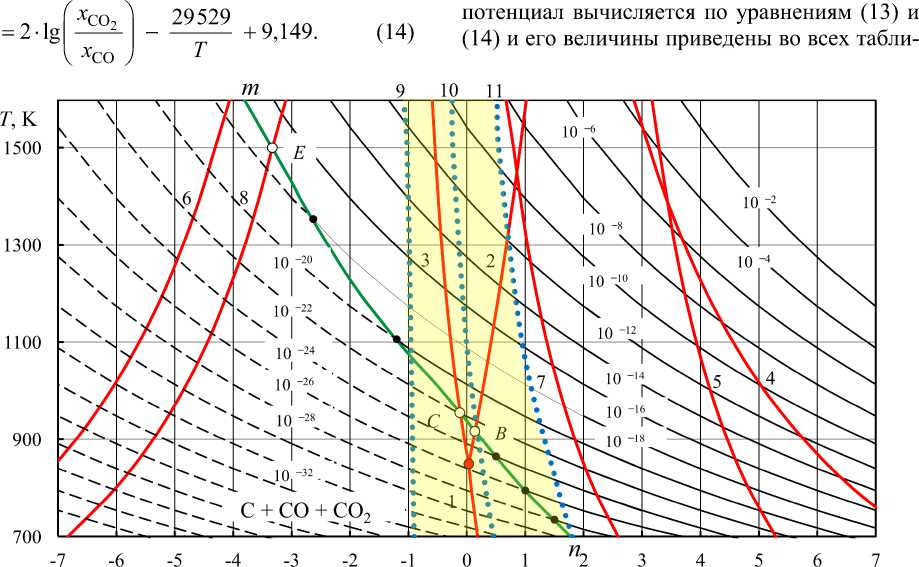
lg (XC02 ^ XCo)

Рис. 8. Номограмма « lg

^CO"

V xCO J

– p _O – T » для газовых смесей, содержащих СО 2 и СО, 1 атм

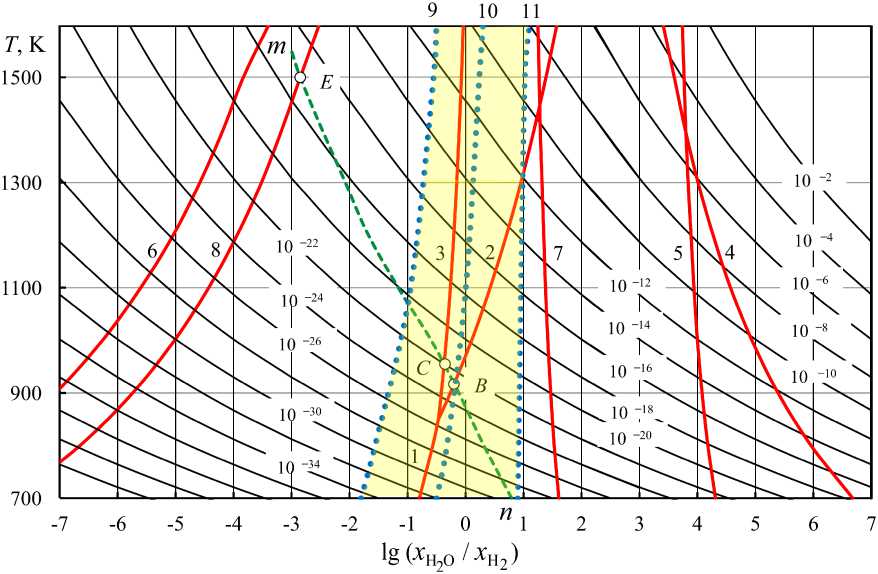
Рис. 9. Номограмма « lg

– pO – T» для газовых смесей, содержащих Н2О и Н2, 1 атм x H2O

x_H V ^H2

цах настоящей публикации, а на рис. 5 для примера представлена графическая информация о кислородном потенциале на концентрационном треугольнике H₂ – O₂ – C для 1000 К. Соотношение положения крайних точек изобар кислорода 1–5 в области II определяется константой равновесия реакции водяного газа:

K 1 = 'CO x . , x c. = _K 1 , x H (15) x H ₂ x H ₂ O x CO ₂ x H ₂ O

Результаты расчетов lg( p _O2 ) по уравнениям (13) и (14) могут быть представлены и номограммами, предложенными более полувека назад [16] и незаслуженно забытыми (рис. 8 и 9). Линия nm на этих рис. 8, 9 определяет условия диссоциации CO с образованием сажистого углерода или параметры равновесия водяного газа с присутствующим в качестве самостоятельной фазы углеродом. Номограммы позволяют определять параметры газовых смесей (Н 2 О – Н 2 ), (СО 2 – СО) и (Н 2 – Н 2 О – СО – СО 2 ), при которых возможно восстановление оксида металла. Для примера на рис. 8 и 9 линиями 1–8 показаны параметры восстановления Fe 3 O 4 до Fe и до FeO, FeO до Fe, Cu 2 O до Cu, Mn 3 O 4 до MnO, MnO до Mn, CoO до Co и Cr 2 O 3 до Cr. Положения этих линий определяются расчетом констант равновесия соответствующих реакций восстановления либо по упругостям диссоциации оксидов [17].

Список литературы Термодинамический анализ системы H2 - O2 - C

Есин, О.А. Физическая химия пирометаллургических процессов / О.А. Есин, П.В. Гельд. - Изд. 2-е. - М.: Металлургиздат, 1962. - Ч. 1.
Гольдштейн, Н.Л. Водород в доменном процессе / Н.Л. Гольдштейн. - М.: Металлургия, 1971. - 208 с.
Попель, С.И. Теория металлургических процессов: учеб. пособие для вузов / С.И. Попель, А.И. Сотников, В.Н. Бороненков. - М.: Металлургия, 1986. - 463 с.
Теория металлургических процессов: учебник / Д.И. Рыжонков, П.П. Арсентьев, В.В. Яковлев и др. - М.: Металлургия, 1989. - 392 с.
Дигонский, С.В. Роль водорода в восстановлении оксидов металлов твердым углеродом / С.В. Дигонский, В.В. Тен // Альтернативная энергетика и экология. - 2009. - № 11 (79). - С. 45-55.
Дигонский, С.В. Карботермическое восстановление оксидного сырья в неравновесных химических системах / С.В. Дигонский // Технология металлов. - 2008. - № 8. - С. 3-7.
Патент RU 2111271 С1. Способ получения металлов из их сульфидов / С.В. Дигонский, Н.А. Дубинин, Е.Д. Кравцов. - Заявл. 22.10.96; опубл. 20.05.98.
Патент RU 2033431 С1. Способ получения металлов / В.В. Дигонский, С.В. Дигонский, В.Е. Горбовский. - Заявл. 02.04.91; опубл. 20.04.95.
Строкина, И.В. Изменения окислительно-восстановительных свойств газовой фазы системы C - O2 - H2 / И.В. Строкина, Н.Ф. Якушевич // Изв. вузов. Черная металлургия. - 2011. - № 6. - С. 3-5.
Якушевич, Н.Ф. Определение параметров окислительно-восстановительных процессов в системе Fe - C - O2 - H2 / Н.Ф. Якушевич, И.В. Строкина, О.А. Полях // Изв. вузов. Черная металлургия. - 2011. - № 8. - С. 13-18.
Гришин, А.М. О несоответствии кинетических закономерностей термодинамическим предпосылкам реакций газификации углерода H2O и CO2. / А.М. Гришин, В.К. Симонов, И.С. Щеглова // Изв. вузов. Черная металлургия. - 2013. - № 7. - С. 64-67.
Дубинин, А.М. Оптимальные параметры паровой газификации углей в газогенераторе с заторможенным циркуляционным псевдоожиженным слоем / А.М. Дубинин, С.П. Маврин // Изв. вузов. Черная металлургия. - 2016. - Т. 59, № 11. - С. 773-780.
Перспективы использования политопливного газогенератора в практике работы доменных цехов / Г.С. Подгородецкий, А.А. Третяк, В.Б. Горбунов, Л.А. Полулях // Изв. вузов. Черная металлургия. - 2016. - Т. 59, № 12. - С. 879-885.
Термодинамика восстановления железа из оксидов / Г.П. Вяткин, Ю.С. Кузнецов, Г.Г. Михайлов, О.И. Качурина. - Челябинск: Издат. центр ЮУрГУ, 2017. - 346 с.
Михайлов, Г.Г. Термодинамика металлургических процессов и систем / Г.Г. Михайлов, Б.И. Леонович, Ю.С. Кузнецов. - М.: Издат. Дом МИСиС, 2009. - 520 с.
Muan, A. Phase eqilibria among oxides in steelmaking / A. Muan, E.F. Osborn. - New York: Pergamon Press Limited, 1965.
Казачков, Е.А. Расчеты по теории металлургических процессов / Е.А. Казачков. - М.: Металлургия, 1988. - 288 с.

Еще

Статья научная