Термодинамический анализ системы железо-хромазот

Железохромовые сплавы являются основой жаростойких и жаропрочных сплавов. Специфические свойства этих сплавов в значительной степени определяются содержанием в них азота. Повышенное содержание азота в расплаве в процессе охлаждения и кристаллизации металла приводит к образованию нитридных и карбонитридных включений, которые могут оказывать значительное влияние на размер зерна, снижать окалиностой-кость, пластичность и живучесть сплавов, а в случае неблагоприятной формы и расположения могут служить причиной хрупкого разрушения металла. Поэтому экспериментальное и теоретическое исследования образования равновесных фаз в этих сплавах и, в частности, определение взаимной растворимости компонентов в этих сплавах имеет первостепенное значение.

При термодинамическом описании металлических сплавов, содержащих азот, использована модель регулярного раствора Хиллерта - Стеф-фансона [1], которая может быть применима к системам M1-M2-N, содержащим два растворителя (Mi и М^ с образованием раствора замещения, и одно вещество (N), образующее растворы внедрения. Таким образом, вакансии (Г) в подрешетке внедрения рассматриваются как дополнительный компонент системы.

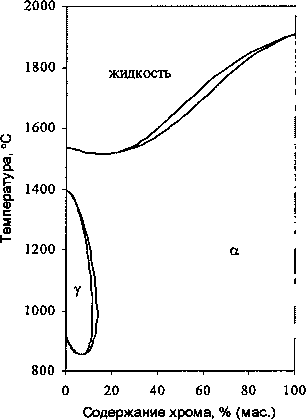
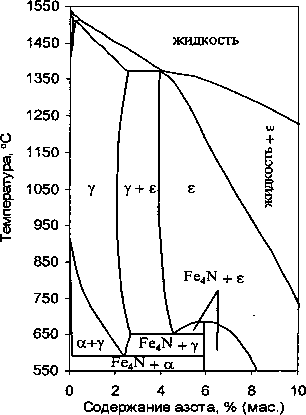
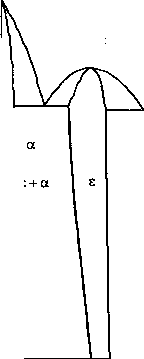
При термодинамическом анализе фазовых равновесий в трехкомпонентной системе Fe-Cr-N, необходимо знать свойства веществ, образующихся в двухкомпонентных системах железо - хром, железо-азот и хром-азот. Термодинамический анализ системы железо-хром проведен в исследовании [2] (рис. 1, а). Данная система характеризуется наличием в твердом состоянии двухфазной области у + а. В сплавах системы Ме-^ возможно образование твердых растворов и фаз внедрения £ гексагональной структуры на основе химического соединения Ме^ (рис. 1,6, в). Система хром -азот характеризуется образованием нестехиометрического нитрида хрома структуры г.ц.к. [3,4].

Система железо-хром-азот была предметом многочисленных экспериментальных и теоретических исследований [5-7]. Установлено, что в этой системе образуются трехкомпонентный жидкий раствор и тройные твердые растворы внедрения структуры о.ц.к. (а), г.ц.к. (у) и г.п.у. (с). Взаимодействие компонентов растворов приводит к образованию нитрида хрома нестехиометрического состава (Сг, Fe)Ni_x.

Жидкий расплав. Молярная энергия Гиббса гомогенного трехкомпонентного сплава задается уравнением

Gm ^{= х}Сг^Сг ^{+ x}Fe^Fe ^{+ x}N^N ⁺ ^^(^хСг ^Х^ +

+xFe lnxFe +xN hxN)+xCrxFeZCr Fe +

+xCrxNZCrN +xFexNZFe>N +xCrxFexN x

^x(^xCr^Cr,Fe,N ^{+ x}Fe^Cr,Fe,N ^{+ x}N^Cr,Fe,N).     (1)

где x, - молярные доли компонентов раствора; G° - энергия Гиббса чистого компонента; R -

жидкость

1800 -

1600 -

1400 -

1200 -

e + CrN

CrN

0          10          20

Содержание азота, % (мае.)

в)

Рис. 1. Диаграммы состояния двухкомпонентных систем Fe-Cr (a), Fe-N (б) и Cr-N (в)

универсальная газовая постоянная; Т - абсолютная температура; Lij - температурно-зависимые параметры модели, значения которых выражали полиномами Редлиха-Кистера:

Ь_у = Т.1^х,-х^ .                 (2)

77=0

Парциальные молярные энергии Гиббса (химические потенциалы) могут быть вычислены по уравнению [8]:

где 6^ - символ Кронекера (8^ = 0 при i^j и 8,у =1 при i = j\

Значения параметров модели приведены в таблице

Твердые растворы внедрения (а, у, s) и CrN. В таких растворах металлические вещества (железо и хром) образуют подрешетку замещения, а азот и вакансии (Г) - подрешетку внедрения. Тогда твердый раствор внедрения можно представить общей формулой (Cr,Fe)_o(N,P)_c. Образование такого раствора можно представить смешением гипотетических соединений Л_ОК_С, А_аУ_с, В^_с и В_аУ_с, а молярную энергию Гиббса такого «четырехкомпонентного» раствора уравнением

G_m⁼ УСгУу^СгУ ⁺ УСгУ^Ст:^ ⁺ УЕеУу^еУ ⁺

⁺УреУк^Ре^ ⁺ ^ Л ^а(УСг ^ УСг ⁺ Уре I¹¹ УЕе ) ⁺

с(№ lny_N +Уу lnya + G™ ⁶ +СГ .      (3)

где

Gm^{6 =} УСгУРе (yN^Cr,Fe:N ⁺ Уу^Сг,Ре:У ) ⁺

+УгУи (УСг ^Cr:P,N + Уре ^e:K,N )•            W

Слагаемое G^ определяет магнитную составляющую энергии Гиббса. Её определение следует из данных, приведенных в таблице. Параметры L вычисляются по формуле (2), а состав твердого раствора определяется мольными долями веществ в каждой подрешетке:

yPe = XFe/(l - XN) ИуРе + yCr = U              (5)

Ус = HMl - XN) иУы + УК = 1,        (6)

где а и с числа межузельных промежутков в металлической подрешетке. Их значения приведены в таблице.

В уравнении (4) в подстрочных индексах запятая разделяет компоненты в одной подрешетке, а двоеточие означает различие подрешеток.

Парциальные молярные энергии Гиббса гипо тетических компонентов твердого раствора определяются по формуле [9]

С -С I ^9Gm I ^    V   „ ^HL П\

Gi:j Gm+^~ + ~^--L  Ук^—Л')

®Vi 9Vj к=Ст,¥е,М,У ^Ук где z иу — элемент замещения и внедрения соответственно. Парциальные величины реальных компонентов определяются следующим образом:

^z ⁼ ^1У» ^N ⁼ ^/:N ~^г.У-

Термохимические данные и температурнозависимые параметры модели, необходимые для расчета, получены при оптимизации экспериментальных данных и приведены в таблице [5-7].

Графическая зависимость результатов расчета по полученным соотношениям представлена на рис. 2 в виде изотермических сечений в интервале температур 1600... 1000 °C. Из приведенных графических зависимостей следует, что при 1600 °C (рис. 2, а) первично кристаллизующими фазами будут твердые растворы а, е(Сг) и химическое

Термодинамические параметры системы хром-железо-азот

Фаза	Параметр, Дж/моль	Примеч.
Жидкий расплав (Ж)	С°(ж) _! / 2G^ = 29950+59,027 б#ж) - G^ = 24335,93 -11,427+2,37615 ■ 10“2177 G^1 -Я2°98 =-16459 + 335,618-7-5071п7 G^"G^ =12040,17-6,558437-3,6751551 10-2177 Gp^ -^298 =-10839,7+291,3027 - 467In 7 £^=-161800-16,117 ^ = 65508 /^ =-19930-12,017 £^е =-14550+6,657 гЖж) _ ^Cr,Fe,N “	7<2180K 7>2180K Т<1811К 7>1811 К
О.ц.к. -твердый раствор (а); а=1, с=3	со(оцк) _ яод8 = _885 ^93 + J 57,487 _ 26; 90871п7 _ -0,0018943572 -1,47721 •10"673 +1392507’1 G^ - Н298 = -34864+344,187 - 5071п7 - 2,88526 • 1032 7~9 G^ -^298 =+1224,83 + 124,1347-23,514371п7- -0,0043975272 -5,89269 10""873 + 77358,57"1 G^ -^298 = -25384,451+299,312557-4671п7 +2,2960305-10317"9 G”^ - G^ - 3 / 20^ =311870+29,127 g№ - G^ - 3 / 2G^ = 93562+165,077 Z,^^ =-2000007 L^y =20500-9,687 7^n = -799379 + 2937 G“ar=^ln(P+l)/(t) ,. .    1 Г .    79    158 (1   ,Y t4   t10   t16 )1 tA    140p 497^/2  Д2  45  200J 1 Г^-5 ^-’5 ^-25 1 /(t) = -------, где Л[1О 315 1500] , 518 Г 790 (1 Л1     .. 1125|_ 497^р JJ Тс = -31 l,5yCr +1043yFe +yCr7Fe[1650 + 550(yCr -yFe)] Р = -0,008yCr + 2,22yFe - 0,857cryFe	7<2180К 7>2180К 7<1811К 7>1811К т<1 т>1
При отрицательных величинах Тс и р, их значения следует поделить на -1

Г.ц.к. -твердый раствор (у) и «CrN»; а=1, с=1	G^ -G^) = 7284 + 0,163 7 G^ -G^ = -1462,4 + 8,2827-1,1571n7+6,4-10"472 Gj^ - Я298 = -27098,266+300,252567 - 467In 7+2,78854 • 1031 T9 G^ -G^ -1/20^ =-124460 + 142,167 - 8,571n7 25000 G^ - С°У -1 / 2G*33) = -37460+375,427 - 37,67 In 7 Z^K = 20000 J®v =-26150 Z^v =10833-7,4777 ®:V = 14Ю 7^n = -128930 + 86,497 ^n =24330 ^CrJcN,V =-162516	7<1811K 7>1811К
Г.п.у. -твердый раствор (s); а=1, с=0,5	G^ "GCr^ =4438 G^ -Я^98 = -2480,955 + 136,72557 - 24,664371n7- -0,0037575272 - 5,89269 • 10"8 73 + 77358,57"1 G^-H^g = -29341,65 + 304,562067 - 4671n7 + 2,78853995-10317"9 G^l -G$°^ -l/4G°(ro) =-65760 + 64,167-3,9371n7 G^ -G^ -IMG*33) = -12015+37,987 Lc^y =21120-10,617 7'сти=-6204 tiy =10345-19,717 7^)^ =-11130 + 11,847 Z,^K =10833 - 7,4777 1^^N =12826-19,487	7<1811 7>1811
N2(ra3)	1/2G*33) -Я2°98 =-3750,675-9,454257-12,78197 ln7- -0,0017668672 + 2,680735-10-9 73 -323747"1 1/2G*33) -Я298 =-7358,85 + 17,20037-16,369971n7- -0,0006510772 +3,0097-10"873 +5630707”1	7<950 7>950

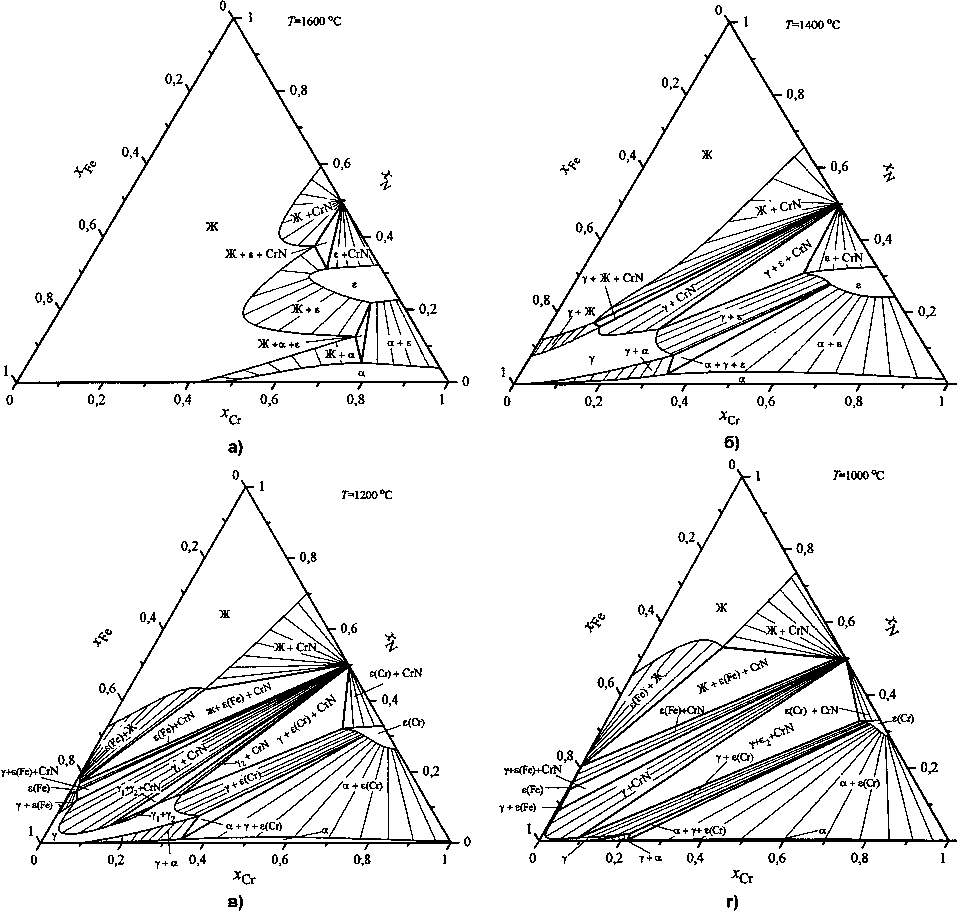
Рис. 2. Изотермические сечения системы железо-хром-азот при температурах (°C): 1600 (а), 1400 (б), 1200 (в) и 1000 (г)

соединение CrN. Комплекс фаз, образующихся при кристаллизации жидкого расплава, графически представлен на рис. 3 линиями трехфазного равновесия с участием жидкости. Области между кривыми определяются как политермические поверхности растворимости компонентов в расплаве, равновесном с одной из кристаллизующихся фаз.

При температуре 1400 °C (рис. 2, б) эти же фазы равновесны аустениту, область гомогенности которого при снижении температуры уменьшается. При этом изменяется также состав и количество равновесных неметаллических фаз.

На изотермических сечениях при заданной концентрации одного из компонентов можно установить последовательность фазовых превращений и определить количественные соотношения равновесных фаз. Однако наиболее представительными и удобными для анализа являются политермические разрезы при постоянной концентрации одного из компонентов. На рис. 4, а приведено такое поли

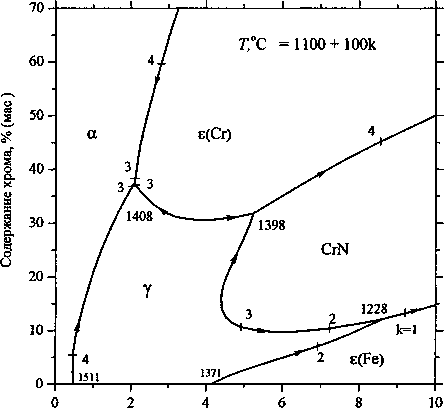
Содержание азота, % (мае.)

Рис. 3. Диаграмма трехфазных равновесий с участием жидкости

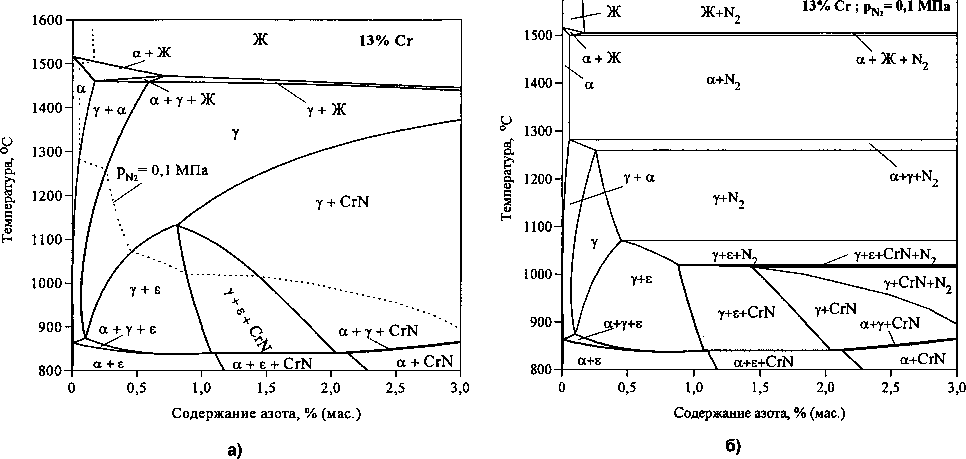
Рис. 4. Политермические разрезы диаграммы состояния системы железо-хром-азот: 13 % Сг (а), 13 % Сг и р(М2) = 0,1 МПа (б)

термическое сечение, соответствующее содержанию хрома в металлическом сплаве 13 % (мае.). Диаграмма на рис. 4, б отвечает тому же политер-мическому разрезу диаграммы Fe-Cr-N, когда давление азота в газовой фазе постоянно и равно 0,1 МПа. При этом реализуются трехфазные равновесия с участием газовой фазы.

Выводы. Проведен термодинамический анализ и изучены фазовые равновесия в трехкомпонентной системе железо-хром-азот. Рассчитаны и построены изотермические сечения в интервале температур 1600... 1000 °C. Рассчитана проекция поверхности ликвидуса и установлен комплекс первично кристаллизующихся фаз. Результаты расчета представлены также в виде политермических разрезов с постоянным содержанием хрома и одинаковым значением активности азота в системе.

Работа выполнена в соответствие с научной программой Федерального агентства по образованию - «Развитие научного потенциала высшей школы (2009-2010 гг.)», код проекта - 713 и при поддержки РФФИ, грант № 08-08-00416.