Термодинамический анализ системы железо-сера

Эффективность процессов, связанных с удалением серы из стали, является актуальной в черной металлургии. При анализе реакций десульфурации жидкого расплава основополагающей является система железо-сера, а также комплекс равновесных фаз, образующихся в этой системе.

При термодинамическом анализе системы Fe-S использована подрешеточная модель М. Хиллерта [1-3]. При этом предполагается квазирегулярная структура жидкого расплава, когда в подрешетках, образованных металлом и серой, имеются вакансии ( Va ). Так что структуру такого расплава можно отобразить общей формулой (Fe, Va 1)(S, Va 2).

В рамках этой модели молярная энергия Гиббса может быть представлена уравнением

7^ ж _ Г’О(ж) । Г’О(ж) I Г’О(ж) I G m = ^yVa1 ^yVa 2 G Va 1: Va 2 + y Fe y Va 2 G Fe Va 2 + ^yVa 1 y S G Va 1S +

⁺ У Fe y s G oes') ⁺ RT ⁽ V ln V ⁺ У Fe In У Fe ⁺ y Va 2 In y Va 2 ⁺

ж(Va2)r'(S)

⁺ У S In У s ) ⁺ y Va 1 У Fe y Va 2 L Va 1Fe ⁺ y Va 1 У Fe y s L Va 1FeS ⁺

,                tж(Va 1) ,               r'(Fe)zi\

+yVa2УSyVa 1 LVa2S + yVa2 УSУFeLVa2S , где yi - число мест в подрешетке; yFe + yVa 1 = = yS + yVa2 = 1; Lkj - температурно-зависимые параметры модели, значения которых выражаются полиномами Редлиха-Кистера:

Т ⁽ k ) — r^o( k ) . r¹⁽ k )(_т Y Air² k )(_Y V 'l²

L ij = L ij ⁺ L ij ⁽ x i - x j ) ⁺ L ij ⁽ x i - x j ) . ⁽²⁾

В данной системе образуется нестехиометрический сульфид железа FeS x (пирротин). В исследовании [3] предполагается, что в области низких содержаний серы концентрация вакансий ( y_Va 1 ) в жидком железе невелика и ими можно пренебречь. Для сульфидного расплава, наоборот, считается небольшой концентрация y_{Va 2}. Их концентрация существенно возрастает вблизи области существования пирротина.

Парциальные молярные энергии Гиббса гипотетических компонентов бинарной системы вычисляли по формуле

Г      . ^д G m ^{д G} m _v  д G_m

Gi:j = Gm +^+ ,--LУк -- дyi    дyj    к     дyk

( к = Fe, Va 1,S, Va 2).

Тогда в соответствии с уравнением (1) парциальные молярные энергии Гиббса компонентов расплава, обогащенного железом (верхний индекс (Fe)), будут иметь вид:

G ¹ '(Fe) х//~|О(ж) /~<о(ж) x , //~<о(ж) /~<о(ж) х , S ⁽ ) = ^{(1 -} У Fe ⁾⁽ G ValS - G ValVa 2 ) ⁺ У Fe ^{( G} Fes ) ^- G FeЩ2 ) ⁺

+ RT ln[( y s /(1 - y s)] - y Fe (1 - У Fe ) L VV F^ +

+ У Fe (1 - 2 У s ) L VI21 + У Fe (1 - У Fe )(2 У Fe - 1) L VV^ +

+ У Fe (1 - У Fe ) ^ (1 - 2 У Fe ) L^ Fe + (1 - У Fe )[1 - 6 y s (1 - У д )] Х

■ L VV^ + У Fe [1 - 6 У s (1 - y s )] L VV FeS ;                 (4)

^G Fe Va 2 = ^G Fe: Va 2 ^{+ (1 - y} Fe ) ^y S ^{( G} FeS ^{- G} Fe Va 2 ⁺

+ G Va 1S + G Va 1Va 2 ) + RT ln[ У Fe (1 - У s )] +

^{+ (1 - y} Fe ^{)(1 - y} S ^{- y} Fe ^{+ 2 y} Fe ^y S ) L VV Fe ⁺

+ y s (1 - У Fe )(1 - 2 y Fe ) L VS Fe + y s (1 - У Fe )(2 y s - 1) L Xf +

^{+ y}S ^{(1 - y} S ^{- y} Fe ^{- 2 y} Fe ^y S ) L Va2S ^{+ y} S^{[(1 - 3 y} S ^{+ 2 y} s ) ^{+ + y} I e^{(6 y} s ^{- 6 y}S ^{- 1)]} L as ^{+ y} s^{(1 - y} i e^{)(6 y} s ^{- 6 y}S ^- 1) L VV^a s^{2) + + y} S^{(1 - y} Fe^{)(6 y} Fe ^{- 6 y} Fe ^{+ 1)} L V SlFe ^{+ (1 - y} Fe^{)[ y} Fe^{(1 - 2 y} Fe ) ^- - (1 - У s )(6 У Fe - 6 y Fe + 1)] C^.                 (5)

В случае расплава, обогащенного железом, содержание серы в подрешетке рассчитывается из соотношения y _s = x _s /(1 - x _s).

Аналогично были определены парциальные характеристики и расплава, обогащенного серой.

Энергия обмена вакансий ( G V _{a 1: Va 2}) в различных подрешетках также рассчитывалась по формуле (3). При этом было получено соотношение:

Лукоянова С.В., Леонович Б.И., Дильдин А.Н., Вахитова Е.Р.

Термодинамический анализ системы железо–сера

ж    o(ж)o(ж)o(ж)o(ж)

G Va 1Va 2 = G Va 1Va 2 ⁺ y Fe y S⁽ G Va 1S ^{+ G} Fe Va 2 G Va 1Va 2

- G _F^) ) + RT ln[(1 - y Fe )(1 — y s )] + y Fe [(1 - y Fe ) y s +

^{+ y} Fe⁽¹ - ^y s) ^LVa1 Fe) ^{+ y} Fe ^y S^{(2 y} Fe - 1) L a Fe ⁺

^{+ y} S^{[ y} Fe ⁽¹ - ^y s) ^{+ y} S⁽¹ - ^y Fe^)] L a S ) ⁺

^{+ y} S ^y Fe (2 ^y S - 1) L Va 2S ^{+ y} Fe ^[(1 - ^y Fe ) ^y S ⁽¹ - ^{2 y} Fe ) ⁺

+ (3 - 4 y _{F e})] L^ a ,²_e) + y_sy _Fe [6 y _Fe (1 - y _Fe) - 1] L ^ _e +

Fe Va 1Fe S Fe Fe Fe        Va 1Fe

+ y s [ y Fe (1 - y s )(1 - 2 y s ) + (1 - y Fe ) y s (3 - 4 y s )] <£) + ⁺ y Fe y S ⁽⁶ y S ^{- 6} y S ^- 1) L VFS ,                       ⁽⁶⁾

где G Va 1 Va 2 ^{- G}Va 1 Va 2 = 0 •

В случае твердых растворов внедрения при достаточно малых значениях концентрации серы молярная энергия Гиббса и парциальные энергии компонентов раствора могут быть рассчитаны в предположении регулярного раствора [3]:

G m = x Fe ^G Fe: Va ⁺ x S ^G I^?e:S ⁺ RT ⁽ x Fe ^ln x Fe ^{+ x} S ^ln x s ) ⁺

+ X Fe X S L Fe: Va + G m ,                              (7)

В этой формуле магнитная составляющая энергия Гиббса определяется формулой

G m M^ar = RT ln( p + 1) • f ( t ),                     (8)

где p ^Fe = 2,22; t = T / T_c ^Fe; T^ = 1043 K - температура Кюри железа;

f ( t ) = 1 - 0,9053 t ³ - 6,8 ^ 10 ^{- 3} t ⁹ - 1,53 t ¹⁵ при t <1;

f ( T ) = - 6,417 • 10 ^{- 2} t^{- 5} - 2,037 • 10 ^{- 3} t^{- 15} - 4, 278 t^{- 25} при T <1.

Результаты расчета растворимости серы в твердых и жидких растворах представлены на рис. 1.

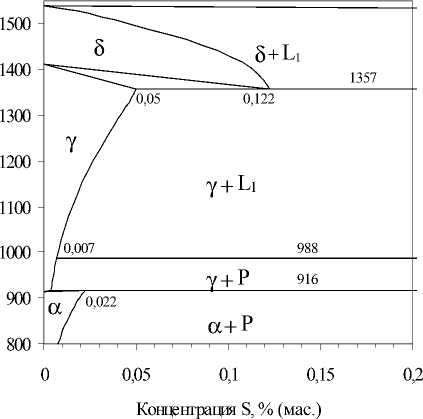
Рис. 1. Растворимость серы в твердых растворах системы Fe–S

Термохимические параметры системы железо–сера [3]

Фаза	Параметр, Дж/моль
Жидкость (Ж)	G Fe Va 2 - G Fe(ГЦК) =- 11274 + 163,878 T - 22,03 T ln T + 4,1755 • 10 - 3 T 2 G Va S - 1 G So2 (ra3) =- 65357 + 165,396 T - 13,513 T ln T G 0eS - G 0е (ГЦК ) - 1 G s'(газ) =- 157578 + 200,119 T - 19,252 T ln T FeS Fe 2 S2 o( Va 1)     o( Va 2) L Va 2Fe = L Va 1S = 1001 L Va FS) = 31761 - 9,202 T Z V FS) = 10761 + 0,477T L V2.Fe = 79779 - 45,139 T L VS2Fe = 57510 - 17,082 T
Пирротин (Р)	G FeS - G Fe (ГЦК) - 1 G so2 (ra3) =- 150957 + 15,076 T + 5,598 T ln T G Va S - -2 G So2 (ra3) = 6433 + 145,376 T L VaFe =- 126374 - 69,27 T
ГЦК ( Y )	G '(ГЦК) - 1 g '(газ) =- 30000 + 50 T S           2 S 2 L ™ = 11442 - 24,855 T
ОЦК ( a )	G FeОЦК) - G FeГЦК) = 1462,4 - 8,282 T + 1,15 T ln T - 0,00064 T 2 G '(оЦК) - 1 g ' (газ) = - 31000 + 50 T S           2 S 2 2 (ОЦК) =- 27053 - 8,18 T

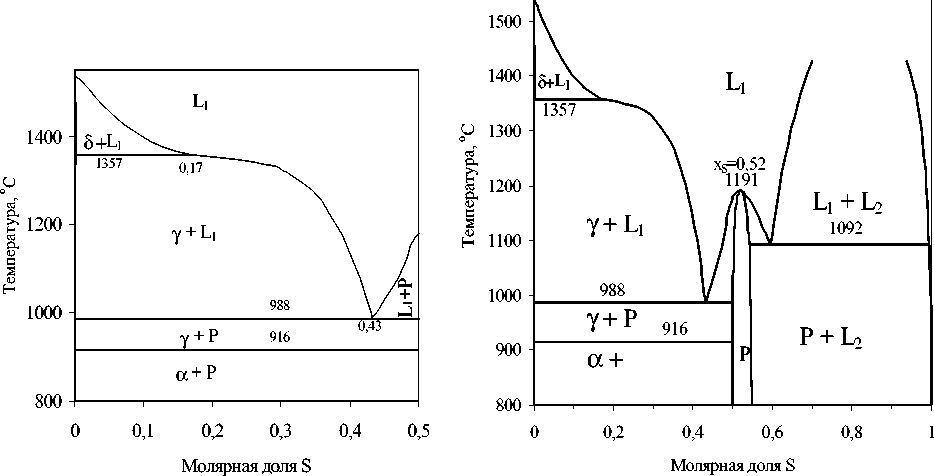
Рис. 2. Диаграмма состояния системы Fe–FeS

Рис. 3. Диаграмма состояния системы железо–сера

С позиции подрешеточной модели были также рассчитаны термодинамические свойства пирротина (Р). При этом парциальные молярные энергии Гиббса представлены уравнениями:

G S ^P = G V ^o a ⁽S ^{P )} + RT ln(1 - y Fe ) + y F²e L ^S V ⁽ a^P F⁾e ;

G F ^P e = G F^oeS - G V ^o a S + RT ln[ y Fe /(1 - y Fe )] - (9)

- (2 y Fe - 1) L S _V ( _a ^P F)e .

Параметры модели определены в соответствии с экспериментальными данными активности серы в пирротине [3]. Термохимические данные, использованные в расчете, представлены в таблице.

Графическое представление равновесных фаз в полусистеме Fe–S показано на рис. 2. В этом интервале концентраций имеют место два нонвари-антных превращения с участием жидкого расплава: перитектическое (при температуре 1357 °С) и эвтектическое (при 988 °С).

На рис. 3 по результатам расчетов приведена диаграмма состояния системы железо – сера.

Работа выполнена в рамках реализации научной программы Министерства образования и науки РФ «Развитие научного потенциала высшей школы (2009–2011 годы)», код проекта – 713 (10909).