Термодинамический анализ технологических процессов в системе охлаждения поршневых двигателей

Теплообмен между рабочим телом и стенками цилиндра дизеля влияет, с одной стороны, на рабочий процесс: на характеристики изменения давления, расход топлива, температуру выпускных газов, работу газовой турбины. Последнее оказывает влияние на расход воздуха, коэффициент избытка воздуха и температуру цикла. С другой стороны, сам теплообмен является следствием протекания рабочего процесса и определяет локальные термические нагрузки на основные узлы и детали, теплонапряженное состояние которых зачастую является причиной ограничения уровня форсирования дизеля.

Поэтому в настоящее время, когда остро стоит проблема дальнейшего форсирования и совершенствования дизелей, на повестку дня ставится вопрос о разработке теории, позволяющей решать задачи локального теплообмена в цилиндре дизеля. Следует отметить, что вопросам исследования теплопередачи в поршневых двигателях в течение всей истории их развития не уделялось должного внимания. Достижение современной теплотехники – использование методов неравновесной термодинамики и теории нелинейной термодинамики – не нашли широкого применения в исследовании теплопередачи в современных форсирован- ных дизелях.

Для глубокого изучения исследования рабочего процесса необходимо иметь закономерности, определяющие теплообмен между рабочим телом и стенками цилиндра на любом участке цикла с учетом потери теплоты в системе охлаждения. В оптимально спроектированной системе охлаждения двигателя закон регулирования должен представлять собой такую зависимость температуры охлаждающей жидкости tB от нагрузки двигателя, при которой на каждом нагрузочном режиме организуется экономически оптимальное сочетание расхода топлива, скорости износа и расхода смазочного масла.

При установленном оптимальном тепловом состоянии двигателя общая картина теплоотдачи от рабочих газов в стенки цилиндра и головки двигателя достаточно сложна. Это обусловлено сложной зависимостью теплоты, передаваемой системе охлаждения, от температуры газов, коэффициентов теплопередачи и параметров, характеризующих технологический процесс в системе охлаждения. Следует добавить, что в указанных условиях, согласно второму закону термодинамики, охлаждающая жидкость, как термодинамически открытая система, сопровождается стремлением ее структу- ры к некоторому предельному состоянию, достигая как бы термодинамического равновесия.

Из термодинамики известно, что при описании открытых систем ведущую роль играет энтропия, так как это единственная функция, позволяющая различить неравновесные и равновесные процессы. А показателем необратимости термодинамических процессов систем является производство (возникновение) энтропии. Тогда задача оптимальной в термодинамическом смысле организации физикохимических процессов в охлаждающей системе ДВС состоит в том, чтобы выбором температур, давлений и химических потенциалов взаимодействующих подсистем, а также коэффициентов в уравнениях кинетики добиться минимума возникновения энтропии (диссипации) при заданной интенсивности потоков.

Производство энтропии, характеризующее необратимость процессов, равно среднему значению скалярного произведения вектора обобщенного потока J j на вектор обобщенных сил X j [2]: tm

5 = - j^ Jj ( u 1 , u 2)• Xj ( uj , u 2 j ) dt .

t 0 j =1

(1) где u ij - параметры процесса.

В этом случае условие минимальной диссипации технологических процессов в рассматриваемой термодинамической системе сводится к форме: tm

⁵ = ;jZ ^J j ⁽ u i, u 2 ^)х-    ₍₂₎

t 0 j =1                     ^{v 7}

... х X j ( u₁ j , u ₂ j ) dt -> min.

Из общего термодинамического уравнения Гиббса следует, что для открытой системы с переменным числом компонентов ОЖ при ее локально- равновесном состоянии скорость изменения энтропии будет выражаться уравнением

[1]:

dS-1 (dU+р dV) _ Tdi±i , (3) dt T dt dt T dt где р - равновесное давление; U - полная внутренняя энергия ОЖ; цi— химический потенциал i- го компонента ОЖ; ni - число молей i-го компонента; V - объем системы.

Из выражения (1) следует, что в открытой системе локальную энтропию можно представить в виде суммы двух слагаемых. Первое из них обусловлено обменом веществ и энергии с внешней средой - d e S (поток энтропии), а второе -производством энтропии - d i S необратимыми процессами внутри самой системы. С учетом этих пояснений получаем:

dS d S d S

— + —, (4) dt dt dt где: dgSfdr , diSIdT - соответственно скорости изменения обратимой и необратимой частей энтропии системы.

В охлаждающей системе (ОС) при теплообмене в зависимости от времени течения внутрицилиндровых процессов возможны как приток, так и отток энтропии, следовательно, производство энтропии за счет теплообмена со стенкой цилиндра может иметь любой знак. В системе одновременно идет также отток энтропии за счет теплообмена с окружающей средой через радиатор. Однако в целом суммарная энтропия за счет теплообмена будет иметь положительный знак, и определяться энтропийным равновесием, значение которого зависит от степени открытости системы и однозначно меняется с изменением степени воздействия внешней среды на ОС.

Рассматриваемая система обменивается с внешней средой не только энергией, но и веществами и информацией, что обусловлено физикохимическими процессами в ОЖ. Измене- ние при этом энтропии diS во времени

происходит вследствие как оттока, так и

притока энтропии вместе с компонентами теплоносителя и производства энтропии s вследствие неравновесных физикохимических процессов, происходящих внутри самой системы, и уравнение баланса производства энтропии имеет следующий вид [2]:

dS-^-^^*!—«•). (5)

dt j          j Т       j Tj где gj – интенсивность j-го материального потока; hj – удельная энтальпия; хdj – концентрация в потоке j- го вещества; qj – интенсивность j – го потока тепла; i – стехиометрический коэффициент реакции; w – скорость - й химической реакции; N (t) – мощность, отбираемая от рабочего тела в момент t.

Производство энтропии, возникающее вследствие теплопроводности стенки цилиндра двигателя, имеет форму: dS      1

i ,   =--y( q^' gradT ),          (6)

dt       _T ²

Если рассмотреть процесс фазового перехода какого-либо дифференциального объема теплоносителя за стенкой

цилиндра двигателя как неравновесный термодинамический процесс, то количество теплоты, подведенной от стенки цилиндра к этой открытой макросистеме при изменении ее состояния, согласно

второму закону термодинамики, может быть представлено в следующей форме:

Q ( s ,ц)= J jp „„ r

V пж T V

—dVdt = ... d

dе s  dis dd

d V-d t,

где Т – абсолютная температура охлаждающей жидкости; пж – массовая плотность двухфазной ОЖ; V – объем; –

где q – суммарный тепловой поток, воспринимаемый зеркалом цилиндра.

Суммарный тепловой поток q складывается из следующих нагрузок: тепловой, воспринимаемой непосредственно от газов q г и тепловой – от трения о зеркало цилиндра юбки поршня q пор и поршневых колец q кол 3 .

Количество теплового потока,

время.

С другой стороны, в соответствии с первым законом термодинамики для таких открытых систем количество теплоты, участвующей в бесконечно малом процессе тепломассообмена ОЖ, определяется выражением [1]:

N

5 Q = d Н vdpp-^ k_k dn_k ,

Н к

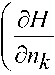
, v P , T , n -

k 1

где dn k – бесконечно малое изменение числа молей k -го компонента теплоно-

подведенного к системе охлаждения от рабочих газов в неравновесном процессе равно количеству теплового потока, подведенного к системе в обратимом процессе без некомпенсированного теплово-

сителя за счет массообмена с внешней

средой.

С учетом уравнения Q/T=d е S +

d i S , определение теплоты для процессов

го потока на процессы диссипации, и соответствует тепловому потоку, отводимому теплоносителем из системы охлаждения, т.е.

тепломассообмена ОЖ с внешней средой бесконечно малого элемента объема (5)

может быть представлено в виде

ds ds      dh dp Ndc вн             ik

H

К d       d          d       dt k1

dqw  dq   diq dt dt dt

С учетом уравнения (11) опреде-

ление количество теплоты, отводимой от многокомпонентной открытой термодинамической макросистемы, можно представить в виде:

Производство энтропии, обусловленное только процессом теплопроводности в формуле (12), может быть приведено к виду:

ds_вн d N

dh dp

= p —T"

dd

• ••

Z ^ t

k 1

dck     dis

T • d        dt

— VT 1 —          1 —

J_a — = - J_a Vln T = - J_a^

q ₂ T q         T q

Отметим, что

s p , nk

. (13)

cpm температурная

Данное уравнение выражает количество теплоты, отводимой из открытой системы охлаждения в окружающую среду.

Возле стенки цилиндра потоки теплоносителя представляют собой двухфазную систему, концентрация в жидкой фазе связана с концентрацией в паре условиями равновесия. И локальное производство энтропии в элементе объема неравновесной открытой термодинамической системы имеет следующий вид:

ds    1

G = P i^^-- J^g^OT + ...

dt     _T ²

часть удельной массовой энтропии определяется выражением:

s c lnT или s c      T T . (14)

pm            pm

Кроме того, будем иметь в виду

[4], что

^VH kT =^Pkp,T^+Vk -^P^

где V_k – парциальный молярный объем частиц k -го компонента.

Таким образом, уравнение (10) позволяет глубже заглянуть в сущность явления, происходящего в системе охлаждения двигателя. Из уравнения видно, что значение параметра зависит от интенсивности потоков и гидродинамики системы охлаждения.

• *“^—m ^tj Kk [ Kk  ^И к 1  •••

Tk

1     '                            ^— '

• - - -^pk ^{: Grad (1} - xk )" ^wk ~ -

  -—p"

  • ••          7 i

  T^k

  
  

  —

  : Gradx -w^ ^ 0 ,

  
  

  Литература