Термодинамический анализ трубопроводной системы отопления

Введение . Трубопроводные системы отопления связаны с проблемой коррекции динамических свойств, сокращения потерь тепловой энергии, а также совершенствования режимов передачи энергии теплоносителя. На тепловой баланс трубы системы отопления с постоянной по длине температурой греющего агента в большинстве случаев влияет изменение скорости потока [1–3]. Для успешного решения проблемы сбережения энергетических ресурсов необходимо совершенствование методов расчета, позволяющих выбирать наиболее рациональные проектные решения

Цель работы. Исследование теплового баланса трубы системы отопления с постоянной по длине температурой греющего агента.

Объекты и методы исследования . Объектом исследований выбрана трубопроводная система отопления. На рисунке 1 приведена расчетная схема теплового баланса трубы системы отопления с постоянной по длине температурой греющего агента.

Допущения:

• 1.    Свойства обрабатываемого теплового потока неизменны во времени и по длине аппарата.

• 2.    Температура стенки берется как среднеинтегральная по толщине.

• 3.    Тепловой поток в аксиальном направлении пренебрежимо мал.

• 4.    Коэффициенты теплоотдачи постоянны по длине аппарата.

Для исследования выделим на расстоянии х от входа обрабатываемого потока элемент dx (рис. 1).

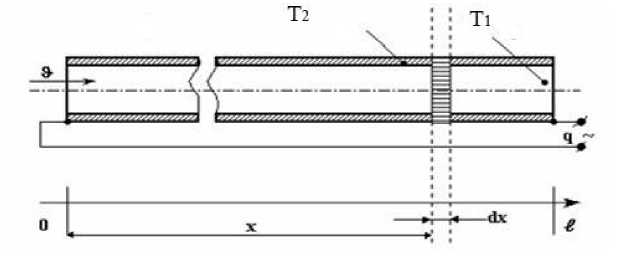
Рис. 1. Расчетная схема теплообменника

Принятые обозначения: x – текущая координата теплообменника, м; l – длина теплообменника, м; t – текущее время, с; D,d – диаметр трубы, м; с – теплоемкость; γ – плотность теплоносителя; α – коэффициент теплоотдачи, &- скорость движения; &0 – постоянная начальная скорость; δ & – возмущение скорости; T 1 – температура теплоносителя; T 2 – температура поверхности трубы; q – удельный тепловой поток; k – коэффициент; f, ψ – возмущающие функции θ, f, δ & – преобразование Лапласа по переменной t соответственно для θ, f , δ &; δθ – отклонение температуры от номинального значения вследствие изменения скорости δ &.

Дифференциальный тепловой баланс для элементарного кольца стенки за время dt

л ( D ² -d ² )

C2X2    ~ dx • dT2 = а12 ( T1 - Т2)∙^d ∙ԁх∙dt+ a32nD∙dx∙(Т3 -Т2)∙dt.(1)

Так как поток движется, то полная производная     будет равна

• dTi _ dTi ■

dt     dt + ftdx         .(2)

Преобразовав (1), (2), получим систему двух дифференциальных уравнений в частных производных с краевыми и начальными условиями

£7 1 ₊ ■ft — . J₍ T dt ^{+ ft}i x T ₁₂ ⁽ T ²

-

T i ) ;

У ^dt = A (T Л _dt T 21 ⁽¹¹

-

^ 2 )+к■q ;

T 1 ( х ,0)= ^ 2 ( х ,0)=0; T 1 (0, t )= / 1 ( t); ^ 21 ‘ к■q ( t)=* 3 ( t)․

Здесь / 1 (t), / 3 (t) и ^₃ (t) – произвольные функции времени.

На температуру T 1 трубы системы отопления с постоянной по длине температурой греющего агента влияет изменение скорости потока. При скорости потока ^ 0 начальная температура составляет соответственно T 10 и T 20 . При изменении скорости ^ 0 + 8ft (t) можно записать уравнение (3) в виде

d ( T ₁₀ +∆ T ₁ )

⁽ ft o + 3ft ) — -^— ¹⁾ + dx

d ( ^T 10 +∆ T 1 ) dt

^{=   (T} 20 +∆T 2

^T 12

^{- T} 10 -∆T 1);

d ^(T 20 +∆T 2 )1 T

----К ----= T-( ^T3

-

^T 20 -∆T 2 )+   ( ^T 10 +∆T 1 ^{- T} 20 -∆T 2 )․

^T 21

Пренебрегая членами второго порядка малости, систему запишем в виде двух систем дифференциальных уравнений:

• 1)    исходная (невозмущенная)

i 3710 + £По +

=(По ^- ^10);

7 12

дТ₂₀ 11

=   ( Тз - Т2о)+   (По - По); ut Из          П1

По( х ,0)=По( х ,0)=0; По (0, t )=л( t ); Тз =  ( t )․

• 2)    система в отклонениях

д ∆ и   д ∆ Т1

+

-∆И)- 81 ∙

£По.

;

д_ ∆ 11 dt

д ∆ Т₂    1

^-      ₊   (∆ Ъ -∆ Т₂ );

J23    *21

∆И( х ,0)=∆ т₂ ( х ,0)=0; ∆ Ti (0, t )=∆ т₂ (0, t )=0․

Приращение температуры ∆Т1 запишется в виде уравнения аПо (р, * )       -exp(- ∙1) f                                  (7)

| →0=          ∙т (    -    )․

Операторное уравнение температуры ∆Т1 запишется лт( X    s^ (V)    - л 1 N(V)-х 1--х м(V)

∆ ( , )==     ₍ fio -   ) ∙(р₎ ⁾ *exp(-й₀ ∙ )-exp(-∙ (р ₎)+

.

На рисунке 2 представлена схема моделирования передаточной функции по изменению скорости потока. Особенностью этой схемы является необходимость тщательной установки коэффициента exp (- ∙ ) так, чтобы он в точности был равен коэффициенту усиления звена exp (- ∙ ^{( )} ) в статике.

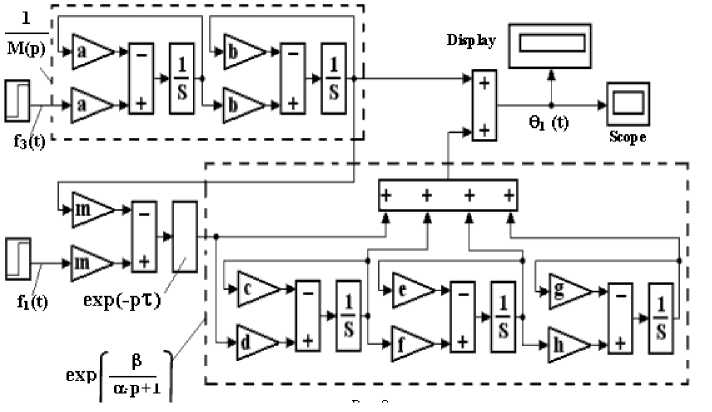
Рис. 2. Схема моделирования передаточной функции по изменению скорости потока

С учетом изменения коэффициента теплоотдачи при изменении скорости операторное уравнение температуры ∆ T_x будет идентичным

∆ F ( P , x )

__™ ( P ) _{(   -   )} 0,2∙ Nr ( P )

==     (  -   ⁾      - 7

^0                P ^∙ Q ( P )

exp(- ∙ ¹ )-exp(-   ^∙ £ ( ⁽ : ₎ ⁾ )+․

При выводе математических моделей были приняты следующие обозначения: Постоянные времени

T ₌   ^∙ n ^∙ ^ ; T ₌   ^{∙ 712} ∙( _D^ ) _; T ₌   ^∙ 1-Z ∙(      ) _; T =     ( t₂₃ +1) .

• ¹²     4∙^a21 ;      =      ∙ ^21 ∙ a ;      =     ∙ ^a32 ∙ d ;   =     (    +1) .

Многочлены от р

M ( P )= T12T23P² +( T + ^23) P +1 ; N ( P )= T12T23P + T ;

N_± ( P )= N ( P )+4~_T ^∙ 123 ;   ( P )=П₂^∙ ^23 ^∙ T ( p +   +   + г- ^- 7 ) ․

¹21                                   ^v *12    *21    *23    *

Результаты моделирования приведены на рисунках 3 и 4. На рисунке 3 приведены зависимости изменения температуры при скачкообразном возмущении скорости потока.

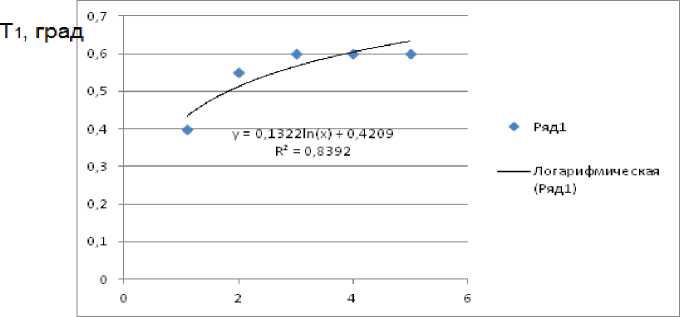
Рис. 3. Изменение температуры при скачкообразном возмущении скорости потока

На рисунке 4 приведены результаты моделирования при ступенчатом изменении скорости потока.

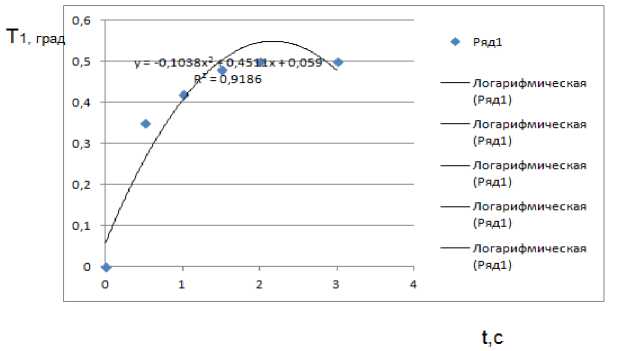
Рис. 4. Изменение температуры при ступенчатом изменении скорости потока

Статистическая ошибка составила exp(0,5) - (1 + 0,5 + 0,125 + 0,02) = 0,003, что допустимо.

Заключение

• 1.    Математическая модель трубопроводной системы отопления позволяет моделировать переходные процессы, связанные с изменением режима истечения теплоносителя.

• 2.    Результаты моделирования динамических процессов трубопроводной системы отопления позволили установить влияние скорости потока на недогрев теплоносителя и компенсацию за счет увеличения коэффициента теплоотдачи.