Термодинамический стимул мартенситного превращения в сплавах Fe-C

Мартенситное превращение (МП) лежит в основе важного для практики явления закалки сталей. Главная особенность МП заключается в том, что оно происходит при невысоких температурах и быстром охлаждении, так что атомы углерода не успевают выделиться из материнской фазы – аустенита в виде частиц карбида. В силу этого превращение в α -фазу происходит без участия диффузии углерода, поэтому уравнения химического равновесия, при этом переходе выполняться не могут. Мартенситный переход напоминает полиморфное превращение в чистых металлах, т. е. условием метастабильного равновесия фаз является равенство свободных энергий аустенита и мартенсита. Для стали данного состава существует единственная температура T 0 , при которой выполняется данное условие [1, 2].

В отличие от T0, реальная температура начала мартенситного перехода Ms может быть легко измерена магнитными, дилатометрическими и другими методами. Казалось бы, если немного переохладить аустенит относительно точки T0, то, согласно законам термодинамики, должно начаться образование мартенситной фазы. В действительности для начала МП требуется значительное переохлаждение γ-фазы ниже T0 [1]. Например, для чистого железа [3], у которого T0=911, а Ms =540 °C, требуется переохлаждение на 370 градусов. Дело в том [1], что для образования мартенситных кристаллов необходимо дополнительное расходование свободной энергии γ-фазы на упругую и пластическую деформации, поверхностную энергию мартенситных пластин и образование дислокаций и микродвойников в них. Единственный источник этой работы есть разность свободных энергий исходной и конечной фазы. К моменту начала МП величина разности Gα - Gγ достигает критического значения ΔGsγ→α , которую в металлофизике называют движущей силой, или термодинамическим стимулом мартенситного превращения [1, 2]. Концентрационная зависимость стимула показывает влияние углерода на меру упругой и поверхностной энергии в кристаллах мартенсита. Проблема заключается в том, что его невозможно определить экспериментальным путем. Цель настоящей статьи состоит в исследовании термодинамического стимула МП как функции содержания углерода в стали на основе термодинамического анализа. Отличие данной работы от предыдущего исследования [3], проведенного при участии одного из соавторов, заключается в следующем. В работе [3], следуя [4, 5], было использовано значение параметра деформационного взаимодействия λ0 = 2,73 эВ/атом. Однако недавние работы по компьютерному моделированию z-упорядочения углерода [6] дали иной результат: λ0 = 5,5 эВ/атом, причем в литературе имеются и более высокие значения [7, 8]. Во-вторых, в [3] не был учтен важный критерий устойчивости упорядочения: η > 0,5.

Методика термодинамических расчетов

По аналогии с работами [3, 9, 10], разделим реакцию бездиффузионного образования тетрагонального α-мартенсита из матричной ГЦК-фазы на два этапа: 1) образование объемно-центрированной кубической фазы, у которой ближний порядок в расположении атомов углерода унаследован от аустенита, и 2) образование тетрагонального мартенсита путем упорядочения атомов углерода в порах одного типа.

Соответственно изменение свободной энергии при у^а' -превращении можно записать в виде суммы:

A G ^Y ^"' =A G ^y^" +A G “^“' , (1)

E C - C = z ^S C - C

1 -

^{1 - 2} y c ^{(1 -} 8 ) [ y c ^{( 1 -} y c ) ]

^{( 1 - 2} f ^{5)( 1 -} y c ^- f ⁾⁽ y c ^- f )

Здесь e _C-C - энергия взаимодействия соседних атомов углерода (в расчете на моль), а f и δ – параметры ближнего упорядочения:

5 = ^{1 -} exp l ^-

^£ C - C Y RT ^J ;

f = ¹ -[ 1 ^{- 4 5( 1 -} y C ) y C ]

где A G ^Y ^“ - изменение свободной энергии при бездиффузионном образовании ОЦК-фазы (пересыщенного феррита) из ГЦК-фазы (аустенита); A g ^а ^“ — изменение свободной энергии при превращении кубической α-фазы в тетрагональную (α′).

Если активности углерода в γ-растворах из-

вестны, то можно записать выражение для моляр-

ной свободной энергии [10]:

G ^Y = ° G Fe ( 1 - x _C ) + x _C RT ln a C t + + ( 1 - x _C ) RT In a Fe +°ф С x _C.

Аналогичное выражение справедливо для α-раст-воров. Поэтому легко видеть, что

A G " = ( 1 - x c ) A° G + ( 1 - x c ) ln

а a"

aY

V a Fe I

+

Г „а 1

+ x_c RT ln

— + А°ф^^а x c,

а Y

V a C I

x y=i—.

^{1 - x} C

Согласно [3], энергия отталкивания e _C-C ближайших атомов углерода в Y -фазе составляет 7,7 кДж/моль, а энергия притяжения ближайших атомов a-фазы е "_{- С} = - 33 кДж/моль. Последовательно применяя принцип наследования, при расчете E "- с значения параметров ближнего порядка принимали такими же, как для аустенита ( z a = 8, z ^Y = 12).

Для оценок A°ф C ^^a использованы данные наиболее авторитетных экспериментальных исследований по измерению активности углерода в феррите и аустените [3]. По этим данным (в кДж/моль),

105,44 - 0,0453 T , T > 1026 К;

112,13 - 0,0514 T ; T < 1000 К;       (5)

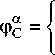
°Ф С = 44,02 - 0,0176 T ,

где A° G /. С" = ° G ^а - G ^Y и А°ф C ^“ - изменение

откуда

при Y^ a-переходе величины потенциалов в стандартных состояниях компонентов, в качестве которых для атомов железа принимают чистое Y — или α-железо, а для атомов углерода – бесконечно разбавленные Y — и а -твердые растворы, где a " _e, a Fe ,

а aC, a'C - активности железа и углерода в этих

a°t C ^" =

+ 68,11 - 0,0338 T , T < 1000 К;

+ 61,42 - 0,0277 T , T > 1026 К.

Наконец, отметим, что для разностей свободных энергий a- и Y -фаз чистого железа были использованы данные [11] (в Дж/моль):

A° G ^^а =° G ^Y-° G ^а =- 1462,4 + 8,282 T -

растворах, x _C – атомная доля углерода в растворе (химический состав y - и а -фаз одинаков).

Для описания активностей, следуя работе [3], используем предположение о бездиффузионном характере образования мартенсита, в силу которого энтропия смешения в ходе превращения не изменяется. Тогда, как показано в [3], в квазихими-ческом приближении уравнение (6) может быть записано в виде:

A G = A ° G V" ( 1 - x _C ) + x _C А°ф^ “ +

⁺ 2^⁽ E ~ "  E C—c ) •           (4)

где E C–C есть усредненная энергия взаимодействия атомов углерода в α- или γ-растворах:

- 1,15 T In T + 0,00064 T ² + G m (T ),          (7)

где G_m ( T ) – магнитный вклад в свободную энергию ОЦК-фазы, который имеет следующий вид ( т = T /1043):

G_m (T ) = _e

• - 9180,5 + 9,723 T -

• Г т4 т10 т161

• - 9309,8 — +---+--- для т< 1;   (8)

l 6   135 600 J

Гт - ⁴ т - ¹⁴    т - ²⁴ 1

- 6507,7 ---+--+--для т >  1.

I 10   315 1500 I

Учет тетрагональности . В теории Зинера – Хачатуряна [4, 5] возникновение тетрагонального

мартенсита в сталях рассматривается как неодинаковое заполнение атомами углерода трех подре-

Физическая химия и физика металлургических систем

шеток октаэдрических пор ( x , y и z ) из которых состоит решетка внедрения ОЦК-железа. Октаэдры атомов Fe не являются правильными, одна из пространственных диагоналей имеет меньший размер, чем две остальные. Для пор, отмеченных подрешеток, короткие диагонали направлены, соответственно, вдоль кристаллографических осей Ox , Oy и Oz . Количество пор в каждой подрешетке равно числу атомов железа N .

Когда атом углерода заполняет, например, пору z , он раздвигает расположенные вдоль короткой диагонали атомы железа, создавая локальное увеличение параметра решетки вдоль Oz , и тем самым стимулирует дальнейшее заполнение атомами углерода этой подрешетки.

Согласно теории Зинера [4] и Хачатуряна [5], свободная энергия упорядочивающейся в z -подрешетке системы атомов углерода при заданной температуре и концентрации углерода имеет вид:

A G "'" ' F ( c , T , n ) - F ( c , T ,0 ) =

• 1           kTn

• = - 3 Nc X0n + —3-^ x

• x[2 (1 -n) In (1 -n) + (1- 2n)ln (1- N],    (9)

• 3 np np

где n =------- есть параметр порядка, отра-

2nC жающий избыток атомов углерода в z-октаэдрических порах по сравнению с тем количеством, которое должно быть в при равномерном заполнении атомами углерода пор типа z, x, и y

(nC = nC = nC = —). Здесь N и nC - числа атомов железа и углерода соответственно; концентрация углерода с есть отношение этих чисел nx c = — =----, Ao — параметр деформационного

N 1 - xC взаимодействия атомов углерода, T – абсолютная температура, k – постоянная Больцмана; F(c, T,η) и F(c, T,0) – свободные энергии атомов углерода в упорядоченном и неупорядоченном (n = 0) состояниях.

Используя условие экстремума для свободной энергии, приходим к уравнению равновесия, которое определяет температурную и концентрационную зависимость параметра порядка η:

kT

Х о c

n

ln

Г 1 + 2 n v 1 -n

Нас, разумеется, интересует минимум A G “^“

.

Он достигается, если величина безразмерной тем-kT пературы ---< 0,36. Для этой области устойчи во c вого упорядочения 0,5 < n ^ 1. Изменения параметра дальнего порядка могут быть определены для произвольных значений температуры и концентрации по соотношению (10).

Результаты термодинамического моделирования

Результаты расчетов по формулам (1)–(10) зависимости разности свободных энергий γ- и α-фаз для сталей разного состава от температуры приведены на рис. 1. Точки начала мартенситного превращения нанесены на полученные зависимости в соответствии с экспериментальными данными, полученными в работе [12], что позволило рассчитать термодинамический стимул превращения, как расстояние от точек M_s до нулевого уровня изменения свободной энергии. Полученная концентрационная зависимость движущей силы мартенситного превращения приведена на рис. 2 и является основным результатом нашего исследования.

Видно, что зависимость является немонотонной и обладает выраженным максимумом в области концентраций углерода порядка 3 ат. %. В работе Коэна [9] было показано, что термодинамический стимул превращения составляет 1250 Дж/моль и не зависит от содержания углерода. Этот результат может показаться странным, поскольку понижение мартенситной точки, вызываемое добавлением углерода, приводит к возрастанию модуля упругости и плотности дислокаций, что должно увеличивать энергию образования мартенсита. В работе [3] наблюдали, что до 0,8 мас. % стимул постоянен, а затем он начинает снижаться. В нашем исследовании, этот результат подтвержден, но обнаружено, что в области малых концентраций стимул сначала возрастает, и только затем начинает снижаться. Особенность двух последних работ состоит в том, что был проведен учет дополнительной энергии деформационного взаимодействия атомов углерода, возникающий в тетрагональном мартенсите. Но в работе [3] для λ 0 было принято рекомендованное Хачатуряном значение 2,73, а в настоящей работе – более высокое значение 5,5 эВ/атом. Вероятно, начальное возрастание стимула связано с ростом затрат на образование полей напряжения и дислокаций в мартенсите, тогда как последующее снижение можно рассматривать как результат усиливающегося с ростом концентрации углерода деформационного взаимодействия атомов углерода в а’ -фазе, так как эта энергия пропорциональна квадрату концентрации. К этому следует добавить также, что модуль упругости закаленной стали снижается с ростом содержания углерода. Следовательно, будет уменьшаться и величина энергии, запасенной дислокациями, границами мартенситных пластин и двойников.

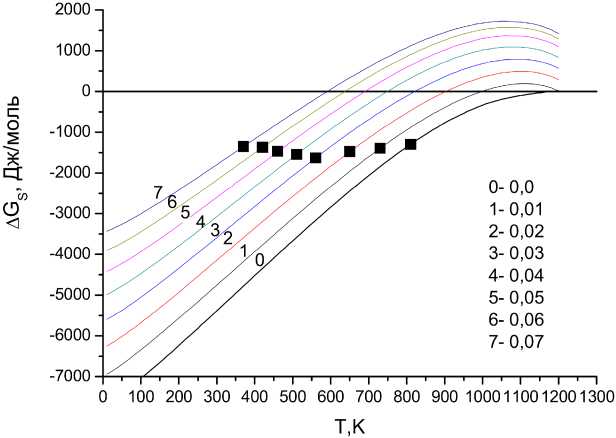
Рис. 1. Зависимость разности свободной энергии мартенсита и аустенита от температуры для различных значений концентрации углерода x _C (атомные доли). Черные квадраты – точки начала мартенситного превращения M_s [12]

1800-

600-

1600-

1400-

1200-

1000-

800-

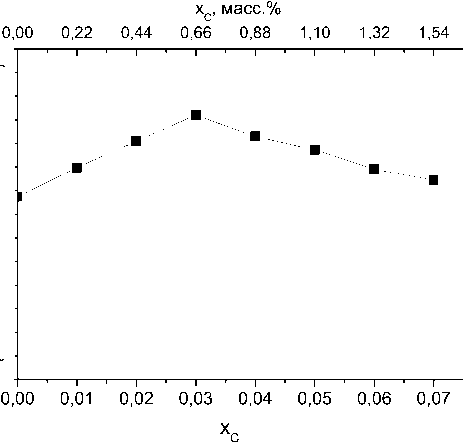
Рис. 2. Зависимость термодинамического стимула МП от содержания углерода в стали (внизу x _C в атомных долях, вверху – в мас. %)

Заключение

Таким образом, проведено изучение зависимости стимула образования мартенсита от концентрации углерода в стали с использованием новых данных для энергии деформационного взаимодействия и термодинамических характеристик ОЦК и ГЦК-железа. Показано, что стимул образования увеличивается с ростом содержания углерода до 3 ат. % (0,66 мас. %), а затем начинает заметно уменьшаться. Предположительно это связано с началом образования тетрагональной решетки мартенсита.

Настоящая работа поддержана грантом Российского научного фонда №16-19-10252.