Термодинамическое моделирование фазовой диаграммы системы Cu2O-BaO-Fe2O3

Гексаферрит бария представляет интерес как материал с ферромагнитными свойствами с возможностью использования в СВЧ устройствах [1–4]. Известно, что ионы железа в кристаллической решетке BaFe 12 O 19 могут быть частично заменены ионами других металлов, что может значительно повлиять на свойства гексаферрита [5–10]. В частности, возможно частичное замещение ионов железа ионами меди [10], что значительно повышает интерес к системе Cu 2 O–BaO–Fe 2 O 3 . Следует отметить, что в литературе отсутствуют сведения по фазовой диаграмме данной системы.

Целью настоящей работы является термодинамическое моделирование поверхности ликвидуса диаграммы состояния системы Cu 2 O–BaO–Fe 2 O 3 .

Подробно методика моделирования диаграмм состояния оксидных систем приведена в работах [11–15]. Для расчета координат поверхности ликвидуса фазовой диаграммы тройной системы необходимо провести расчет координат линий ликвидуса диаграмм состояния двойных систем, входящих в состав исследуемой системы. Следовательно, в рамках настоящей работы в первую очередь необходимо провести термодинамическое моделирование линий ликвидуса диаграмм состояния систем Cu 2 O–BaO, Cu 2 O–Fe 2 O 3 , BaO–Fe 2 O 3 , а затем, опираясь на полученные данные, рассчитать координаты поверхности ликвидуса фазовой диаграммы тройной системы Cu 2 O–BaO–Fe 2 O 3 .

Методика применяемого в данной работе расчета опирается на координаты (состав и температура) наиболее надежно определенных характерных точек на диаграммах: точек эвтектических, перитектических, фазовых переходов (например, плавления веществ в исследуемой системе) и т. п. Таким образом, для моделирования диаграмм состояния необходимы сведения о температурах и энтальпиях плавления веществ исследуемой системы. В табл. 1 приведены данные для веществ, входящих в систему Cu2O–BaO–Fe2O3.

Для моделирования линии ликвидуса диаграммы состояния системы Cu₂O–Fe₂O₃ использовалось приближение теории совершенных ионных растворов [11]. Расчет координат линий ликвидуса систем Cu₂O–BaO, BaO–Fe 2 O 3 , а также координат поверхности ликвидуса системы Cu 2 O–BaO–Fe 2 O 3 проводился с использованием приближения теории субрегулярных ионных растворов [11]. При проведении моделирования оксиду меди Cu 2 O был присвоен индекс «1», оксиду бария BaO – индекс «2», а оксиду железа Fe 2 O 3 – индекс «3». Все расчеты производились для парциального давления кислорода, равного 10 Па (10^–4 атм) в каждой из исследуемых систем.

Значения энергетических параметров модели субрегулярных ионных растворов для двойных оксидных систем определялись в процессе решения систем нелинейных уравнений, для чего использовался метод Ньютона. Для составления уравнений использова- лись данные о составах ряда опорных точек, выбранных на линии ликвидуса фазовых диаграмм. Для каждого набора данных составлялось выражение, связывающее данные о равновесных составах при данной температуре с параметрами модели.

Для моделирования тройной оксидной системы необходимы также сведения о перекрестных энергетических параметрах взаимодействия теории субрегулярных ионных растворов, формула для расчета которых приведена в работе [13].

Энергетические параметры теории субрегулярных ионных растворов, использованные в данной работе при проведении термодинамического моделирования, приведены в табл. 2.

Сведений о виде диаграммы состояния системы Cu 2 O–BaO в литературе не имеется, однако есть данные о наличии соединения BaCu 2 O 2 , а также о том, что характер плавления этого соединения – конгруэнтный, а его температура плавления равняется 1015 °С [20]. Также согласно экспериментальным данным авторов работы [20] в системе имеются две точки эвтектики: при температуре 940 °С оксидный расплав находится в равновесии с Cu 2 O и BaCu 2 O 2 ; при температуре 890 °С оксидный расплав находится в равновесии с BaO и BaCu 2 O 2 . Результаты проведенного в ходе выполнения данной работы термодинамического моделирования линии ликвидуса

Таблица 1

Данные о температурах и энтальпиях плавления веществ, входящих в систему Cu 2 O–BaO–Fe 2 O 3

Вещество	Т 0 ОГ Tm , С	A m H 0 , Дж/моль T m
Cu 2 O	1242 [16]	64 300 [16]
BaO	1925 [17]	57 768 [18]
Fe 2 O 3	1539 [19]	87 000 [19]
BaCu 2 O 2	1015 [20]	97 310 [настоящая работа]
CuFeO 2	1197 [17]	64 350 [17]
Ba 3 Fe 2 O 6	1318 [настоящая работа]	240 300 [настоящая работа]
Ba 2 Fe 2 O 5	1358 [настоящая работа]	119 300 [настоящая работа]
BaFe 2 O 4	1358 [настоящая работа]	207 175 [настоящая работа]
BaFe12O19	1457 [настоящая работа]	424 265 [настоящая работа]

Таблица 2

Энергетические параметры ( Q ijkl ) теории субрегулярных ионных растворов, Дж/моль

Q1112 Q1122 Q1222 Q1113 Q1133 Q1333 –74 210 –91 549 –103 554 0 0 0 Q2223 Q2233 Q2333 Q1123 Q1223 Q1233 –68 319 –60 274 –29 169 –159 425 –247 784 –126 634 фазовой диаграммы системы Cu2O–BaO приведены на рис. 1.

Литературных экспериментальных данных о диаграмме состояния системы Cu2O– Fe2O3 в литературе также не приводится. Имеются сведения о наличии соединения CuFeO2 [17]. Несмотря на то, что приводятся данные о температуре плавления CuFeO2 (1197 °С), сведений о характере плавления соединения (конгруэнтный или инконгруэнт-ный) не имеется. Результаты термодинамического моделирования линии ликвидуса фа- зовой диаграммы системы Cu2O–Fe2O3 приведены на рис. 2. Согласно проведенному расчету наиболее термодинамически вероятен конгруэнтный характер плавления соединения CuFeO2.

Сведения о диаграмме состояния системы BaO–Fe 2 O 3 достаточно противоречивы [21–23]. Согласно экспериментальным данным Y. Goto и T. Takada [21] в системе присутствуют три соединения: Ba 2 Fe 2 O 5 , BaFe 2 O 4 , BaFe 12 O 19 , которые имеют конгруэнтный характер плавления. По экспериментальным данным H. Sato [22]

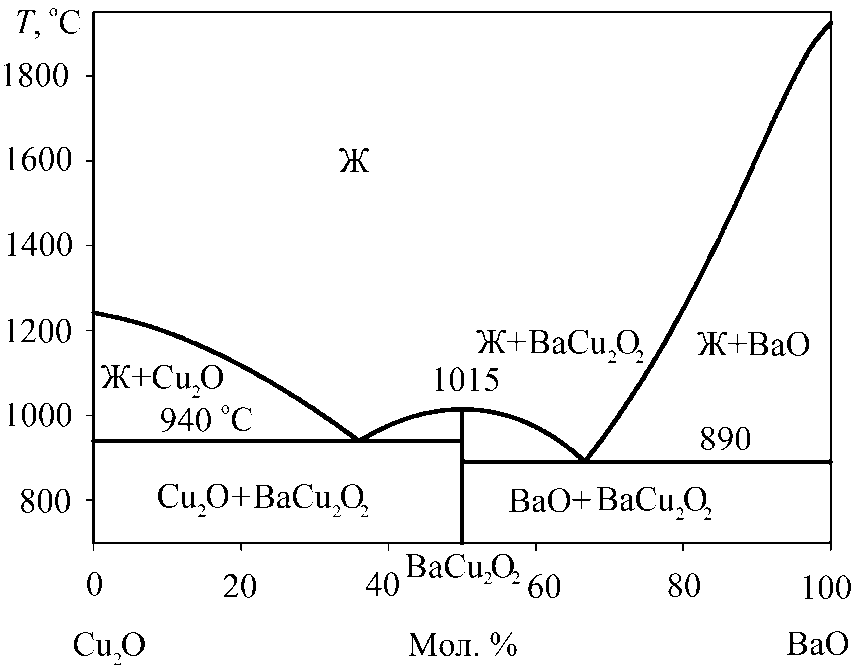
Рис. 1. Результаты расчета фазовой диаграммы системы Cu 2 O–BaO

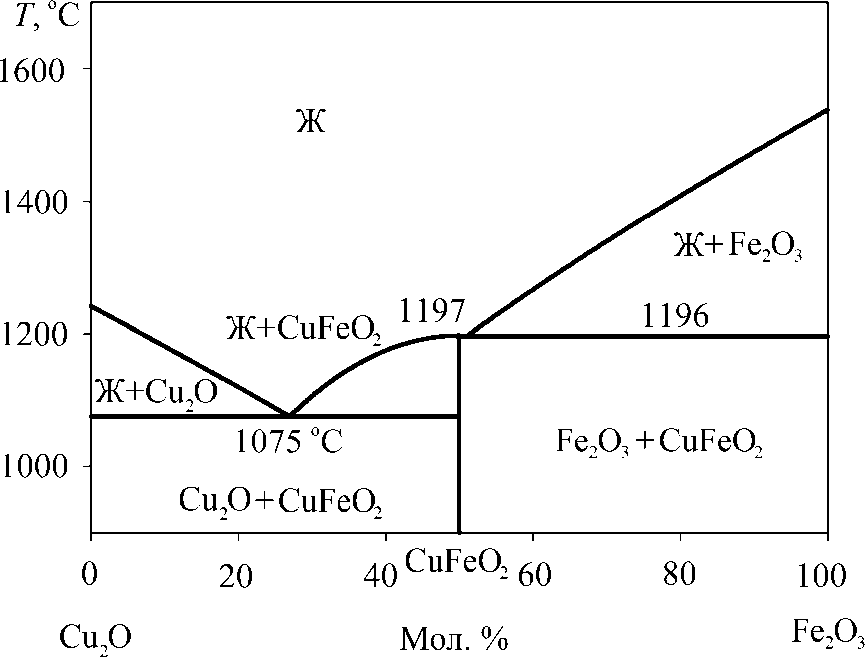
Рис. 2. Результаты расчета фазовой диаграммы системы Cu 2 O–Fe 2 O 3

в системе BaO–Fe2O3 имеются четыре соединения. Помимо ферритов бария, указанных в работе [21], в работе [22] приводится еще и соединение Ba3Fe2O6. Причем согласно [22] только Ba2Fe2O5 и BaFe2O4 имеют конгруэнтный характер плавления, соединения Ba3Fe2O6 и BaFe12O19 плавятся инконгруэнтно (по перитектическим реакциям). Д.А. Винник и др. в работе [23] приводят расчетную диаграмму состояния системы BaO–Fe2O3. Помимо четырех вышеуказанных ферритов бария, согласно [23] в системе имеется соединение Ba2Fe6O11, которое претерпевает твердофазный распад при температуре 1145 °С. Данные о положении линии ликвидуса исследуемой диаграммы состояния согласно литературным источникам [21–23] приведены на рис. 3 и в табл. 3.

Результаты проведенного в ходе выполнения данной работы термодинамического моделирования линии ликвидуса фазовой диаграммы системы BaO–Fe 2 O 3 также приведены на рис. 3 и в табл. 3.

Как следует из табл. 3 и рис. 3, в целом расчет, проведенный в ходе выполнения настоящей работы, достаточно хорошо совпадает с литературными данными. Наибольшее расхождение наблюдается для температуры плавления феррита бария BaFe 2 O 4 как между литературными источниками, так и между нашим расчетом и литературными данными.

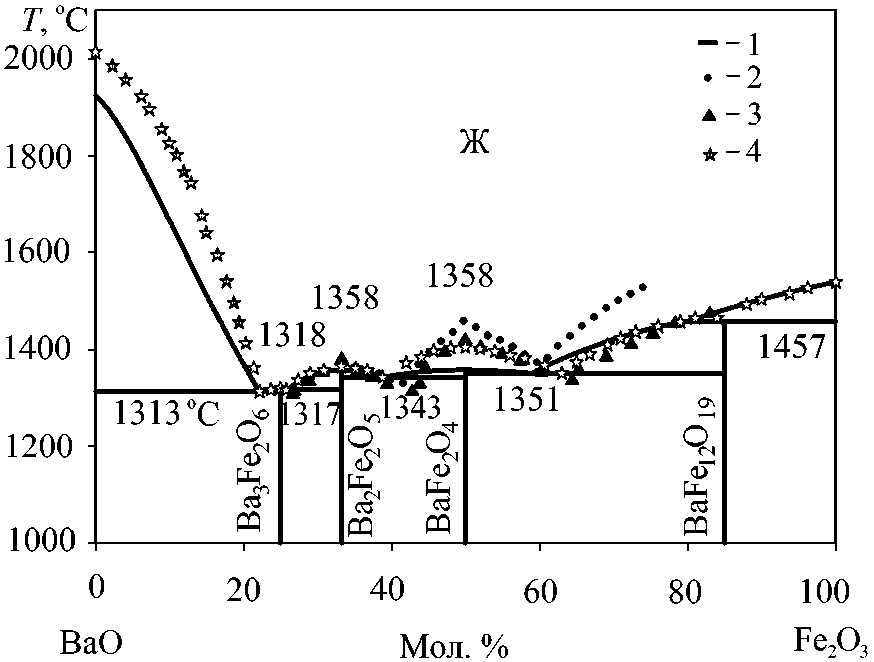
Рис. 3. Фазовая диаграмма системы BaO–Fe 2 O 3 : 1 – настоящая работа; 2 – экспериментальные данные [21]; 3 – экспериментальные данные [22];

4 – расчетные данные [23]

Таблица 3

Координаты характерных точек на диаграмме состояния системы BaO–Fe2O3

Вид фазового превращения	Состав, мол. %				Температура, °С
	[21]	[22]	[23]	Настоящая работа	[21]	[22]	[23]	Настоящая работа
Ж↔BaO+Ba 3 Fe 2 O 6	–	–	22,2	22,2	–	–	1313	1313
Ж↔Ba 3 Fe 2 O 6	–	–	25,0	25,0	–	–	1320	1318
Ж ↔ Ba 3 Fe 2 O 6 + Ba 2 Fe 2 O 5	–	26,7	25,8	25,9	–	1307	1317	1317
Ж↔Ba 2 Fe 2 O 5	33,3	33,3	33,3	33,3	1370	1380	1365	1358
Ж↔Ba 2 Fe 2 O 5 +BaFe 2 O 4	42,0	42,8	38,8	38,8	1330	1313	1343	1343
Ж↔BaFe 2 O 4	50,0	50,0	50,0	50,0	1460	1420	1405	1358
Ж↔BaFe 2 O 4 +BaFe 12 O 19	60,2	64,4	63,0	58,9	1370	1336	1351	1351
Ж+Fe 2 O 3 ↔BaFe 12 O 19	–	83,0	84,0	79,9	–	1474	1465	1457

Однак о в е ли чи н а рас хо жд е н и я н а хо д и тс я в п ред е л а х д оп у с ти мой п о гре ш н о с ти . Т ак, относительная погрешность δ д ля оп ре д е л е н н ой терм оди намическ им м о де л и ровани ем в на стоя ще й ра боте те мпе ра ту ры п ла в ле н и я BaFe₂O₄ п о отн ош ен ию к э к с п е ри ме н та л ьн ым данным [21] составляет 6,99 %; по отнош е н и ю к э к с п е ри ме н та л ьным д а н н ым [ 22 ] равняется 4,37 %; а п о от н о ш ени ю к рас че тным да н н ым [23] и м е е т в е ли ч и н у в 3, 35 %.

В ходе моделировани я ди а грамм с о с тоя н и я д в ой н ых сис те м бы ли оц е н е ны э н та л ь п и и , те мп е рат у ры и э нтроп и и п лавл е н и я со ед и н е н и й , об р а зующ и хся в э ти х с и с те ма х. Да н н ые п о те мпе ра ту ра м и э н та льп и ям п л ав л е н и я с ое д и не н и й п ри в ед е н ы в та бл. 1. Э н троп и и п лавл е н и я с ое ди н е н и й с лед у ю щ и е, Дж /( мо ль· К) : 26,12 (д ля сое д и н е н и я BaCu 2 O 2 );

20,76 (для соединения CuFeO 2 ); 90,12 (для соединения Ba 3 Fe 2 O 6 ); 25,91 (для соединения Ba 2 Fe 2 O 5 ); 97,25 (для соединения BaFe 2 O 4 ); 199,25 (для соединения BaFe 12 O 19 ).

В литературе отсутствуют сведения по фазовой диаграмме системы Cu 2 O–BaO– Fe₂O₃. Результаты выполненного в ходе настоящей работы расчета координат поверхности ликвидуса данной тройной оксидной системы приведены на рис. 4. На диаграмму нанесены изотермы с шагом в 100 °С в интервале температур от 900 до 1900 °С. Координаты точек нонвариантных превращений, реализующихся в системе, приведены в табл. 4. Следует отметить, что в тройной системе, согласно результатам моделирования, реализуется ряд равновесий, которых нет на двойных диаграммах состояния исследуемых систем.

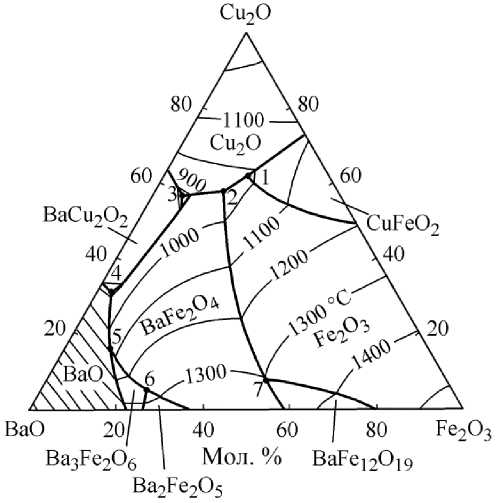
Рис. 4. Результаты моделирования полной проекции поверхности ликвидуса системы Cu 2 O–BaO–Fe 2 O 3 . Точки 1–7 – см. табл. 4

Таблица 4

Координаты точек нонвариантных превращений на диаграмме состояния системы Cu2O–BaO–Fe2O3

№ точки	Состав, мол. %			Температура, °С
	Cu 2 O	BaO	Fe 2 O 3
1	61,7	18,9	19,4	974
2	58,1	26,7	15,2	929
3	56,9	35,9	7,2	888
4	31,0	65,5	3,5	860
5	13,8	73,6	12,6	1108
6	4,1	70,9	25,0	1268
7	7,8	40,5	51,7	1306

Так, в частности, имеется равновесие оксидного расплава с моноферритом бария и с оксидом железа Fe 2 O 3 (линия «2–7»), которого нет в двойной системе BaO–Fe 2 O 3 .

Выводы

Проведено термодинамическое описание фазовых равновесий в системе Cu 2 O–BaO– Fe 2 O 3 . Определены термодинамические модели и их параметры, необходимые для описания фазовых диаграмм двойных систем Cu 2 O–BaO, Cu 2 O–Fe 2 O 3 , BaO–Fe 2 O 3 , а также поверхности ликвидуса тройной системы Cu 2 O–BaO–Fe 2 O 3 . В ходе моделирования оценены энтальпии, энтропии и температуры плавления соединений BaCu 2 O 2 , CuFeO 2 , Ba 3 Fe 2 O 6 , Ba 2 Fe 2 O 5 , BaFe 2 O 4 , BaFe 12 O 19 . Впервые определены координаты точек нонвариантных превращений в системе Cu 2 O–BaO–Fe 2 O 3 . Определены условия образования монокристаллов гексаферрита бария из оксидного расплава исследуемой тройной системы. При добавлении третьего компонента (оксида меди Cu 2 O) в систему BaO–Fe 2 O 3 температуры точек нонвариантных превращений с участием гексаферрита бария снижаются практически на 100 градусов до 1306 °С.

Работа осуществлена при финансовой поддержке РФФИ, грант № 16-08-00133 а.