Термодинамическое моделирование линии ликвидус системы Ni-Si

Интерес к системе Ni–Si обусловлен большим количеством образующихся в ней силицидов. Известно, что силициды никеля в сплавах системы Cu–Si–Ni существенно упрочняют их [1]. С другой стороны, одной из рекомендуемых [2] методик повышения эффективности удаления никеля из меди при окислительном рафинировании является использование кремния при раскислении меди (так называемое «силицирование»). В работе [3] содержатся данные о возможности отделения силицидов никеля при электрохимическом растворении медного анода. Указывается, что скорость растворения основного материала анода на 2,5–3 порядка больше скорости растворения силицидных фаз.

Ключевой для понимания процессов, реализующихся в системе Cu–Si–Ni, является система Ni–Si, адекватная термодинамическая модель которой откроет путь к моделированию более сложных систем.

Методика исследования

Для моделирования фазовых равновесий, реализующихся в системе Ni–Si, опробовано два подхода: посредством модели регулярных растворов и с помощью модели субрегулярных растворов.

Активность компонентов бинарной системы в приближении теории регулярных растворов описывается выражением [4]:

(1-Ni )2 Q ai = Nie RT .                                                                                      (1)

В соответствии с приближением теории субрегулярных растворов [5] активность компонентов для бинарной системы будет равна

Nj ²( NiQj + NjQji )

a i = N i e      RT .                                                                                (2)

В этих формулах N – атомные доли компонентов раствора; Q – энергии смешения его компонентов; Т – температура; R – универсальная газовая постоянная.

Методика моделирования состоит в следующем. На первом этапе расчета определяются значения энергий смешения Q . Для этого используются данные по температурам и теплотам плавления чистых простых веществ, а также литературные данные о положении некоторых (реперных) точек на линии ликвидус диаграммы состояния. Далее, зная параметры Q и задаваясь значением атомной доли компонентов раствора, рассчитывается вся линия ликвидус для выбранной системы. Следует отметить, что для систем с интерметаллидами, силицидами и т. п. на стадии определения Q требуются данные по константам плавления соединений. Если литературных данных нет, то методика расчета позволяет их оценить.

Согласно диаграмме состояния системы Ni–Si [6] в ходе взаимодействия никеля с кремнием могут образовываться следующие соединения: Ni 3 Si, Ni 5 Si 2 , Ni 2 Si, Ni 3 Si 2 , NiSi и NiSi 2 . В некоторых источниках указывается на существование еще и фаз Ni 31 Si 12 и Ni 25 Si 9 [7, 8] (рис. 1).

Физическая химия

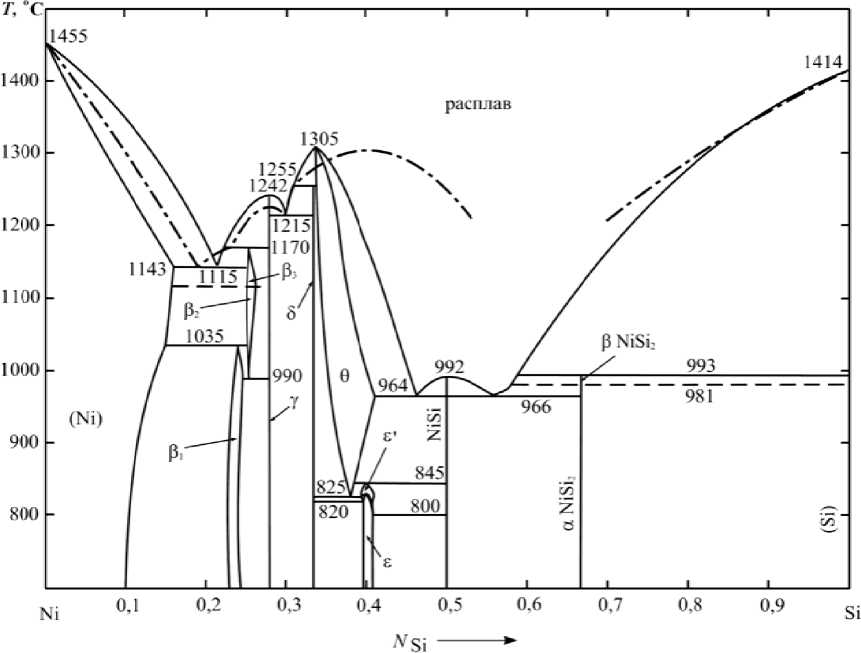
Рис. 1. Диаграмма состояния системы Ni–Si: сплошные линии – литературная диаграмма [8]; пунктир – результат расчета по теории регулярных растворов

Данная диаграмма состояния характеризуется большим количеством двойных соед и нений.

Процесс перехода соединения в жидкое состояние будем описывать сле д ующей реакцией:

|MmNn| = m[M] + n[N].(3)

Здесь |M m N n | – чистое твердое соединение; [М] и [N] – компоненты металли ч еского расплава.

Для реакции (3) закон действующих масс (актив н ость соединения равна 1)

K = «[M]«[N].

Если температурную зависимость константы рав н овесия реакции (3) записать в виде

1g K = -T + B,(5)

то с учетом соотношений (4), (5) можно получить

A m lg «[M] + n lg «[N] + T " B = 0.

Используя выбранные опорные точки диаграммы, а также значения т еплот плавления для никеля и кремния, можно определить значения энергий смешения компон е нтов расплава системы Ni–Si, а также величины A и B для реакций образования из компонентов расплава с илицидов этой системы.

Термодинамические характеристики плавления чистых веществ приведены в табл. 1.

Таблица 1

Температуры и теплоты плавления веществ по данным справочника [9]

Вещество	o T m , С	A m H O0 , Дж/моль Tm
Si	1414	49789
Ni	1455	17489

Обсуждение результатов

Помимо литературных данных, обобщенных в с п равочнике [8], на ри с . 1 приведена диаграмма состояния, рассчитанная по теории регулярных растворов. Значение энергетического параметра, использованное в ходе расчета, Q = –18741 Дж/моль. Расчет по теории регуляр н ых растворов недостаточно корректно описывает линию ли к видус, а для некоторого интервала значений атомной доли кремния полученные данные не имеют физического смысла и на рис. 1 этот участок линии ликвидус не представлен.

На рис. 2 представлены результаты расчета по теории субрегулярных рас т воров. Полученные результаты вполне согласуются с литературной диаграммой состояния. Однако есть и ряд отличий расчетной диаграммы состояния от литературной. Прежде всего, в избранном нами приближении не учитывалась нестехиометричность состава некоторых силицидов. Допустимос т ь такого упрощения связана с тем, что нас, прежде всего, интересовало положение линии ликви д ус. Фаза Ni 2 Si на расчетной диаграмме конгруэнтно плавится п ри 1305 °С, в то время как по литературным данным это соединение распадается по перитектической реакции. Также пришлось сделать некоторые допущения при описании равновесия распл а ва с силицидом NiSi₂. При расчете учитывалась только одна из его кристаллографических модификаций. Полученны е в работе з начения энергетических параметров для теории субрегулярны х растворов приведены в табл. 2, 3. Константы, характеризующие процесс перехода вещества в жидкое состояние, приведены в табл. 4.

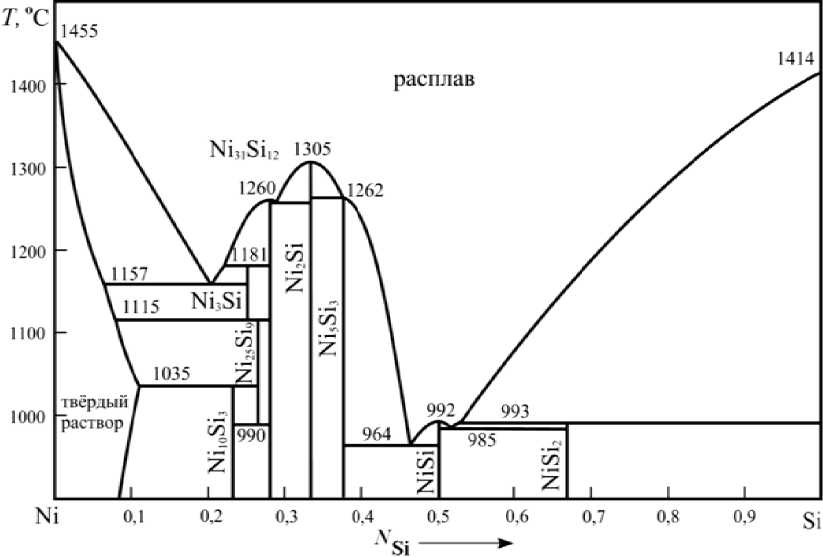
Рис. 2. Диаграмма состояния системы Ni–Si, рассчитанная в приближении теории субрегулярных растворов

Таблица 2

Параметры модели субрегулярного раствора для расплава (Дж/моль)

1                          2	Si	Ni
Si	0	–26269
Ni	–25970	0

Таблица 3

Параметры модели субрегулярного раствора для твёрдого раствора (Дж/моль)

1                          2	Si	Ni
Si	0	0
Ni	6000	0