Термодинамическое моделирование поверхности ликвидус диаграммы состояния системы Cu 2O-Al 2O 3-ZrO 2

Система Cu 2 O–Al 2 O 3 –ZrO 2 представляет интерес как часть сложной многокомпонентной шлаковой системы, образующейся при производстве алюминиевых и циркониевых бронз. Цирконий используется при плавке алюминиевых бронз как модификатор, улучшающий свойства медных сплавов (например, жаропрочность). А при производстве циркониевых бронз во избежание угара циркония металл предварительно хорошо раскисляют, например, алюминием [1]. Помимо этого исследование особенностей взаимодействия оксида меди с керамикой системы Al 2 O 3 –ZrO 2 актуально, так как такая керамика может использоваться в качестве огнеупора при производстве меди и сплавов на ее основе.

Для построения диаграммы состояния трехкомпонентной системы необходимы сведения и о диаграммах состояния бинарных систем. Поэтому целью данной работы стало проведение термодинамического моделирования линий ликвидус диаграмм состояния бинарных систем Cu₂O–Al₂O₃, Cu 2 O–ZrO 2 и Al 2 O 3 –ZrO 2 , а также моделирование поверхности ликвидус диаграммы состояния тройной системы Cu 2 O–Al 2 O 3 –ZrO 2 .

Подробно методика моделирования диаграмм состояния оксидных систем изложена в моногра- фии [2]. Расчет опирается на координаты (состав и температура) наиболее надежно определенных характерных точек на диаграммах: точек эвтектических, перитектических, фазовых переходов и т. п. Для моделирования диаграмм состояния также необходимы сведения о температурах и теплотах плавления чистых веществ. Для исследуемых систем эти данные приведены в табл. 1.

Координаты линий ликвидус диаграмм состояния бинарных систем Cu 2 O–Al 2 O 3 , Cu 2 O–ZrO 2 и Al 2 O 3 –ZrO 2 рассчитывались с помощью приближения теории субрегулярных ионных растворов, значения энергетических параметров теории приведены в табл. 2. Результаты моделирования представлены на рис. 1–3. Римскими цифрами на этих рисунках обозначены реперные точки, использованные при расчете.

Данных по диаграмме состояния системы Cu₂O–Al₂O₃ в литературе мало. В работе S.K. Misra и A.C.D. Chaklader [5] приводится лишь часть диаграммы состояния этой системы. Термодинамическое моделирование позволило описать линию ликвидус полностью (рис. 1). Помимо оксидов меди и алюминия в системе присутствует соединение CuAlO 2 . Использованная методика расчёта позволила оценить некоторые термодинамические

Физическая химия и физика металлургических систем

Таблица 1

Данные о температурах и теплотах плавления веществ

Вещество	Т 0 °C Tm , С	A mH ° , Дж/моль T m	Источник
Cu 2 O	1242	64 300	[3]
Al2O 3	2051	107 850	[4]
ZrO 2	2680	86 950	[4]

Таблица 2

Энергетические параметры теории субрегулярных ионных растворов

Система	Значения параметров
	Q 1112 , Дж/моль	Q 1122 , Дж/моль	Q 1222, Дж/моль
Cu 2 O–Al 2 O 3	+1050 ( Q 1112 )*	+42888 ( Q 1122 )*	+11313 ( Q 1222 )*
Cu 2 O–ZrO 2	–39940 ( Q 1113 )*	+18590 ( Q 1133 )*	–29628 ( Q 1333 )*
Al 2 O 3 –ZrO 2	+18407 ( Q 2223 )*	–7177 ( Q 2233 )*	+16812 ( Q 2333 )*

См. формулы (1)–(4).

Рис. 1. Диаграмма состояния системы Cu 2 O–Al 2 O 3 : сплошная линия – результаты моделирования по теории субрегулярных ионных растворов; штрихпунктир – литературные данные S.K. Misra и A.C.D. Chaklader [5]

Рис. 2. Диаграмма состояния системы Cu 2 O–ZrO 2 : сплошная линия – результаты моделирования по теории субрегулярных ионных растворов; литературные данные A.M.M. Gadalla и J. White [6] нанесены штрихпунктиром

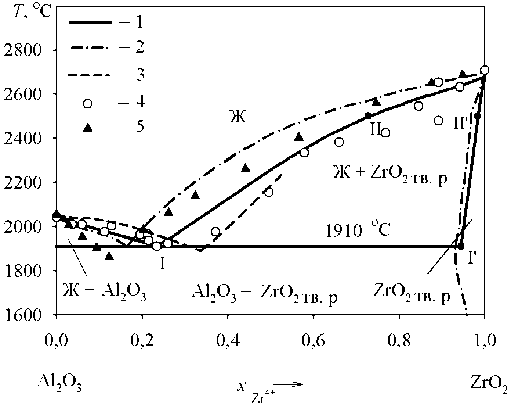
Рис. 3. Диаграмма состояния системы Al 2 O 3 –ZrO 2 : 1 –результаты моделирования по теории субрегулярных ионных растворов (линия ликвидус) и теории регулярных ионных растворов (твердый раствор на основе ZrO 2 );

2 – справочные данные А.С. Бережного [7]; 3 – экспериментальные данные H. Suzuki и др. [8]; 4 – экспериментальные данные G.R. Fischer и др. [9];

5 – расчетные данные W. Tao и J. Zhanpeng [10]

характеристики этого соединения: T m =1260 °С;

A H ° =106 544 Дж/моль; A S° =42,73 Дж/моль^К. mm mm

Сведения в литературе по диаграмме состояния системы Cu 2 O–ZrO 2 также немногочисленны. Координаты точки эвтектики для этой системы представлены в работе A.M.M. Gadalla и J. White [6]. Результаты термодинамического моделирования позволили построить линию ликвидус для всего возможного интервала составов (рис. 2).

Система Al 2 O 3 –ZrO 2 изучалась неоднократно [7–10]. Однако данные разных авторов по координатам точки эвтектики сильно расходятся (рис. 3). Координаты точки эвтектики меняются от 55 мас. % ZrO₂ и 1890 °С [8] до 25 мас. % ZrO₂ и 1862 °С [10]. За исходные данные для термодинамического моделирования были взяты данные [9] с координатами точки эвтектики 42,50 мас. % ZrO₂ и 1910 °С.

В процессе расчета диаграммы состояния системы Al 2 O 3 –ZrO 2 линия солидус, ограничивающая область существования твердого раствора на основе оксида циркония, была определена с использованием теории регулярных ионных растворов. Энергетический параметр теории, использованный при расчете, Q 12 = +58610 Дж/моль.

Для оценки адекватности проведенного термодинамического моделирования линий ликвидус были рассчитаны активности компонентов оксидного расплава для бинарных систем с оксидом меди. Результаты представлены на рис. 4–5. Расчеты проведены только для концентраций, при которых существует оксидный расплав. В рассмотренных интервалах a(Cu2O) , a(Al2O3) и a(ZrO2) характери- зуются отрицательными отклонениями от закона Рауля.

Данных по диаграмме состояния тройной системы Cu2O–Al2O3–ZrO2 в литературе нет. Расчёт поверхности ликвидус диаграммы состояния этой системы в настоящей работе осуществлялся с использованием теории субрегулярных ионных растворов на основании данных, полученных при моделировании бинарных систем.

Для построения поверхности ликвидус тройной диаграммы состояния необходимы сведения не только об энергетических параметрах, характеризующих бинарные системы, но и значения перекрестных энергетических параметров для тройной системы. Эти значения можно оценить по формулам:

SQ = Q ₁₁₁₂ + Q ₁₁₂₂ + Q ₁₂₂₂ + Q ₁₁₁ 3 + Q ₁₁ 33 +

+ Q1333 + Q2223 + Q2233 + Q2333;(1)

Q ₁₁₂₃ = ( SQ + 3 Q ₁₁₁₂ + Q ₁₁₂₂ – Q ₁₂₂₂ +

+ 3Q1113 + Q1133 – Q1333) / 4;(2)

Q ₁₂₂ 3 = ( SQ + 3 Q ₁₂₂₂ + Q ₁₁₂₂ – Q ₁₁₁₂ +

+ 3Q2223 + Q2233 – Q2333) / 4;(3)

Q ₁₂₃₃ = ( SQ + 3 Q ₁₃₃₃ + Q ₁₁₃₃ – Q ₁₁₁₃ +

+ 3 Q2333 + Q2233 – Q2223) / 4.(4)

Расчёт с использованием данных табл. 2 позволил получить следующие значения:

Q 1123 = –1141 Дж/моль;

Q ₁₂₂₃ = + 34831 Дж/моль;

Q ₁₂₃₃ = + 6703 Дж/моль.

Необходимые для моделирования сведения о константах равновесия перехода твердых веществ в жидкое состояние приведены в табл. 3. Для простых веществ расчет производился по формуле (5), а для соединения – по формуле (6):

Физическая химия и физика металлургических систем

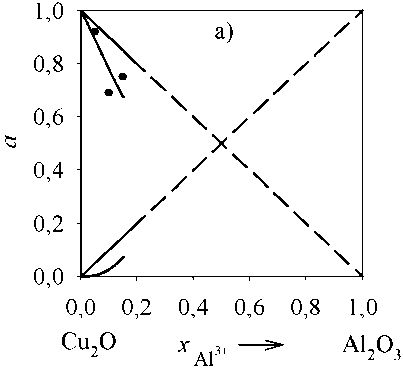
Рис. 4. Зависимость активностей компонентов оксидного расплава (Cu 2 O, Al 2 O 3 ) от состава: а) T = 1380 °С; б) T = 1500 °С; в) T = 2000 °С. Точками указаны литературные экспериментальные данные [11] при 1380 °С

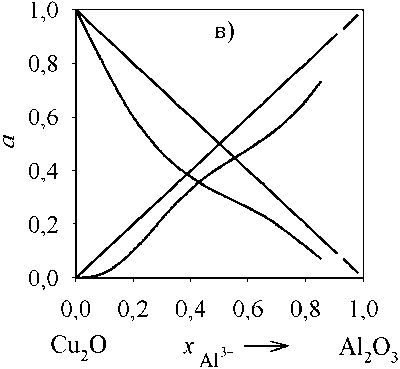
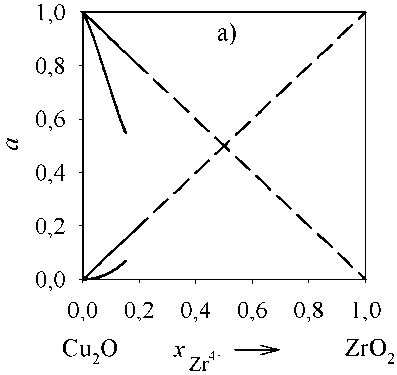
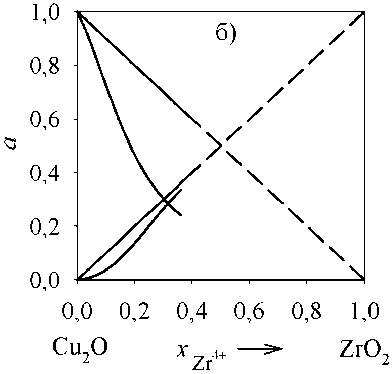
Рис. 5. Зависимость активностей компонентов оксидного расплава (Cu 2 O, ZrO 2 ) от состава: а) T = 1500 °С; б) T = 2000 °С

Таблица 3

Константы равновесия, характеризующие процесс перехода вещества в жидкое состояние

Вещество lgK Cu2O 3359 --+ 2,217 T Al2O3 5633 --+ 2,424 T ZrO2 - 4541 +1,538 T CuAlO2 (Cu2O·Al2O3) 5565 --+ 2,232 T lgKпл

A m H °_r    A m H °

_________ ¹ m + ¹ m ;

2,303 RT 2,30 3 RTm ’

lg K пл

A mH°_r ____________ ¹ m । 2,30 3 RT

A m S°_r

m

2 ,30 3 R

Здесь K _пл – к онс тан та ра вновесия п ерехода тверд ого вещества в жидкое состояние; A_m H° - теплота m m

плавления вещества, Дж/моль; A _mS° - энтропия T_m

плавления вещества, Дж/моль^К; T - температура плавления вещества, К; R – универсальная газовая постоянная, R = 8,314 Дж/моль·К.

Рассчитанная диаграмма состояния системы Cu₂O–Al₂O₃–ZrO₂ представлена на рис. 6. Координаты точек нонвариантных превращений I и II приведены в табл. 4. На диаграмме состояния помимо границ областей, равновесных с оксидным расплавом, нанесены изотермы для температур из интервала 1200–2600 °С с шагом 200 °С.

Рис. 6. Поверхность ликвидус диаграммы состояния системы Cu 2 O–Al 2 O 3 –ZrO 2

Координаты точек нонвариантных превращений на диаграмме состояния системы Cu 2 O–Al 2 O 3 –ZrO 2

Таблица 4

Наименование точки	Равновесие	Т , °С	x (Cu + )	x (Al3 + )	x (Zr4 + )
I	Ж–Cu 2 O–Al 2 O 3 –ZrO 2 тв. р	1105	0,8578	0,0598	0,0824
II	Ж–Cu 2 O–Al 2 O 3 –CuAlO 2	1150	0,8849	0,0844	0,0307

Выводы

Проведено термодинамическое моделирование линий ликвидус диаграмм состояния бинарных систем Cu2O–Al2O3, Cu2O–ZrO2 и Al2O3–ZrO2, а также поверхности ликвидус диаграммы состояния тройной системы Cu2O–Al2O3–ZrO2. Согласно результатам моделирования в тройной системе реализуется равновесие «оксидный расплав – чистый твердый оксид меди – чистый твердый оксид алюминия», которого нет в системе Cu2O–Al2O3. Показано, что тройная система характеризуется наличием двух точек нонвариантных превращений, положение которых смещено в сторону угла, вершиной которого является чистый оксид меди Cu2O. Температура точки тройного эвтектического равновесия составляет 1105 °С и, соответственно, численно меньше, чем для бинарных систем. Таким образом, стойкость футеровки из керамики Al2O3–ZrO2 при контакте с оксидом меди будет ниже, чем стойкость футеровки из чистого корунда или оксида циркония.

Работа осуществлена при финансовой поддержке РФФИ, грант № 13-03-00534.