Термодинамическое моделирование процессов взаимодействия кальция, магния, алюминия и бора с кислородом в металлических расплавах

Все более широкое применения бора в металлургии, особенно при выплавке малоуглеродистых сталей, связано с уникальной способностью бора повышать механические и эксплуатационные свойства стали при микродобавках бора в сталь, не превышающих 0,002–0,008 % по массе. При этом необходимо учитывать, что бор активно взаимодействует с серой, азотом и кислородом в стали, способен образовывать интерметаллиды с компонентами жидкого металла [1]. Сейчас путем лабораторных и промышленных экспериментов доказано, что положительное влияние на прочность, прокаливаемость, пластичность, снижение показателей анизотропии удается реализовать в технологии выплавки борсодержащей стали при наличии в металле так называемого свободного бора, бора, растворенного в металле, а не связанного в неметаллические включения [2–3]. Использование микролегирования стали бором, вводимым в пределах 0,001–0,025 % по массе, позволяет заменить в ряде случаев до 1,3 % никеля, 0,3 % хрома, 0,04 % молибдена на 0,001 % бора [4]. Прокаливаемость стали увеличивается с увеличением содержания углерода до 0,6 % [3, 5]. По мере работы над оптимизацией процесса микролегирования бором открываются все новые возможности использования бора. Бористые стали с содержанием бора 1–2 % являются эффективными поглотителями нейтронов и применяются в атомной энергетике [6, 7]. Использование далеко не полного перечня положительных свойств бора в металлургии требует дальнейшего изучения этих свойств. Для этого необходимо расширить круг изучаемых металлургических систем. Предварительно в работе [8] изучены и построены отдельные диаграммы состояний оксидных систем FeO–B2O3, B2O3–Al2O3, MnO–B2O3, SiO2–B2O3, MgO–B2O3, CaO–B2O3 с указанием сложных оксидных соединений, образующихся в этих системах. Также были построены поверхности растворимости компонентов в металлических системах (ПРКМ) для систем Fe–B–O, Fe–B–Si–O, Fe–B–Mg–O, Fe–B–Ca–O, Fe–B–Mn–O, Fe–B–Al–O [9]. Термодинамическая проработка литератур- ных и экспериментальных данных позволила установить зависимости констант равновесия, необходимых для расчетов, от температуры и параметры теории субрегулярных ионных растворов для оксидных систем. На основе этих расчетов установлено, что при современном уровне металлургических технологий можно добиться рафинирования стали по кислороду до 0,0001 %, по сере – до 0,002 % при реализации технологии печь-ковш. Для снижения концентрации азота в металле необходимо использовать присадки титана [10]. Это позволит снизить потери «эффективного» бора.

Для выяснения строения ПРКМ для бор- содержащих систем, раскисленных кальцием, алюминием и магнием, необходимо построить диаграммы состояния MgO–Al2O3–B2O3, CaO–Al2O3–B2O3, CaO–MgO–B2O3, т. е. существенным образом усложнить термодинамические расчеты. С использованием данных изученных ранее диаграмм состояний можно построить ПРКМ систем Fe–Mg–Al–B–O, Fe–Ca– Al–B–O и Fe–Ca–Mg–Al–B–O при фиксированном содержании бора ([B] = 0,001 мас. %), давления (1 и 1,5 атм) и температуры (1600 °С).

На рис. 1 представлены полученные расчетом координаты поверхностей ликвидус для систем MgO–Al 2 O 3 –B 2 O 3 , CaO–Al 2 O 3 –B 2 O 3 ,

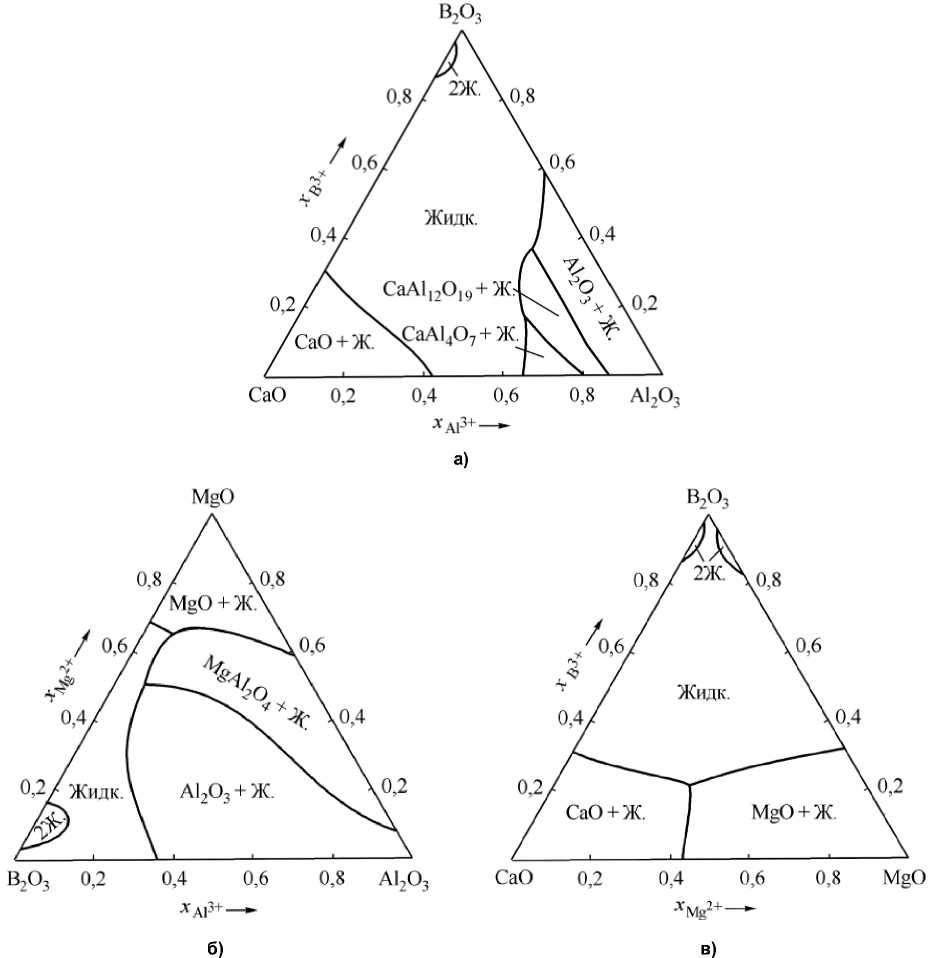
Рис. 1. Расчетные диаграммы состояний систем при 1600 °С: а) B 2 O 3 –Al 2 O 3 –CaO; б) B 2 O 3 –Al 2 O 3 –MgO; в) B 2 O 3 –MgO–CaO

CaO–MgO–B 2 O 3 при температуре 1600 °С, сведения о которых практически отсутствуют в научной литературе.

Диаграмма CaO–Al 2 O 3 –B 2 O 3 изучена Шефером и Куцелем только при 900–1500 °С [11]. В работе установлено существование двух тройных соединений: CaO·Al 2 O 3 ·B 2 O 3 и 2CaO·Al 2 O 3 ·B 2 O 3 . Температура плавления 2CaO·Al 2 O 3 ·B 2 O 3 по данным [11] на 9Al 2 O 3 ·2B 2 O 3 и расплав составляет 1015 °С. Соединение 9Al 2 O 3 ·2B 2 O 3 может существовать до температуры 1440 °С. Соединение 2CaO·Al₂O₃·B₂O₃ плавится инконгруэнтно при 1098 °С. Следовательно, в тройной диаграмме CaO–Al 2 O 3 –B 2 O 3 при 1600 °С возможно образование только алюминатов кальция, оксидов кальция и алюминия и наблюдалось расслоение расплава при высоком содержании В 2 О 3 в жидкости. В данной работе на основании двойных оксидных систем смоделирована тройная диаграмма состояний CaO–Al 2 O 3 –B 2 O 3 . Ранее тройные оксидные системы с B₂O₃ и FeO рассчитывали при 1600 °С, так как в литературе присутствует только одна диаграмма с FeO и B 2 O 3 – диаграмма FeO–B 2 O 3 –CaO, которая приводится именно при этой температуре, поэтому и наши расчетные тройные диаграммы состояний с B 2 O 3 приведены в [8] при 1600 °С. Энергетические параметры, подобранные в данной работе для системы CaO–Al 2 O 3 –B 2 O 3 , имеют следующие значения: Q 1123 = –110 000; Q 1223 = –72 000; Q 1233 = = –70 000 кал/моль.

На полях диаграмм (см. рис. 1) указаны химические оксидные соединения, которые могут быть в равновесии с оксидным расплавом (жидкостью). Так, на рис. 1а указаны поля изотермических фазовых равновесий

(CaO + Ж.), (CaAl 4 O 7 + Ж.), CaAl 12 O 19 + Ж.), (Al 2 O 3 + Ж.). Расслоение оксидного расплава обозначено символом (2 Ж.). Символом Ж. обозначены оксидные расплавы (CaO–Al 2 O 3 –B 2 O 3 ) для рис. 1а, (MgO–Al 2 O 3 –B 2 O 3 ) – для рис. 1б, (CaO–MgO–B 2 O 3 ) – для рис. 1в.

Диаграмма состояний B 2 O 3 –MgO–Al 2 O 3 (см. рис. 1 б) изучалась при более низких температурах [12–15], но полная диаграмма состояний системы B 2 O 3 –MgO–Al 2 O 3 не построена. В настоящей работе была построена эта диаграмма при 1600 °С. Подобранные в данной работе параметры теории субрегулярных ионных растворов для данной системы: Q 1123 = –50 000; Q 1223 = –100 000; Q 1233 = = –30 000 кал/моль.

Также были рассчитаны координаты поверхности ликвидус для диаграммы состояний системы B 2 O 3 –MgO–CaO (рис. 1в). Данная диаграмма была изучена в работе [16] только при 900 °С. Энергетические параметры, подобранные для этой системы в данной работе, имеют следующие значения: Q 1123 = –116 000; Q 1223 = –120 000; Q 1233 = –110 000 кал/моль.

В табл. 1 представлены необходимые для построения тройных диаграмм состояний значения зависимостей констант равновесия (плавления) от температуры. Круглые скобки обозначают жидкое состояние фазы, прямые – чистая твердая фаза.

В работе используется теория субрегулярных растворов с допущениями о квадратичной зависимости координационного числа раствора от химического состава взаимодействующих фаз. Основы теории и ее использование при определении термодинамических параметров взаимодействующих неметаллических фаз достаточно подробно изложены

Таблица 1

Термодинамические данные для реакций фазовых превращений, K – константа плавления оксидов и их соединений

№ Реакция плавления lg K = –A/T + B A B 1 |CaO| = (CaO) 2623 0,913 2 |B2O3| = (B2O3) 1257 1,738 3 |Al2O3| = (Al2O3) 5683 2,447 4 |CaAl2O4| = (CaO) + (Al2O3) 5507 0,482 5 |CaOAl4O7| = (CaO) + 2(Al2O3) 13 661 3,726 6 |CaOAl12O19| = (CaO) +6(Al2O3) 44 787 17,285 7 |MgO| = (MgO) 4044 1,305 8 |FeAl2O4| = (FeO) + (Al2O3) 9948 3,612 9 |MgAl2O4| = (MgO) + (Al2O3) 10 399 3,332 в монографии [17]. Используемые теоретические выкладки позволили построить темпера-турно-зависящую графику диаграмм фазовых равновесий, а также фазовую зависимость от исходного содержания бора. Полученные данные по структуре фазовых равновесий изучаемых систем позволяют в будущем учесть взаимодействие бора также с азотом и серой.

В табл. 2 приведены реакции, константы равновесия и их температурные зависимости, используемые для описания процесса раскисления стали кальцием, магнием, алюминием и бором. у - коэффициент активности иона металла в оксидном расплаве с использованием теории субрегулярных ионных растворов. Активности компонентов твердого раствора оксидов | FeO, CaO | приравнивали их ионным долям ( ^F^ = xFe2+|, ас^ = xСа2+| ), твердого раствора оксидов | FeO, MgO | также приравнивали их ионным долям а|FeO| = xF 2+|, aMgO| = xMg2+ . Твердые растворы | FeO, CaO | и | FeO, MgO | не смешиваются между собой в случае присутствия в системе и магния, и кальция. Активности компонентов твердого раствора шпинелей | FeAl2O4, MgAl2O4 | приравнивали их мольным долям ( а|FeAl2O4 = xFeAl2O4| , a|MgAl2O4| = xMgAl2O4|).

Опыт расчетов и анализов показывает, что при построении диаграмм рафинирования

Таблица 2

Зависимости констант равновесия реакций раскисления от температуры

№ Реакция Константа lg K = –A/T + B A B 1 (FeO) = [Fe] + [O] K1 - [Fe][O] T[o]/( ^Fe2,)r(.    ) 6320 4,734 2 (B2O3) = 2[B] + 3[O] K2 = [B]2 fB][O]3 Д OY( x2B2-)?(B2-) ) 44005 15,615 3 (Al2O3) = 2[Al] + 3[O] K3 = [Al]2fL][O]3fO]/(x     . , .) 58383 18,063 4 (CaO) = [Ca] + [O] K 4 = [Ca] f Ca][O] f O]/ (x(Ca2+) Y(Ca2+)) 31 480 12,55 5 (MgO) = [Mg] + [O] K 5 = [Mg] ./iмgliO] fO]/(x(Mg2.)7( Mg,.)) 22 457 6,545 6 |FeO|тв.р = [Fe] + [O] K 6 = [Fe][O] f 0^ x Fe2+| 8069 5,8 7 |CaO|тв.р = [Ca] + [O] K7 -[Ca]f[Ca][O]f[O]/xCa2+| 34103 13,46 8 |MgO|тв.р = [Ca] + [O] K 8 = [Mgl f[Mg][O] f[o]/xm,=.| 26500 7,85 9 |Al2O3| =2[Al] + 3[O] K9 - [Al]2f[Al][O]3f[0] 64000 20,48 10 |FeAl2O4|Tв.р = [Fe] + 2[Al] +4[O] K10 = [Fe][Al]2 f[Al][0]4 f0] /x|FeAl2O4| 74651 26,419 11 | MgAl2O41 Tв.р=[Mg]+2[Al] + 4[O] K ii-[ Mg] f[Mg][Ali2 f! Al][oi4 f; 0] /x MgA,1O4i 91 239 27,940 12 |CaAl4O7| = [Ca] + 4[Al] +7[O] K12 =[Ca ] f[Ca][Al]4 fAl][O]7 fO] 161775 52,34 13 |CaAl12O19| = [Ca] + 12[Al] +19[O] K13 =[Ca ] f\Ca ][Al]12 f[1 A2l][Ol19 f[1 O’ 426169 138,03 14 {CO} = [C] + [O] K14 = [C] f\c][O] f[ o]/ Pico. 1168 –2,07 15 {CO2} = [C] + 2[O] K15 = [C] f[c][O]2 fpj/PlCO.! 9616 2,51 16 {Ca} = [Ca] K16 - [Ca]f[Ca]/P{Ca) –1912 –2,69 17 {Mg} = [Mg] K17 = [Mg]f M,]/PiM# –6670 –6,48 стали, особенно для многокомпонентных реальных систем, необходимо установить соответствие между составом металла и химическим и фазовым составами неметаллических систем. При комплексном раскислении, как, например, в случае взаимодействия кислорода с магнием, бором и алюминием, состав жидкого металла должен быть сопряжен с оксидными фазами диаграммы состояний FeO–MgO–Al2O3–B2O3. В этом случае для определения фазового и химического состава оксидной диаграммы состояний требуется специальная работа. Необходимо знать диаграммы состояний FeO–MgO–Al2O3, FeO–MgO–B2O3, FeO–Al2O3–B2O3, MgO–Al2O3–B2O3. Причем необходимо знать также возможность образования в качестве неметаллических включений не только простейших оксидов, например, Al2O3 или B2O3, но и сложных соединений (FeAl2O4 и MgAl2O4).

Имеющиеся в справочных и научных изданиях сведения о высокотемпературных реакциях зачастую либо отрывочны, либо неизвестны, либо получены методом косвенных термодинамических расчетов. Для целей выполнения представленной работы необходимо получить сведения по химическим реакциям, представленным в табл. 1 и 2.

Особенности термодинамических расчетов, методы построения систем уравнений и их решения достаточно подробно изложены в монографии [17]. Активности компонентов металлического расплава рассчитывали с использованием параметров взаимодействия первого порядка (по теории Вагнера) [18–22]. Активности компонентов оксидных расплавов рассчитывали с использованием теории субрегулярных ионных растворов. Параметры теории для диаграмм состояний систем MgO–Al2O3–B2O3, CaO–Al2O3–B2O3, CaO–MgO–B2O3 приведены выше. Недостающие для расчетов энергетические параметры теории (для диаграмм, содержащих FeO) приведены в [8, 17].

На рис. 2 приведены диаграммы раскисления железа сплавами Mg–B–Al и Ca–B–Al. На полях диаграмм указаны названия фаз. Так, на рис. 2а в области I указаны составы жидкого металла, содержащего 0,001 мас. % бора, равновесного с оксидным расплавом (FeO, Al 2 O 3 , B 2 O 3 , MgO), в области II – с твердым раствором оксидов на основе MgO, в области III – с твердым шпинельным раствором, в области IV – с корундом. На линии no заданы составы металла, равновесного с твердым раствором оксидов и парами магния при давлении p _Mg = 1 атм. Аналогично линия n′o′ – для 1,5 атм. На линии om заданы составы металла, равновесного со шпинельным твердым раствором и парами магния при давлении 1 атм, на линии o′m′ – для 1,5 атм. Тонкими линиями на ПРКМ нанесены изотермы кислорода в логарифмических координатах. На осях рис. 2а нанесены концентрации компонентов в логарифмических координатах. Аналогичные обозначения и на рис. 2б (для случая раскисления кальцием, алюминием и бором).

На рис. 3 приведена ПРКМ системы Fe–Mg–Ca–Al–B–O при 1600 °С и фиксированных концентрациях [Mg] = 0,001 и [B] = = 0001 мас. %. Газовая фаза состоит из двух компонентов – паров магния и кальция. При общем давлении 1 атм p _Mg = 0,83 атм,

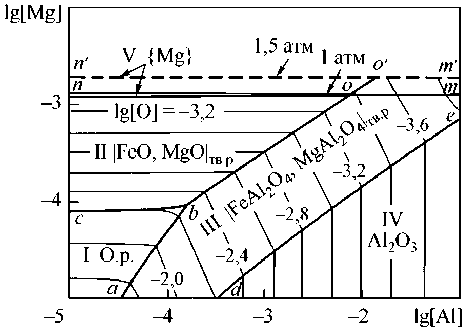
а)

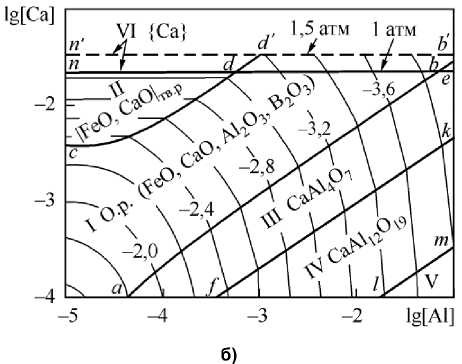
Рис. 2. Поверхности растворимости компонентов в металле (ПРКМ) при T = 1600 °С, [B] = 0,001 мас. % систем: а) Fe–Mg–Al–B–O; б) Fe–Ca–Al–B–O (V – Al 2 O 3 )

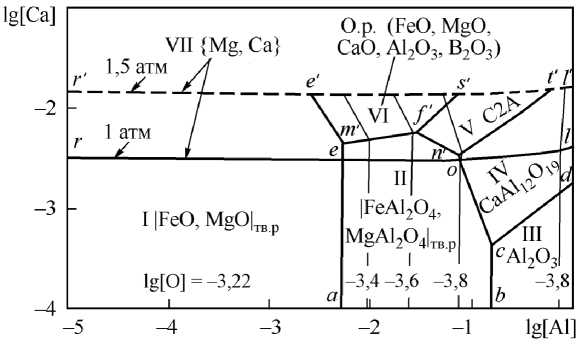
Рис. 3. ПРКМ системы Fe–Mg–Ca–Al–B–O, T = 1600 °С, [Mg] = 0,001, [B] = 0,001 мас. % (С2A – CaAl 4 O 7 )

p _Ca = 0,17 атм (линия reol ). В глубине металла возможно гидростатическое повышение давления. При общем давлении 1,5 атм p _Mg = 0,83 атм, p _Ca = 0,67 атм (линия r′e′s′t’l′ ).

Из рис. 2 и 3 видно, что равновесные по бору составы металла не содержат чистой фазы бора. Бор может входить в состав металлических расплавов и в небольших количествах расходоваться на раскисление металла. Основными же неметаллическими включениями будут магнезиальная шпинель, биалюминат кальция и жидкие оксидные включения (при [Ca] ≈ 0,001–0,005 и [Al] = 0,01–0,03 мас. %).

Заключение

Разработана методика расчета составов равновесного металла и шлака, при которых в основном бор не должен расходоваться на участие в оксидных фазах, а будет находиться в жидком металле. Построены диаграммы состояний систем MgO–Al 2 O 3 –B 2 O 3 , CaO–Al 2 O 3 –B 2 O 3 , CaO–MgO–B 2 O 3 при 1600 °С с использованием теории субрегулярных ионных растворов. Впервые построены поверхности растворимости компонентов для термодинамических систем Fe–Mg–Al–B–O, Fe–Ca– Al–B–O, Fe–Mg–Ca–Al–B–O при высоких температурах. Изучено влияние общего давления на растворимость магния и кальция в жидком железе.

Статья выполнена при поддержке Правительства РФ (Постановление № 211 от 16.03.2013 г.), соглашение № 02.A03.21.0011.