Термодинамическое моделирование системы железо - хром - никель - азот

Система железо – хром – никель является основой многих сталей и сплавов [1]. Некоторые из них в процессе изготовления подвергаются азотированию. Поэтому аналитический расчет пределов устойчивости фаз, образующихся в процессе азотирования металлических сплавов при различных температурах, представляет значительный практический интерес.

Для осуществления анализа фазового равновесия четырехкомпонентной системы необходимо иметь информацию о термодинамических харак- теристиках более простых трехкомпонентных систем. Значения термодинамических параметров, методика и результаты расчета изотермических сечений диаграмм состояния и их политермических разрезов при заданном содержании одного из компонентов для систем Fe–Cr–N, Ni–Cr–N, Fe–Ni–N и Fe–Cr–Ni представлены в работах [2–8].

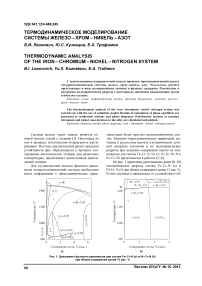
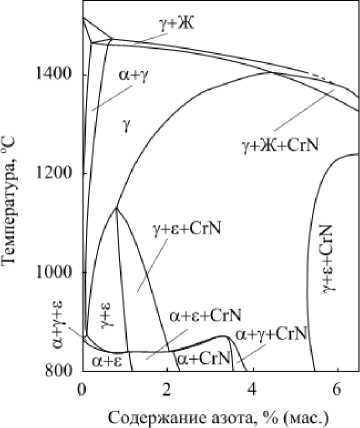
На рис. 1 приведены рассчитанные ранее [8–10] изотермические разрезы систем Fe–Cr–N ( а ) и Ni–Cr–N ( б ) при общем содержании хрома 13 мас. %. В этих системах в зависимости от условий могут об-

а)

Рис. 1. Диаграммы фазового равновесия для систем Fe–Cr–N (a) и Ni–Cr–N (б) при общем содержании хрома 13 мас. %

б)

Леонович Б.И., Кузнецов Ю.С., Трофимов Е.А.

разовываться следующие твёрдые фазы: феррит ( а ), аустенит ( у ), е - фаза на основе Ме₂N и нитрид хрома. Представленные графические зависимости демонстрируют последовательность образования этих фаз при повышении содержания азота при различных температурах.

В процессе анализа четырехкомпонентной системы Fe–Cr–Ni–N при выражении энергии Гиббса образующихся твердых фаз использована подрешеточная модель, согласно которой металлические элементы образуют одну структурную упаковку (первая подрешетка), а пустоты этой подрешетки и элемент внедрения – вторую подрешетку. Такие фазы можно представить общей формулой (Cr, Fe, Ni) _a (N, V ) _с , где значения а и с определяются числом мест (в молях) в подрешетках. При этом концентрации элементов (включая вакансии V ) в каждой подрешетке y можно связать с обычной молярной долей железа, никеля, хрома ( x i ) и азота ( x N ) и эта связь выражается следующим образом:

x

• У1 =;-----, У Fe ⁺ У Ni ⁺ У Cr = 1;

• ^{1    -} x N

ax

У N = —;----, У N ⁺ y v = 1.

c 1 - x N

Образование такого раствора можно представить смешением гипотетических бинарных соединений MeN и Me V , тогда молярная энергия Гиббса такой «пятикомпонентной» фазы может быть задана уравнением

G m = ^y Cr ^y N G Cr:N ^{+ y} Fe ^y N G Fe:N ^{+ y} Ni ^y N G Ni:N ⁺

^{+ y} Cr ^yV G Cr: V ^{+ y} Fe ^yV^G Foe: V ^{+ y} Ni ^yV^G Ni: V ⁺

^{+ RT [} a ( У Cr ln У Cr ⁺ У Fe ^ln У Fe ⁺ У Ni ^ln У Ni ) ] ⁺

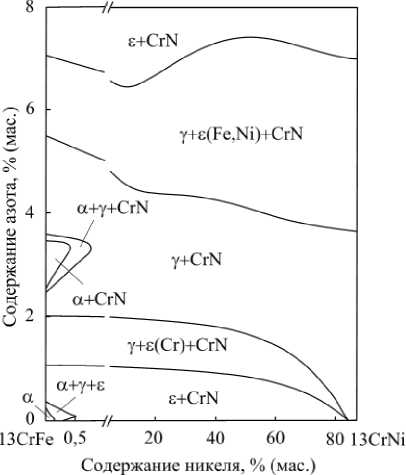
Рис. 2. Изотермическое сечение системы Fe–Cr(13 мас. %)–Ni–N для температуры 850 °С

+ RT [ с ( y N ln y N + y v ln У v ) ] + G mm ³⁶ + G m M^ar. (1) Здесь

G m ³⁶ = ^yCr^y Fe ( ^y N L Fe,Cr:N ^{+ y}V L Cr,Fe: V ) ⁺

^{+ y} Cr ^y Ni ( ^y N L Cr,Ni:N ^{+ y}V L Cr,Ni: V ) ⁺

^{+ y} Fe ^y Ni ^{( y} N L Fe,Ni:N ^{+ y}V L Fe,Ni: V ^{) +}

^{+ y} N ^yV ( ^y Cr L Cr,Fe:N ^{+ y} Fe L Cr,Ni:N ^{+ y} Ni L Fe,Ni:N ) ⁺

^{+ y} Cr ^y Fe ^y Ni ^yV^L Fe,Cr,Ni: V ^{+ У} Cr ^У Fe ^У N ^yV^LF e,Cr:N, V ⁺

^{+ y}Cr^У Ni ^У N З-УА зг.МН V ^{+ У} Fe ^У Ni ^У N ^yV^L Fe,Ni:N, V , ⁽²⁾ где L – энергии взаимодействия соседних частиц, находящих в разных подрешетках. В подстрочном индексе двоеточие разделяет подрешетки, а запятая – компоненты подрешетки.

Магнитная составляющая энергии Гиббса металлических сплавов рассчитывается по формуле

G m M^ar = RT ln ( в + 1 ) f ( т ) ,                     (3)

где т = T/T_C ( T_C - температура Кюри) и в (магне-тон Бора) являются параметрами модели и зависят от концентрации компонентов сплава:

^ОЦК = -310у Cr +1043у Fe + 575у Ni +

⁺ У Cr У Fe ^{[ 1650 + 550} ( У Cr ^- У Fe ) ] ⁺

• +yCryNi [2373 + 617 (yCr - yNi )] ;

в ОЦК = - о, 008 y Cr + 2,22 y Fe + 0,85 y Ni -

• - 0, 85УCrУFe + 4,0УCrУNi.

Для т <1:

79т-1 474 (1   ^Г т3 т9

+            1

140 p 497 ( p   J I 6 135 600 I

f (т) = 1--------^4^-----------4. (6)

Рис. 3. Диаграмма фазового равновесия системы Fe–Cr(13 мас. %)–Ni–N для содержаний никеля 20 % (сплошная линия) и 40 % (штриховая линия)

Для т >1:

f (^т)

( _-5 /г-15 /г-25 А /

I т        т         т I .

11 A

( 10   315 1500J/

где

A + ----- — — 1

1125 15975 (p J и pОЦК = 0,4.

С использованием приведенных соотношений была разработана модель, позволяющая оценить влияние никеля на характер фазовых равновесий, реализующихся в исследуемой системе.

Как показывает диаграмма (рис. 2), даже небольшие добавки никеля (менее 1 % по массе) приводят к дестабилизации феррита и повышению устойчивости аустенитной фазы.

Относительно низкие содержания в системе азота приводят к образованию фазы с гексагональной плотной упаковкой - твердого раствора ( е ) на основе (Cr,Fe) 2 N.

Рост содержания никеля в системе, согласно проведённым расчётам, дестабилизирует эту фазу (рис. 3).

При высоких содержаниях азота в системе е-фаза формируется на основе полунитрида (Fe,Ni)2N. Твёрдый раствор этого типа при всех возможных концентрациях никеля и в исследованном интервале температур характеризуется неограниченной растворимостью компонентов.

Выводы

Опираясь на ранее проведённые исследования по моделированию трёхкомпонентных систем, подрешеточную модель и литературные термодинамические данные, разработана термодинамическая модель системы Fe–Cr–Ni–N. Проведен термодинамический анализ и изучены фазовые равновесия в этой системе. Исследовано влияние никеля на изменение фазовых равновесий в сравнении с таковыми для тройной системы Fe–Cr–N. Результаты проведённых расчетов представлены в виде сечений диаграммы состояния изученной системы.

Работа осуществлена при финансовой поддержке РФФИ, грант № 11-08-12046-офи-м-2011.