Термодинамическое обобщение теории термоупругой диффузии для среды с изменяющейся плотностью

ВЕСТНИК ПНИПУ. МЕХАНИКА № 3, 2025PNRPU MECHANICS BULLETIN

Под теорией термоупругой диффузии, которая привлекает внимание многих исследователей, понимают теорию, описывающую взаимодействие между температурными полями и полями концентрации в деформируемых твердых телах, а также взаимное влияние всех этих полей друг на друга. Эта теория активно развивается, начиная с работ Лорда и Шульмана [1], Новацкого [2], Шермергора [3], Подстригача [4], Любова и Фастова [5; 6] и др.

В настоящее время существуют разнообразные обобщения классических теорий для сред с релаксацией тепла и массы [7; 8]; для анизотропных сред [9]; для сред с включениями [10]; для микрополярных сред [11]; для вязкоупругих сред [12; 13]; для пористых тел [14]; для сред при наличии электрических и магнитных полей [15; 16]. В работе [17] законы Фурье и Фика в модели термоупругой диффузии были модифицированы до включения производных по времени более высокого порядка от теплового потока, градиента температуры, потока компонента и градиента химического потенциала. В статье [18] исследуются задачи обобщенной теории термоупругой диффузии в рамках расширенной термодинамики с производными дробного порядка. В статье [19] теория термоупругой диффузии с дробными производными применяется для исследования поведения ламинированного композита при осесимметричной нагрузке. Развиваются аналитические и численные методы решения частных задач как в линеаризованной [20–25], так и в нелинейной [26–30] постановках.

Тем не менее в этой теории остаются вопросы, требующие специального обсуждения.

Цель настоящей работы состоит в том, чтобы выяснить роль сдвиговых компонент тензоров напряжений и деформаций во взаимодействии с полями температуры и концентраций, основываясь на методах термодинамики необратимых процессов. Оказалось, что для этого требуется лишь отказаться от приближения неизменной плотности среды в уравнения термодинамики.

Общие соотношения в уравнениях

Для построения уравнений теории термоупругой диффузии нам потребуются уравнение неразрывности

dρ =-ρ∇⋅V;                 (1)

dt уравнение баланса компонента

ρ dC ^k +∇⋅ J k =ω k ;             (2)

dt уравнение баланса внутренней энергии u в субстанциональной форме

n p — = -V. JT + £F, ■ Jk + о--VV ;       (3)

dt ы и уравнения движения dV p—= pF + V-о ,              (4)

dt где p - плотность; Ck - массовые концентрации компонентов; u - плотность локальной внутренней энергии; V - вектор скорости точек среды; Jk - диффузионные потоки компонентов; юk источники и стоки компонентов; JT - поток тепла; Fk - составляющая вектора внешних сил F , действующая на компоненту с номером к; о - тензор напряжений; V... = grad...; V-... = div....

Уравнения (1)-(4) являются следствием интегральных уравнений баланса [31; 32].

Для конкретизации уравнений воспользуемся термодинамикой, которая обладает много большими возможностями, чем полагают апеллирующие к ней многие исследователи.

Уравнение Гиббса в локальной форме имеет вид

n du = Tds + a 'p-1 deij + ^ gkdCk          (5)

к =1

удобна, если в изотермических условиях контролируются деформации, а энергия Гиббса g = u -Ts-2к.j, если в этих же условиях контролируются напряжения.

В первом случае уравнение Гиббса принимает вид:

n df = -sdT + 29dej+tgkdCk .         (9)

k =1

Во втором - n dg = -sdT-e,jd2j+tgkdCk .        (10)

k =1

Неравновесные уравнения состояния

В термодинамике имеются две группы определяющих соотношений - неравновесные уравнения состояния и соотношения, связывающие обобщенные потоки с обобщенными термодинамическими силами.

Поскольку f = f ( T , e j , C k ) , а (9) - это уравнение в полных дифференциалах, можем записать систему неравновесных уравнений состояния (УРС) в дифференциальной форме [33]

и включает только упругую часть тензора напряжений a j (то, что это упругие напряжения, будет видно из дальнейшего). Здесь e i, - компоненты тензора полных деформаций; g_k - химические потенциалы компонентов.

Уравнение (5) можно записать вдоль траектории движения центра масс:

| dT + e, Ck

d s de ,,

ids I de„ +---- dC,; c i' I5Ck £ k

, C k                             T ^{, e}

и =

du dt

т ds ^- 1 = Tn^{+a p}

^d Бу dC_k -+ ⁺ t gk-r dt к = 1 dt

Введем тензор напряжений Кирхгофа a e

2 j = — .                  (7)

p

Тогда вместо (5) запишем du = Tds + 2ydeij+t gkdCk .           (8)

k =1

Заметим, что пока не было никаких предположений относительно величины деформаций и/или сжимаемо-сти/несжимаемости среды.

Внутренняя энергия - функция переменных состояния - энтропии, компонент тензора деформаций и концентраций компонентов, и = и ( s , e ij , C _k ) . В целом выбор переменных состояния, очевидно, зависит от условий, в которых находится исследуемый объект.

Например, свободная энергия Гельмгольца

f = и - Ts

^{d 2}

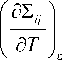
I ^д2 _и dT + 1

Ids ki.

^{d e} ki

Id C_k

I dC_k ; (11)

T ,e

~~~~~~~~~~

dg_k =\ — | dT + k Id T

^d g k de,-,

V ij / T , C l

—

d 6„+| — I dC .

ijl

■-' C l 7 T ,e

Множители при дифференциалах в (11), стоящие на диагонали, очевидно, определяют привычные термодинамические свойства - теплоемкость; упругие модули и индивидуальные термодинамические свойства компонентов. Подчеркнутые одинаковым образом слагаемые определяют физические коэффициенты, ответственные за перекрестные эффекты, связанные со взаимодействием разных физических полей.

Действительно, по определению,

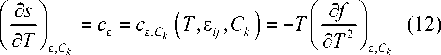
есть теплоемкость при постоянстве деформаций (аналог изохорной теплоемкости).

Следовательно,

T2 с s2 (б,Ck)-s1 (sCk) = J-CdT .

T 1 T

Это уравнение позволяет рассчитать энтропию, если теплоемкость в зависимости от термодинамических переменных состояния (в данном случае температуры, деформаций и концентраций) известны.

Второе слагаемое в первом уравнении (11) содержит производные

в k =

х1

Г C k J

Во второй группе УРС (11) осталось определить явно (через свободную энергию) упругие модули:

X1  =-Af f | = _-AfjTL-fe ]   ₍₁₃₎

де,, I          де Да T )     8 T 8е,, I la T I ^.

V ij У T , C k            ^- !        ⁷ V j J V      ^у е, C k

^- L Ав

= Г „

-j ав , ', C k

Используя определение (7), находим:

или

fe. 1    - Р - 1 '°7 -О_ ^Р=_ 1 _в t -0C ^а Р (14)

V дT L    дT р дT р2 дT р Рj р2 дT е,Ck

где в T = C j _kl ^T a ^т _к1 - «классический» тензор коэффициен

С „ ^-1 ав	=	Лав,		т , C k	a Ав		X Vde -j	У
а де -j	d f Лав>			с „ V ав -j	=	7о р V '"         у		т , C k

,

тов термоупругости [34-36]; а a Tl - тензор коэффициен

или

тов теплового расширения; C_i J _kl ^T - коэффициенты тен

зора упругих модулей. Индекс « T » в последнем случае указывает, что эти коэффициенты определены для изотермических условий.

Таким образом, «новый» тензор коэффициентов тер-

С „ = ^-j ав

1 1 do -

ij

^Рlд^е авJ т , C k

р ^C j ^ав

моупругости

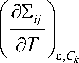
= -₽ T

явно зависит от плотности и от ее производной по температуре:

в T

= 1 в T +^ e   ;

р ^{P ij} р ² д т’

T ij

V а т

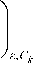
Найдем последнее слагаемое в первом уравнении (11):

" ^d s ¹ _ ^d a ^f _ a a f _ Га gk 1

S_k =         === —            (16)

^k Vd C k L 3 C_k а т а т a C_k La т J^ C ⁷

5 ^е                                                                                                      l

- это есть парциальные энтропии компонентов.

Следовательно, первое из УРС принимает вид

c ds = — dT + вTdб,-,- + skdCk.            (17)

ij ij k k

Аналогично (14) имеем

f8^ijI = a f af |= a f af I laCk I =ack las, 1 = аеДа ск I

v ^k TT ,е          ^k \                ij v ^k у

d g ^l = -в k , (18) ГГ J T , C l

где

в k

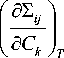
Lf i l = 1 в k ■ ° др a C k р р j р ² a C k ’

в k - «классические» тензоры концентрационной упругости компонентов,

СУ ij р2

^o j др

р ²

ар

^5е ав ^J т , C ,

0е»вД,

, '-k

Следовательно, вторая группа УРС принимает вид

d S j =-в T dT + С -j ав d Е ав -в ik dC k .        (22)

Оставшаяся группа уравнений состояния содержит уже известные коэффициенты и коэффициенты

I дgk I                      ~       ~ в! = ——   , конкретный вид которых определяется

¹   Г C l J т ,е

типом среды (идеальный раствор, регулярный раствор; неидеальный раствор) ([37-39] и др.):

T ,е

д I д ' II d C V C И _т ,

fAfd f II I⁵ C k V C l || _т ,

f ^d g l

Vd C k

=в k .

т ,e

Следовательно, dgk =-SkdT-вdеj+вkdC .         (23)

Учитывая определения «обобщенных» коэффициентов и тензора Кирхгофа, получим из (22):

р d o -j -^ d р = -в T dT + С -j ав d Е ав - в ik dC k =

f 1 т

- - в т + j

о аД р² а т _у

dT +

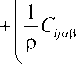
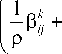
о ар р2 5Ck у

dC_k .

Группируем слагаемые:

Тогда вместо (24)–(26) получим

~ ^{d П ij d P} -^-[-P T dT + ^C j a₽ ^{d S} a₽ -P kj ^dCk ]“

P      P 2       P

c

ds ^_ 4 ^dT + ¹ C aX₽ ^P

T

-al	pp	dk +	dp	f sp 1
P 2	Is T'	I e, C k	^р)	ae Id c I k k , C k           [ k ) k ,e        _

d<5 = C R ij ij ap

j dp p ² d T

^{d e} ij ⁺ S k dC k ;

d e_ap-a T dT -Ya k dC_t ap ij                     ij

^{( k} )

То есть если плотность рассматривается как функция тех же самых термодинамических переменных состояния, то в общих определяющих соотношениях внешне ничто не изменяется. Однако появляется несимметрия в перекрестных коэффициентах.

Таким образом, имеем систему УРС в виде:

dg_k —- s_kdT - ¹ C_{a B}a ^k I j- ^^ d e„+p k dC . k k                   ij ap ae i                                  'i i

Ip p ^d C k )

Перейдем к изотропному телу:

a.- e ds = c- dT + 1 pT + Ц—P d£,-,+ s.dC. ;

T p ^ij p² dT ^ij k k

c 1

ds — — dT + — 3 K a_T8_it

T       [p ^{T ij}

a X

P ² d T ₎

^{d e} ij ⁺ s k ^dC k ;

d a j — 2 ц d e j + 5 _ij [ X d e ll - Kdw ] ;         (31)

d a j =-p d! + C j _ap d _{S ap}-P j dC_k ;        (25)

dg k ^{— -} s k ^{dT -}

¹ 3 K a k 5 ij +

dg k =- S k dT -1 ¹ p j + Ip

d £„+p k dC ;

ijll

P s C k )

"' |d d e j +P k dC i , P ^д C k )

где

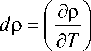
dT +

e, C k

dp I d    t , C

d e_aB+[— I dC_k . (27)

“ ^p Is C_k\     ^k

V ^k у T ,e

dw — 3 a _Tdk + ^ a _kdC_k ,

^{( k} )

И в (22), и в (25) приращения напряжений линейно связаны с приращениями деформаций, температуры и концентраций, т.е. являются упругими по определению.

Учитывая (15) и (21), найдем

^a t

^a k

или

или

T 22

T

и

P T = C jki a ^T _kl

1 T

= - P T + ^P

3 (a_n + ^a 22

~ ^ak V 3 k , V

ijkl

P

a

P ²

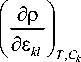
T ^a kl =

^a j dP _ - P ² 5 T "p

t i+aL dP kl ,

^J p d T

e a j I Sp I a t _ aa SP

2 Io | ^kl 2           ,

P l^de kl ) T,C_k        P ^{5 T}

I ^dP | kkT _ _Sp a .

peJ    kl at kl T,Ck

Аналогично найдем

Sp | _a k _ Sp ae„ I ij      d C_k '

ij T k

Благодаря этим соотношениями, можем принять

p — p ( t , C k ) .

– линейные коэффициенты теплового и концентрационного расширения.

Видим, что даже в изотропном теле энтропия и химические потенциалы компонентов зависят от всех компонент тензоров напряжений и деформаций. Это не противоречит принципам термодинамики, поскольку скалярная величина может зависеть от компонент тензора второго ранга.

Уравнение теплопроводности

Чтобы вывести уравнение теплопроводности, можно использовать разные последовательности выкладок. В настоящей работе уравнение теплопроводности найдем, используя (3) и (6):

ds ⁿ     dC

P ^T 37 ⁺ Lp g k^k ^— dt k —1        dt

Из (24) следует

n

— -V• JT +^Fk • Jk + I CT--W-ae k—1            [

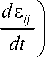
ds _— S ^dT ₊ f 1 R k | ^a ij ^p1 ^{d e} ij + s ^dC k dt T dt [p^{P j} p ² a T ) dt ^k dt

Поэтому уравнение (33) принимает вид:

Для изотропного тела имеем:

P T

' Cl dT

T dt

I

+ ^{f 1} в

Ip '

+f£ap^ d- j +s dC ' P 2 5 T I dt ^k dt

n dC

+ZPg ■ k —1

dT t\^v

P c, — + T 3 K a_T5_;, +

^E dt ^{T iJ}

e aij ap d£ p at J dt

n

—-v- jT + Z Fk • j k k—1

+ a i

a V e d -j a j axj       dt

aj. "              »

— - _r + Z F k ■ J k - Z hk ® k ^{a x} j k —1             k —1

Группируем слагаемые:

p c - dT + p T [ ¹ в T dt p

^{a 2}+£p hdC — p ² a t J dt tr ^k dt

n^„    f a v   e d j

— —V ■ Jy + У, F ■ J к + a ---a ----

^T £1 ^{k k} [ ^j a x j    ^j dt J

То есть слагаемое, отвечающее за связанность полей температуры и деформаций, теперь включает не только первый инвариант тензора деформаций, но и произведение компонент тензоров напряжений и деформаций, включая сдвиговые:

T 3 K a _T 5 „ +

i ^ ^d — з к _Or Td ₊^P „ . d f s p a T I dt ^T dt a ln T ^iJ dt

.

где h_k — g_k + Ts_k , по определению, парциальная энтальпия компонента k .

В упругом теле a j — a e .

Если примем, что компоненты тензора деформаций удовлетворяют соотношениям Коши (для других определений тензора деформаций выкладки становятся более громоздкими),

Этот факт обнаруживается безо всяких дополнительных предположений. Однако при выводе уравнений через потенциал Гиббса получаем несколько иной результат (см. далее), хотя все «новые» механизмы взаимодействия полей разной физической природы охраняются.

Уравнения для потоков тепла и компонентов

так что

и

^£ i

faи au,} +- ax,- aX;

ji

d - - i d a u i + a u - dt 2 dt f a x j a x_i ^

fav aj +- ax,    ax,- ji

a V _— 1

a x j 2

fav aV} i fav i-+j +i-ax -    ax,-     2  ax - v j i I v j

j i I

Как сказано выше, термодинамика предлагает еще одну группу определяющих соотношений. Это соотношения, связывающие потоки с обобщенными термодинамическими силами. В термодинамике необратимых процессов их выбирают из условия неотрицательности производства энтропии. Для простоты ограничимся бинарной системой и не будем учитывать внешние силы. В этом случае в линейном приближении без учета внешних сил имеем

J — LX + L XX, , ;

qqqqq 221

^J 2 ^— L 2 q^Xq ⁺ L 22 X 21 ,

где

то придем к уравнению теплопроводности вида

p c - dT + P T f ¹ в T + dt I p

- 3p1 d - j +vP hdC — p² a T ) dt h ^k dt

X     VT ■ X ^{Vl g} g ¹ . к r

X q T 2 ; X 21 T ^{; L} q 2    L 2 q ^.

Так как у нас всего два компонента, то справедливо

n

—-V- J T + У F k - J k .

k —1

C₁ + С 2 — 1 и J ₁ + J 2 — 0.             (37)

Воспользовавшись уравнением баланса компонента (2), найдем

Из системы УРС (31) для изотропного тела имеем

dg j — - s ₁ dT

-

P ^c -

dT + T dt	f P T + I	a j- P	ap a t ।	d j — dt
aj. —j + a x j	n Z F k k —1	- J k	n - Z k —1	h k ® k ,

¹ 3 K a^+^ ij- P ^J p ² a C

d £ j +в 1 dC + P 2 dC 2 ;

dg 2 — - s 2 dT

-

e

1         — ap

—3 K a,5- +4--

P ^J p ² a c 2 1

d £ j +в 2 dC +в 2 dC 2 ,

откуда следует

где J _qj – компоненты вектора плотности суммарного потока тепла:

^{V ( g} 2 ^{- g} 1 ) _T ^{— -}

^J qj ^{— J} Tj Z ^hk ^J k,J .                  ⁽³⁵⁾

( ^k )

1 t w           , т ^a «^- ap

— 3 K I a₇ - a )o„ + 2—z-- p ^{( 21}) ^j p² a c 2

+ ( -в 2 +в 1 +p 2 -P 2 ) v c 2 .

^V£ - ⁺

Следовательно, учитывая (37), находим: