Термодинамика химической и электрохимической устойчивости сплавов системы Mn-Si

Марганец в сплаве с кремнием используется в производстве рельсовой и конструкционной стали, им легируют сплавы на основе алюминия, магния и меди. Силикомарганец - ферросплав, основные компоненты которого железо, кремний и марганец, используется при выплавке стали как раскислитель и легирующая присадка [1].

Известно [2], что сплавы кремния с переходными металлами, в том числе и с марганцем, обладают необычным комплексом магнитных, электрических, механических свойств, а также высоким химическим сопротивлением и поэтому являются перспективными электродными материалами. Однако указанные свойства сильно различаются в зависимости от природы металлического компонента и его содержания в сплаве. Имеющиеся экспериментальные данные об электрохимическом поведении силицидов марганца [3] не охватывают весь возможный ряд силицидов и все возможные среды. Поэтому анализ коррозионно-электрохимического поведения сплавов марганца с кремнием различного состава представляет безусловный интерес. Кроме того, понимание термодинамических аспектов электрохимической устойчивости системы Мп—Si важно для дальнейшего изучения более сложных систем, например, системы Fe-Mn-Si.

Цель данного исследования - с точки зрения термодинамики рассмотреть вопрос электрохимической стойкости марганец-кремниевых сплавов в водных средах различного состава. В ходе решения этой задачи необходимо сначала разобраться с химическими и фазовыми равновесиями в системе Mn-Si и с механизмом окисления марганец-кремниевых сплавов кислородом воздуха.

Химические и фазовые равновесия в системе Mn-Si

Из анализа фазовой диаграммы состояния системы Mn-Si [4] следует, что при температуре 25 °C в системе существует семь интерметаллических фаз: МпцЗцд, MnSi, Mn5Si3, Mn5Si2, Mn3Si и две фазы переменного состава - rfMnySi?) и R(Mn6Si). Кроме того, возможно образование твёрдого раствора кремния в а-марганце с кубической решёткой (a-фаза). Область нестехиометрии r-фазы очень мала, поэтому при термодинамическом моделировании она будет считаться чистым силицидом Mn9Si2. По данным [5], R-фаза в точке, соответствующей равновесию с a-фазой, имеет состав Mno;85Sio,i5.

В литературе [5-9] имеется множество справочных данных об энергиях Гиббса образования силицидов марганца (табл. 1). Эти данные часто противоречивы, а для некоторых соединений они и вовсе отсутствуют. Поэтому появляется необходимость в проведении термодинамической оценки недостающих величин. Такая оценка была проведена с использованием формул Миедемы [8] и Истмена [10], а также с помощью метода Горичева [11]. При этом интерполяционная формула Лагранжа, используемая в этом методе, была модифицирована авторами таким образом, чтобы в качестве исходных данных в ней можно было использовать энергии Гиббса образования нескольких (а не только двух, как в оригинале) соединений. Модифицированный вариант расчётной формулы выглядит следующим образом:

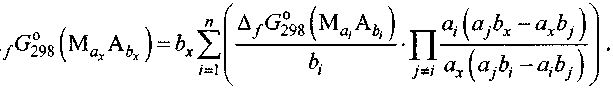
Здесь п - количество энергий Гиббса образования бинарных соединений, принимаемых в качестве достоверных исходных данных; М_а А_Л - формулы этих соединений (М - металл, А - атом более электроотрицательного элемента, а, и <5, - индексы при атомах М и А в соединении, соответственно); М^ А₆ - формула соединения, энергию Гиббса образования которого нужно оценить, а_х и Ь_х - индексы при атомах М и А в нём.

В качестве исходных данных для расчётов по формуле (1) были выбраны энергии Гиббса образования силицидов MnnSii9, MnSi, Mn5Si3 и Mn3Si из [7], как наиболее достоверные, по мнению авторов.

Таблица 1 Стандартные энергии Гиббса образования соединений из элементов

Стандартные энергии Гиббса образования соединений ( AyG^g), Дж/моль														Источник
Мпц8119	MnSi		Mn5Si3		Mn5Si2	Mn3Si		Mll9Si2		Mno^sSio.is	MnSiO3		Mn2SiO4
-954 878	-77 932		-280 518		—	-104 397		—			-1 240 827		-1 629 818 -1 671 327	[6]
-892 500	-76 701		-278 892			-107 758		—		—	-1 240 552		-1 632 190	[7]
—	-59 290		-207 480			-72 260		—		—	—		—	[8]
—	-92 612		-343 444			-141 997		—		—	-1 347 490		-1 779 298	[9]
-998 905 -965 780 -947 780 -935 780 -758 780 -344 780 -997 960 -979 960 -967 960 -790 960 -376 960	-78 200 -76 500 -68 100 -93 900 -74 700 -62 100 -78 280 -95 680 -69 880 -76 480 -63 880		-284 920 -273 120 -257 120 -23 0 720 -317 120 -243 520 -280 520 -264 520 -238 120 -324 520 -250 920			-103 240 -104 500 -107 300 -134 100 -144 100 -104 380 -107 180 -133 980 -143 980		-222 880		-16 850				[5]
-281 944	-48 107		-158 711		-74 502	-23 546		87 218		6 045			—	*
-892 500	-76 701		-278 892		-207 269	-107 758		-230 761		-17 823	—		—	**
-892 500	-76 701		-343 444		-265 000	-133 500		-240 000		-17 850	-1 240 552		-1 632 190	***
Стандартные энергии Гиббса образования соединений (AyG298), Дж/моль														Источник
МпО		Мп3О4		M112O3			MnO2		МП2О7			SiO2
-3 62 770		-1 281 955		-879 280			-465 370		-262 940			-851 279		[6]
-363 326		-1 282 885		-879 865			-466 662		—			-854 243		[7]
—		—		—			—		—			-805 067		[15]
-363 326		-1 282 885		-879 865			-466 662		-262 940			-805 067		***

* - расчёт по формулам Миедемы [8] и Истмена [10];

** - расчёт по методу Горичева [11] с использованием формулы (1);

*** _ окончательно скорректированные данные, используемые для дальнейших расчётов.

Результаты расчётов с использованием обоих методов также приведены в табл. 1. При этом результаты расчётов по формулам Миедемы и Истмена следует считать недостоверными, поскольку они слишком сильно отличаются от данных других источников.

0,85 Мп (а) + 0,15 Si (а)   R (Mn0 85Si0 ] 5 ),                                                  (2)

которая может быть получена путём комбинирования следующих реакций:

Физическая химия ________________________________________

0,85 Мп (а) + 0,1581(алмаз) ^> к(.Мп0 g5Si0 15),                                           (3)

Si (алмаз) —> Si (а) .                                                                          (4)

k_rG? реакции (3) - это, фактически, величина, равная AyG^Mn_0g5Si₀₁₅). По данным [5], она выражается уравнением AyG" (Мп_{0 85}Si₀₁₅ ) = -16700 - 0,5 Т, Дж/моль. Однако с учётом того, что по выполненным расчётам AyG2₉₈(Mn_0g5Si₀₁₅) = -17823 Дж/моль, это выражение было скорректировано:

ArG£(3) = AyG£(MnO85Sio l5) = -177OO-O,5r, Дж/моль.(5)

^_rGy реакции (4) есть энергия Гиббса фазового перехода кремния из кристаллической решётки алмаза в кубическую кристаллическую решётку. В литературе не имеется данных об этой величине, поэтому был предположен линейный характер её зависимости от температуры:

Энергия Гиббса реакции (2) может быть выражена через энергии Гиббса реакций (3) и (4):

AGy (2) = \Gt (3) - 0,15AGy (4) = (-0,5 - 0,15а) Г + (-17700 - 0,156) .(7)

Если принять R-фазу как чистое вещество Mno>85Sio,i5 (ак(мп0!!я„]5) = 1 Xто’ согласно уравнению изотермы химической реакции:

МЗД = -R7’ln^(2) = -ДПп-^-Ц^ = О^ЯПла^ + 0,15R74n aSi(ct).(8)

aMn(a) °Si(a)

Активности компонентов а-фазы рассчитываются в рамках однопараметрического приближения обобщённой теории «регулярных» растворов [12]:

ТгПпампЩ) = ^1птМп(а) + xSi(a) 'йгСО-(9)

7?rinasi(ot) = R74n Хд^ +^Мп(а)012Й) • где х - мольная доля, 5а(7) - энергия смешения компонентов раствора. Авторами предположен линейный характер её зависимости от температуры:

Q^T^cT^d .

После подстановки в уравнение (8) выражений (7), (9), (10)и(11)и учёта того факта, что в твёрдом растворе xMn(a) = 1 - xS1(a), получается окончательное выражение:

0,15аГ + 0,156 + с^0,85х§^а) + 0,15^1 -xSi(a)) ^Г + <7^0,85х^и) + 0,15^1-xSi(a)j ^ +

+17 700 + 0,5Т + 0,85RT In (1 - xS1(a)) + 0,157?Пп xSi(a) = 0 .(12)

Задача сводится к определению неизвестных параметров a, b, с, d уравнения (12). Необходимые для расчёта значения мольных долей кремния в точках, отвечающих равновесию твёрдого раствора с R-фазой, сняты с диаграммы состояния системы Mn-Si [4] и представлены в табл. 2.

Таблица 2

Мольные доли кремния, отвечающие равновесию a-фазы с R-фазой при различных температурах [4]

Г, К	473	523	573	623	673	723	773	823	873	903
-^Si(a)	0,0485	0,0500	0,0510	0,0515	0,0530	0,0550	0,0565	0,0590	0,0610	0,0625

После подстановки данных табл. 2 в уравнение (12) получена система из 10 уравнений с 4 неизвестными (a, b, с, d). В литературе [8] имеются данные об энергиях Гиббса фазовых переходов кремния из решётки алмаза в решётки г.ц.к., о.ц.к. и г.п.у. В предположении, что при нормальной температуре энергия Гиббса фазового перехода кремния из решётки алмаза в кубическую решётку должна быть сравнимой с этими величинами и составлять приблизительно 40 КДж/моль, в систему было введено дополнительное одиннадцатое уравнение: 298a + b = 40 000, Дж/моль.

С помощью метода наименьших квадратов [13] из полученной системы составлена система нормальных уравнений, содержащая 4 уравнения с 4 неизвестными. Данная система была решена методом Крамера [14]. Получены следующие результаты (Дж/моль): a = -174,66; Ъ = 92 049; с = 211,95; d = -219292. Таким образом, проведена термодинамическая оценка температурных зависимостей энергии смешения компонентов твёрдого раствора Mn-Si и энергии Гиббса фазового перехода кремния из кристаллической решётки алмаза в кубическую решётку:

Д;/Г" (Si (алмаз)   Si (а)) = 92 048-174,667, Дж/моль;                               (13)

g12(Mn-Si) = -219 292 + 211,957, Дж/моль.                                        (14)

Для того, чтобы определить мольную долю кремния в твёрдом растворе, отвечающую равновесию a-фазы с R-фазой, при комнатной температуре, уравнение (12) было решено относительно ^si(a) при известных значениях параметров a, b,c, dn условии 7 = 298 К. Найденный корень уравнения х§ц_а) =0,0456 . Активности компонентов твёрдого раствора в этой точке рассчитаны по формулам (9) и (10): a_Mn(a) = 0,832l,a_Si(a) = 3,835 • 10^2S. Таким образом, можно прийти к заключению, что в области низких температур (вплоть до комнатной) кремний практически не растворяется в марганце.

Химическая устойчивость

В соответствии с видом диаграммы состояния системы Мп-О [4] возможно существование следующих оксидов марганца: МпО, МщСД, Мп2Оз, МпО2 и Мп2О7. Кремний образует только один оксид SiO2. Также марганец и кремний могут образовывать смешанные оксиды (силикаты марганца) MnOSiO2 (Мп8Ю3)и 2МпО ■ SiO2 (Mn2SiO4) . Стандартные энергии Гиббса образования вышеперечисленных веществ, имеющиеся в различных источниках [6, 7, 9, 15], представлены в табл. 1. Для оксидов и силикатов марганца авторы считают наиболее достоверными данные из базы [7], для кремнезёма - величину из справоч ника [idj, поскольку именно это значение ^/^298 согласовано с экспериментально измеренным стандартным потенциалом кремниевого электрода (SiO2 + 4Н+ + 4е~ = Si (алмаз) + 2Н2О; Ф298 =-0,857В).

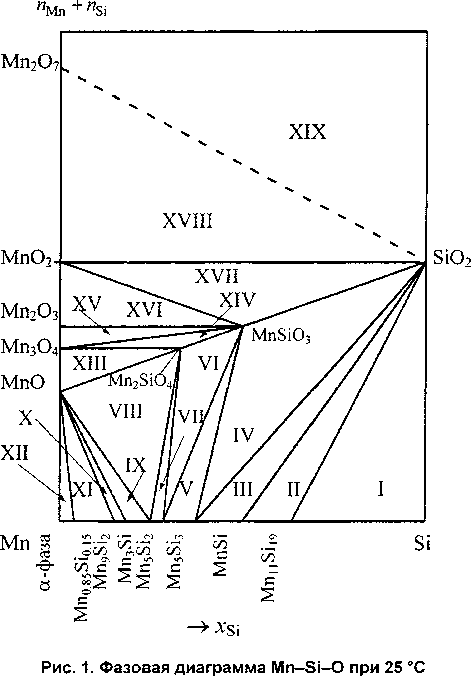
Для того чтобы построить фазовую диаграмму Mn-Si-O, необходимо разобраться с механизмом окисления марганец-кремниевых сплавов и подобрать последовательность равновесий, реализуемых в системе, таким образом, чтобы для каждой следующей реакции равновесное давление кислорода в газовой фазе было больше, чем для предыдущей. Было обнаружено, что полученные из [7] и рассчитанные термодинамические характеристики силицидов марганца не позволяют сделать это корректно. Поэтому было принято решение произвести корректировку энергий Гиббса образования некоторых соединений в пределах доверительных интервалов их возможных справочных значений. Окончательно откорректированные и использованные во всех дальнейших расчётах данные представлены в табл. 1 в строке ***. Фазовая диаграмма Mn-Si-O при 25 °C изображена на рис. 1. Рассчитанные характеристики трёхфазных равновесий системы представлены в табл. 3.

Физическая химия

Таблица 3

Характеристики трёхфазных равновесий системы Mn-Si-O при 25 °C

№ области	Равновесие	Уравнение реакции	Po, , атм	Равновесный состав фаз
I	81(алмаз)-Мп1i Si^-SiO2	81(алмаз) + O2 = SiO2	7,70-IO"142	xSi = 9 xMnHSi19= 9 xSiO2= 1
II	MnnSii9-MnSi-SiO2	Мпц8119 + 8O2 = 1 IMnSi + + 8SiO2	9,02-IO'14'	XMn,,Si19= 9 xMnSi = 9 XSiO2= 1
III	MnSi-Mn5Si3-SiO2	5MnSi + 2O2 = Mn5Si3 + + 2SiO2	2,50 -IO"38	xMnSi = 9 xMn5Si3= 9 xSiO2= 1
IV	Mn5Si3-MnSiO3-SiO2	2Mn58i3 + 4SiO2 + 11O2 = = 10MnSiO3	3,81 - IO136	xMn5Si3= 9 xMnSiO3= 9 ^Юг = 1
V	Mn5Si3-Mn5Si2- MnSiO3	6Mn5Si3 + 15O2 = 4Mn58i2 + + 10MnSiO3	5,36-IO"134	xMn5Si3= 9 xMn5Si2= 9 xMnSiO3=1
VI	Mn5 S i2-MnS iO3-Mn2SiO4	2Mn5Si2 + 2MnSiO3 + 9O2 = = 6Mn2SiO4	8,22-IO”133	xMn5Si2= 9 xMnSiO3= 9 xMn2SiO4=1
VII	Mn5Si2-Mn3Si- Mn2SiO4	Mn5Si2 + 2O2 = Mn38i + + Mn2SiO4	3,01-IO"132	xMn5Si2= 9 xMn3Si = 9 xMn2SiO4=1
VIII	Mn3Si-Mn2SiO4-MnO	2Mn3Si + 5O2 = 2Mn2SiO4 + + 2MnO	2,81-10431	■^Mn3Si — ■X'Mn2SiO4 ^’ хМпО ”
IX	Mn9Si2-Mn3Si-MnO	2MngSi2 + 3O2 = 4Mn3Si + + 6MnO	2,99-10"131	XMn9Si2= 9 xMn3Si = 9 xMnO = 1
X	Mno gsSiois—MngSi2— MnO	SOMno^sSiojs + 7O2= = 6Mn9Si2 + 4MnO	1,70-10428	"^Мпд 85Si015    ^’ ^'Mn9Si2 ^MnO = 1
XI	a-Mn085Si0i5-MnO	2Mn(o) + O2 = 2MnO	3,52-IO"128	хМп(«) =0,9544; XMn0 85Si015 =9xMnO=1
XII	a-MnO
XIII	MnO-Mn3O4- Mn2SiO4	6MnO + O2 = 2Mn3O4	2,36-10"68	хмпо = 9 хмп3о4= 9 xMn2SiO4= 1
XIV	Mn3O4-Mn2SiO4- MnSiO3	6Mn2SiO4 + O2 = 6MnSiO3 + + 2Mn3O4	1,41 - IO”38	ХМп3О4= 9 xMnSiO3= 9 xMn2SiO4=1
XV	Мпз O4—МП2О3— MnSiO3	4Mn3O4 + O2 = 6Mn2O3	1,32-IO26	хМп3О4= 9 хМп2О3= 9 xMnSiO3= 1
XVI	Mn2O3-MnO2- MnSiO3	2Mn2O3 + O2 = 4MnO2	1,82-1 O'9	хМп2О3= 9 хМпО2= 9 xMnSiO3=1
XVII	MnO2-MnSiO3-SiO2	2MnSiO3 + O2 = 2MnO2 + + 2SiO2	1,18-10""	хМпО, = 9 xMnSiO3= 9 xSiO2= 1
XVIII	MnO2-Mn2O7-SiO2	4MnO2 + 3O2 = 2Mn2O7	2J8-1078	хМпО2= 9 хМп2О7= 9 xSiO2= 1
XIX	МП2 O7—S i O2" {O2 }

Электрохимическая устойчивость

Основные химические и электрохимические равновесия в системе Mn-Si-H2O при 25 °C и 1 атм (воздух) представлены в табл. 4. Для расчёта термодинамических характеристик равновесий с участием ионов в растворе использована информация о стандартных электродных потенциалах из справочника [15].

Диаграмма потенциал - pH системы Mn-Si—Н₂О при 25 °C, 1 атм (воздух) и активностях ионов в растворе a_t = 1 моль/л изображена на рис. 2. На рис. 3 в увеличенном масштабе изображены сечения этой диаграммы в областях существования силицидов марганца.

Таблица 4

Основные химические и электрохимические равновесия в системе Mn-Si-H2O при 25 °C и 1 атм (воздух)

№ линии	Электродная реакция	Равновесный потенциал, В (н. в. э.) или pH раствора
1	2	3
a	2Н+ + 2<Г = Н2; РНг ~ 5 • ИГ7 атм	0,186-0,0591рН
b	О2 + 4Н+ + 4е“ = 2Н2О; ^ » 0,21 атм	1,219-0,0591рН
1	SiO2 + 4Н+ + 4е = Si + 2Н2О	- 0,857 — 0,0591рН
2	SiO^" + 6Н+ + 4е~ = Si + ЗН2О	-0,444 - 0,08865рН + 0,01481g aSjO2_
3	8SiO2 +1 IMnSi + 32Н+ + 32е = МП1 iSi19 + 16Н2О	-0,841-0,0591 pH
4	8SiO^ + HMnSi+ 48Н++32е” =Mn]]Si19 +24Н2О	-0,429 -0,08865рН + 0,01481gas.o2„
5	2SiO2 + Mn5Si3 + 8H+ + 8e" = 5MnSi + 4H2O	-0,805-0,059 IpH
6	2SiO|~ + Mn5Si3 +12H+ + 82O	-0,392 - 0,08865pH +0,01481g ц,.^
7	SiO2 + Mn5Si2 + 4H+ + 4e“ = Mn5Si3 + 2H2O	- 0,653-0,0591pH
8	SiO2 + 5Mn3Si + 4H+ + 4e~ = 3Mn5Si2 + 2H2O	- 0,526-0,0591рН
9	SiO2 + Mn9Si2 + 4H+ + 4e" = 3Mn3Si + 2H2O	-0,441-0,0591рН
10	7SiO2 +180Mn0g5Si0]5 + 28H+ +28e" = 17Mn9Si2 + 14H2O	-0,426-0,0591 pH
11	5MnSiO3 + 22H+ + 22e~ = Mn5Si3 + 2SiO2 +11H2O	- 0,772 -0,0591рН
12	5MnSiO3 + 18H+ + 225Si3 + 2SiO|~ + 9H2O	-0,922 - 0,04835рН - 0,005371g aSi02_
13	5MnSiO3 + 2Mn5Si2 + 30H+ + 30e" = 3Mn5Si3 + 15H2O	-0,741-0,0591 pH
14	MnSiO3 + 3Mn3Si + 6H+ + 6e" =2Mn5Si2 + 3H2O	- 0,690-0,0591рН
15	3MnSiO3 + 2Mn9Si2 +18H+ +18e" = 7Mn3Si + 9H2O	- 0,652 -0,0591рН
16	MnSiO3 + 2OMno 85Si015 + 6H+ + 6e~ = 2Mn9Si2 + 3H2O	-0,644- 0,059 IpH
17	3Mn2SiO4 + 18H+ + 18e“ = Mn5Si2 + MnSiO3 + 9H2O	- 0,723-0,0591рН
18	Mn2SiO4 + Mn3Si + 8H+ + 8e~ = Mn5Si2 + 4H2O	- 0,715 - 0,0591рН
19	3Mn2SiO4 + Mn9Si2 + 24H+ + 24e" = 5Mn3Si +12H2O	- 0,701-0,0591рН
20	7Mn2SiO4 +100Mn0 85Si015 + 56H+ + 56e“ = = 1 lMn9Si2 + 28H2O	-0,696-0,05 91 pH
21	Mn2SiO4+MnO + 10H+ +10e" ^Mn3Si + 5H2O	- 0,7004-0,0591рН
22	3MnO + 2Mn3Si + 6H+ + 6e“ = Mn9Si2 + 3H2O	- 0,7000-0,0591рН
23	7MnO + 3Mn9Si2 +14H+ +14e^ =40Mn085Si015 + 7H2O	-0,659- 0,0591рН
24	MnO + 2H+ + 2^=Mn(a) + H2O; aMn(ct) =0,8321	-0,651-0,0591 pH
25	Mn2+ +2e- =Mn(a); aMn(a) =0,8321	-l,183 + 0,029551gaMn2+
26	MnSiO3 + 2H+ = Mn2+ + SiO2 + H2O	pH = 2,66 -0,51g a ?+
27	Mn2SiO4 + 2H+ = Mn2+ + MnSiO3 + H2O	pH = 6,51-0,51gaMn2+
28	MnO + 2H+ = Mn2+ + H2O	pH = 8,99-0,51gtJMn2+
29	SiO3“ + 2H+=SiO2+H2O	pH = 13,94 + 0,5 lg«Si0|_

Физическая химия

Окончание табл. 4

1	2	3
30	Mn3O4 4 2H+ + 2е" = ЗМпО 4 Н2О	0,230-0,0591рН
31	Мп3О4 4 8Н+ 4 2е~ = ЗМп2+ 4 4Н2О	1,825 - 0,2364рН - 0,08865 ^^2+
32	Мп3О4 4 3MnSiO3 4 2Н+ 4 2е” = 3Mn2SiO4 4 Н2О	0,670 -0,0591рН
33	ЗМп2О3 4 2Н+ 4 2е“ = 2Мп3О4 4 Н2О	0,847-0,0591рН
34	Мп2О3 4 6Н+ 4 2е^ = 2Мп2+ 4 ЗН2О	1,499 - 0,1773рН - 0,05911g aMn2+
35	2МпО2 4 2Н+ + 2е“ = Мп2О3 + Н2О	0,952-0,059 IpH
36	МпО2 4 SiO2 4 2Н+ 4 2е" = MnSiO3 4 Н2О	1,068-0,0591рН
37	МпО2 4 SiO2^ 4 4Н+ 4 2е~ = MnSiO3 + 2Н2О	1,892 - 0,1182рН 4 0,0295 51g ag ю2_
38	МпО2 4 4Н+ 4 2е" = Мп2+ + 2Н2О	1,226 - 0,1182рН - 0,0295 51g «Мп2+
39	МпО2 4 4Н+ + е" = Мп3+ + 2Н2О	0,941 - 0,2364рН - 0,029551g «Мпз+
40	Мп3+ 4  = Мп2+	1,51040,05911g-^L ЯМп2+
41	МпО4 4 4Н+ 4 Зе^ = МпО2 4 2Н2О	1,695 - 0,0788рН + 0,01971g a
42	МпО4“ 4 4Н+ 4 2е" = МпО2 4 2Н2О	2,249 - 0,1182рН 4 0,029551g а^.
43	МпО^4е-=МпО^	0,588 4 0,05911g Mn0" ^MnO^

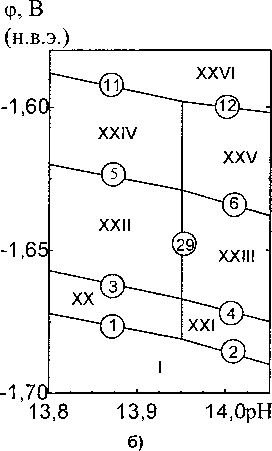
На диаграмме электрохимического равновесия системы Mn-Si-H2O (рис. 2, 3) можно выделить 42 области термодинамической устойчивости различных фаз: I — а-фаза (Мп) + R-фаза (Mno^sSiojs) + г-фаза (Mn9Si2) + Mn3Si + Mn5Si2 + Mn5Si3 + MnSi + MnnSiig + Si; П - Mn'+ 4 + MnOj85Sio,i5 + Mn9Si2 + Mn3Si + Mn5Si2 + Mn5Si3 + MnSi + MnnSi19 + Si; III - Mn2+ + Mno^sSiojs + + Mn9Si2 + Mn3Si + Mn5Si2 + Mn3Si3 + MnSi + MnnSii9 + SiO2; IV - Mn2+ + Mno^sSiojs + Mn9Si2 4 + Mn3Si + Mn5Si2 + Mn5Si3 + MnSi + SiO2; V - Mn2+ + Mno^sSiojs + Mn9Si2 + Mn3Si + Mn5Si2 4 + Mn5Si3 4~ SiO2; VI — Mn 4" Mn9 ssSio 15 4- Mn9Si2 4- Mn3Si 4" Mn3Si2 4- SiO2; VII — Mn + Мпо ssSio 15 4 4- Mn9Si2 4- Mn3Si 4- SiO2; VIII - Mn2+4 Mno^sSiojs 4- Mn9Si2 4- SiO2; IX - Mn2+ 4- Mno^sSiojs 4- SiO2; X - Mn3+ 4- MnossSiois 4- SiO2; XI - Mn2+ 4- MnossSiois 4- Mn9Si2 4- Mn3Si 4- Mn5Si2 4 Mn5Si3 4 4- MnSiO3; XII - Mn2+ + Mno,ssSioj5 4- Mn9Si2 4- Mn3Si 4- Mn5Si2 4 MnSiO3; XIII - Mn2+ 4 Mno,85Sioj5 4 4 Mn9Si2 4 Mn3Si 4 MnSiO3; XIV - Mn2+ 4 Mno ssSio 15 + Mn9Si2 4 MnSiO3; XV - Mn2+ 4 Mn0 ssSio 15 + 4 MnSiO3; XVI - Mn2+ 4 Mno.ssSiojs 4- Mn9Si2 4 Mn3Si 4 Mn5Si2 4 Mn2SiO4; XVII -’Mn2+ 4 4 Mno^sSiojs + Mn9Si2 4 Mn3Si + Mn2SiO4; XVIII - Mn2+ 4 Mno^sSiojs + Mn9Si2 4 Mn2SiO4; XIX -Mn2+ 4 Mno.ssSiojs + Mn2SiO4; XX - a 4 Mno^sSiojs + Mn9Si2 4 Mn3Si 4 Mn5Si2 4 Mn5Si3 4 MnSi 4 4 MnnSi]9 + SiO2; XXI - a 4 Mno.ssSiojs + Mn9Si2 4 Mn3Si 4 Mn5Si2 4 Mn5Si3 4 MnSi 4 MnnSii9 4 4 SiO2”; XXII - «4 Mno.ssSiojs + Mn9Si2 4 Mn3Si 4 Mn5Si2 4 Mn5Si3 4 MnSi 4 SiO2; XXIII - a 4 + Mno.ssSiojs + Mn9Si2 4 Mn3Si 4 Mn5Si2 4 Mn3Si3 + MnSi 4 SiO|” ; XXIV - a 4 Mno.ssSiojs + Mn9Si2 4 4 Mn3Si 4 Mn5Si2 + Mn5Si3 4 SiO2; XXV - a 4 Mno^sSiojs + Mn9Si2 4 Mn3Si 4 Mn5Si2 4 Mn5Si3 4 4 SiO2“; XXVI - a 4 Mno.ssSiojs + Mn9Si2 4 Mn3Si 4 Mn5Si2 4 Mn5Si3 4 MnSiO3; XXVII - a 4 4 Mno^sSiojs + Mn9Si2 4 Mn3Si 4 Mn5Si2 4 MnSiO3; XXVIII - a 4 Mno^sSiojs + Mn9Si2 4 Mn3Si 4 4 Mn5Si2 4 Mn2SiO4; XXIX - a 4 Mn0 ssSio is + Mn9Si2 4 Mn3Si 4 Mn2SiO4; XXX - a 4 Mn0 8sSi015 + 4 Mn9Si2 4 Mn3Si 4 Mn2SiO4 4 MnO; XXXI - a 4 Mno.ssSiojs + Mn9Si2 4 Mn2SiO4 4 MnO; XXXII -a 4 Mn0 ssSio 15 + Mn2SiO4 4 MnO; XXXIII - Mn0 ssSio 15 + Mn2SiO4 4 MnO; XXXIV - Mn0 ssSi0 is + 4 Mn2SiO4 4’ Mn3O4; XXXV - Mno^sSiojs + MnSiO3 4 Mn3O4; XXXVI - Mno.ssSiojs + MnSi63 4 4 Мп2О3; XXXVII - Mno^sSiojs + MnSiO3 4 MnO2; XXXVIII - Mno.ssSiojs + MnO2 + SiO2; XXXIX -Mno^sSiojs + MnO2 4 SiC)| ; XL - Mno.ssSiojs + SiO2 4 MnO4 ; XLI - Mno.ssSiojs + MnO4”, SK)|- ; XLII - Mno.ssSiojs + MnO4, SiO2" .

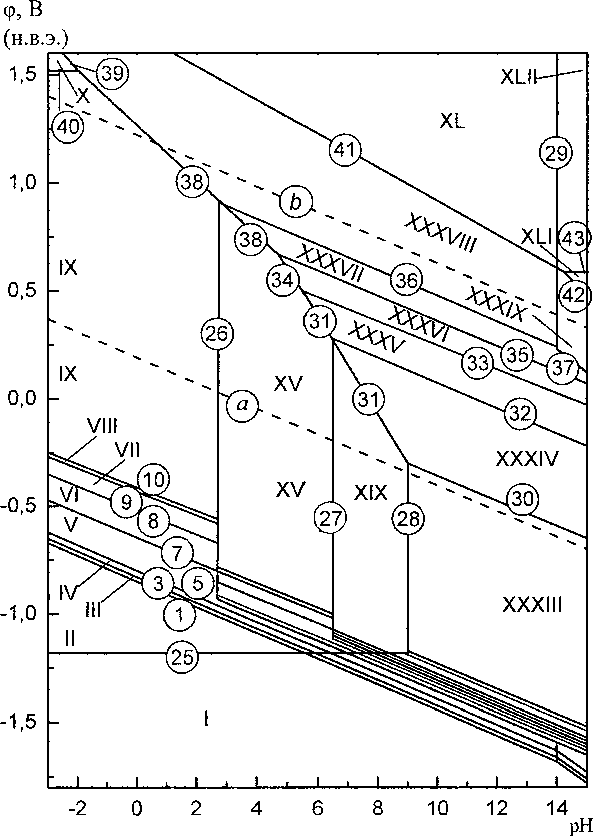
Рис. 2. Диаграмма потенциал - pH системы Mn-Si-H2O при 25 °C, 1 атм (воздух) и я,- = 1 моль/л

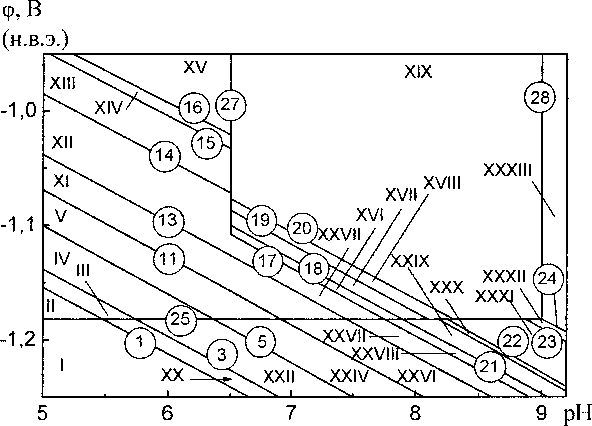
Рис. 3. Сечение диаграммы потенциал - pH системы Mn-Si-H2O при 25 °C, 1 атм (воздух) и я,- = 1 моль/л в области существования: а) силицидов марганца; б) ионов S1O3"

Физическая химия

Обсуждение результатов

Анализируя фазовую диаграмму Mn-Si-O, можно прийти к следующим выводам: окисление марганец-кремниевых сплавов начинается при давлениях кислорода в газовой фазе выше 7,70 -1О¹⁴² атм. Поскольку для окисления МпО₂ до Мп₂О₇ необходимо давление кислорода, равное 2,18-Ю⁷⁸ атм, то окисление на воздухе (Р_о^ =0,21 атм) должно завершиться образованием оксидов МпО₂ и SiO₂. Однако, поскольку в реальных условиях термодинамическое равновесие недостижимо, оксидная плёнка на сплавах может содержать и другие оксиды, а также силикаты марганца. Её конкретный состав будет очень сильно зависеть от содержания кремния в сплаве. Так, если кремния в сплаве не более 25 ат. % (его недостаточно для образования силицида Mn₃Si и силицидов с более высоким содержанием кремния), то наиболее вероятными продуктами окисления будут оксиды марганца и Mn₂SiO4. При увеличении содержания кремния в сплаве возможно образование в составе оксидной плёнки MnSiO₃ и SiO₂.

Коррозионно-электрохимическое поведение марганец-кремниевых сплавов будет определяться кислотностью среды и установившимся в ней значением стационарного потенциала. В кислых средах будет наблюдаться селективная коррозия марганца, и переход его в раствор в виде катионов Мп2+ (области II—IX на рис. 2, 3), а кремниевая составляющая сплава будет окисляться до SiO2 (в работе [3] это подтверждено экспериментально). В нейтральных и щелочных средах, в зависимости от содержания кремния в системе и конкретных условий, окисление может заканчиваться образованием силикатов Mn2SiO4 или MnSiO3. Защитная плёнка из этих силикатов является более стойкой в химическом и электрохимическом плане, нежели SiO2, поскольку она не окисляется до SiO2-.

Наличие множества различных справочных данных и необходимость оценивания и корректировки некоторых термодинамических величин не позволяют говорить о том, что предложенная авторами работы картина окисления марганец-кремниевых сплавов является окончательной и безусловно верной. Теория не даёт однозначного ответа по поводу некоторых конкретных равновесий, особенно в областях существования низших силицидов марганца. Несмотря на это общие закономерности коррозионно-электрохимического поведения системы Mn-Si выявлены, показано, что химическая и электрохимическая устойчивость марганец-кремниевых сплавов выше, чем таковая для чистых марганца и кремния, и что конкретный состав продуктов окисления определяется содержанием обоих компонентов в сплаве.

Выводы

• 1.    Рассмотрены химические и фазовые равновесия в системе Mn-Si при 25 °C. Проведено согласование и прогнозирование термодинамических свойств компонентов системы, проведена оценка предельной растворимости кремния в марганце при комнатной температуре.

• 2.    Построена фазовая диаграмма Mn-Si-O при 25 °C. Рассчитаны характеристики трёхфазных равновесий системы, показано, что химическая устойчивость сплавов системы Mn-Si определяется содержанием в сплаве обоих компонентов.

• 3.    Построена диаграмма потенциал-pH системы Mn-Si-H₂O при 25 °C, 1 атм (воздух) и а, = 1 моль/л. Показано, что в кислых средах первичная пассивационная плёнка на сплавах Mn-Si представляет собой чистый кремнезём. В нейтральных и щелочных средах она в зависимости от содержания кремния в сплавах может состоять как из чистых оксидов марганца и кремния, так и из силикатов марганца.