Термохимические характеристики силицидов хрома при стандартных условиях

Среди разнообразных направлений использования хрома в металлургии наибольший удельный вес (~75 %) занимают окислительно-восстановительные процессы с участием оксидов хрома. В ходе процесса восстановления оксида хрома свободным кремнием при высокой температуре в качестве промежуточных продуктов образуются различные силициды хрома. Некоторые из них имеют самостоятельное значение.

В системе «хром - кремний» [1] обнаружены следующие силициды хрома, устойчивые в твердом состоянии: Cr3Si, Cr5Si3, CrSi и CrSi2. Кроме того, по данным [2, 3] в системе возможно существование Cr2Si. В опубликованных результатах исследований [4] приведены экспериментальные значения термодинамических свойств CrSi2, CrSi, Cr5Si3 и Cr3Si, определенные методом ЭДС. Исследования строения и свойств проводились главным образом сплавов хрома с кремнием в жидком состоянии [5]. Термодинамические свойства соединений, оцененные по разным литературным источникам, имеют существенные расхождения в значениях.

Термодинамический анализ и выбор рациональных условий проведения процесса силикотер-мического восстановления Сг2О3 при производстве металлического хрома осложнен отсутствием базовых структурных и термодинамических параметров для силицидов хрома.

Таким образом, в справочной литературе не содержится достаточно полных сведений, необходимых для глубокого термодинамического анализа рассматриваемой системы. В то же время отсутствуют убедительные методики расчета термодинамических характеристик (5°, Ау//° и b_fG°) для веществ, находящихся в кристаллическом состоянии, отвечающие имеющимся справочным данным [6,7].

В разработанных математических моделях расчета термодинамических характеристик используются некоторые общие понятия и обозначения.

• 1.    Состав бинарных кристаллических соединений Ме^А, приводится к виду МеА^ или МеА., т.е. все расчеты ведутся на 1 моль металла в соединении. Подобный прием широко используется при проведении термодинамических расчетов, поскольку позволяет сравнивать свойства соединений разнообразного состава.

• 2.    Поле диаграммы «свойство - состав» разбивается на области твердых растворов (ОТР-1, ОТР-2 и т.д.), разделяемых кривыми равновесия между ними. В одну ОТР объединяются соединения, имеющие один и тот же, либо близкий тип кри-

• сталлической структуры. Границей диаграммы является дальтонид с максимальной степенью окисления (например, СгО3 в системе Сг - О).

• 3.    В каждой области выделяется кристаллообразующий (КО) компонент. В первой ОТР кристаллообразующим всегда является сам металл. Кристаллообразующим компонентом в последующих областях твердых растворов (ОТР-2, ОТР-3 и т.д.) является наиболее термодинамически устойчивый дальтонид.

• 4.    Постепенное изменение состава внутри каждой ОТР приводит к тому, что меняется характер атомно-молекулярного взаимодействия, а это в свою очередь приводит к преобразованию пространственного расположения частиц. Количественно этот переход от одной кристаллической формации к другой отражается объемной структурной постоянной К_т являющейся специфической величиной для каждой конкретной области. Для определения К„ используются структурные константы к [8] одноразмерных (простые вещества) и разноразмерных (сложные вещества) частиц, характерных для примитивной - &п_РНМ, тетраэдрической - А_те71мэд, октаэдрической - к_окт, ОЦК - Ар_цк и ГПУ - Л_ГПу структур.

Разработанные математические модели базируются на имеющихся экспериментальных (справочных) данных [1-3, 9-12]. Значения С_р, S, bfS выражены в Дж-моль ’-К¹, А/Я, A^G-в кДж-моль '-К¹.

ТЕПЛОЕМКОСТЬ

Математическая модель расчета теплоемкости кристаллических соединений подтверждена многочисленными справочными данными на примерах оксидов 5-, р- и (/-элементов произвольного состава, а также на трехкомпонентных оксидных ферри-и хромишпинелях, ильменитах [6, 13]. Эта модель успешно использована при расчетах теплоемкости кристаллических нитридов марганца. В работе [14] была доказана возможность применения модели для случая, когда компонент А — твердое вещество, на примере карбидов хрома произвольного состава.

Расчет молярной теплоемкости для соединения любого состава в пределах одной ОТР (если компонент А при стандартных условиях - кристаллическое вещество) проводится по уравнению:

С;’(МеАх) = Ср1(КО)±—т---—  (1)

"        " Я„[х„СДА)+СДКО)]

где Ср (КО) - молярная теплоемкость кристаллообразующего вещества; хк0 их- мольная доля компонента А в КО и в рассматриваемом соединении соответственно; *„ - координата внешней границы рассматриваемой ОТР.

Для расчетов уравнение (1) приводится к виду:

С"¹ (МеА_х) = а_с + Ь_сх .                   (2)

Совместное решение ур. (2) для смежных областей дает возможность аналитически определить координаты их границ.

В табл. 1 приведены исходные справочные данные для силицидов хрома, являющиеся опорными для проверки математических моделей. Из анализа кристаллических структур силицидов хрома следует, что диаграмма С”¹ - х должна состоять из двух ОТР.

Первая ОТР: Cr-Cr4Si3 (переход структуры: ОЦК -> тетрагональная);

вторая ОТР: Cr4Si3-CrSi2 (тетрагональная -+ ГПУ).

ОТР-1: Сг - СгЛГ (х = 0+0.75). КО - Сг

Переходу от Сг (ОЦК) к Cr4Si3 (кубич.) соответствует объемная структурная постоянная

= W-2-^кч = 2^3-1)-|-6 = 1,09808 .

Из анализа взаимосвязи структура-состав (табл. 1, колонки 1 и 2) следует, что граница раздела ОТР проходит через состав Cr4Si3 (CrSio^s), где происходит изменение кристаллических сингоний. Однако для Cr4Si3 данные отсутствуют, поэтому используется величина С° (Cr5Si3).

Ур. (1) для данной области принимает вид: с;1 (CrSi) = с;1 (сг) —=----—=,

(х„ = 0,6).(3)

После подстановки численных величин в ур. (3): с;1 (CrSix) = 0,04246--;------г;

• ^{р v 7}           1,09808(0,6-20,042+23,550)

С;1 (CrSix) = 0,04246 - 0,05729*.(4)

OTP-2: CnSh - CrSi_? (х = 0,75+2.0). КО - CrSi

Переходу от Cr4Si3 (тетраг.) к CrSi2 (ГПУ) соответствует комбинация линейных структурных констант

^2 ⁼ ^тетраг " ^ГПУ-6 " ^ККЧ ⁼ СГ ""’6 = 1,81066. о -V2 —1

Для ОТР-2 расчетное ур. (1) принимает вид: с;1 (CrSi) = с;1 (CrSi)

' ^[x„C„(Si)+Cp(CrSi)] (х„ = 2,0).(5)

После подстановки численных величин в ур. (5) получим:

с;1 (CrSi ) = 0,02217--;г;

’           1,81066(2,0-20,042+45,104)

C;*(CrSix) = 0,02865-0,00648*.(6)

Результаты расчетов по ур. (4) и (5) приведены в табл. 1 и на рис. 1.

Совместное решение уравнений, описывающих зависимости обратной теплоемкости от соста-

Таблица1

Стандартные молярные теплоемкости Ср силицидов хрома

№ Вещество Структура, [2, 9, 11] С, [2, 3J0] С-1 Сч УР- (4), (6) Ср, расч. 1 2 3 4 5 6 1 Si ГЦК-4 (алмаз) 20,042+0,042 2 Сг ОЦК-2 (a-Fe) 23,550+0,126 0,04246 3 Cr3Si CrSio,33333 кубич.-4 (Cr3Si) 88,282+0,460 29,427 0,03398 0,03393 88,426 29,475 4 Cr2Si CrSio.s кубич.-4 (CaF2) 0,02966 67,431 33,715 5 Cr5Si3 CrSio.6 тетрагон. (W5Si3) 184,389+0,920 36,878 0,02712 0,02710 184,502 36,900 6 Cr4Si3 CrSio,75 тетраг. 0,02379 168,138 42,034 7 CrSi кубич.-4 (FeSi) 45,104+0,251 0,02217 0,02217 45,106 8 Cr3Si4 CrSii,33333 куб.-8 (MgAl2O4) 0,02001 149,925 49,975 9 Cr2Si3 CrSiL5 ГПУ-8 (Mn2O3) 0,01893 105,652 52,826 10 CrSi2 ГПУ-6 (a-SiO2) 63,597+0,335 0,01572 0,01569 63,735 ва силицидов хрома для граничащих областей твердых растворов, позволяет аналитически определить состав границы между ОТР. Так, из ур. (4) и (6) находим состав, отвечающий границе между ОТР-1 и ОТР-2 х]-2 = 0,72228, что близко к составу предположенного Cr4Si3 (CrSi0>75)-

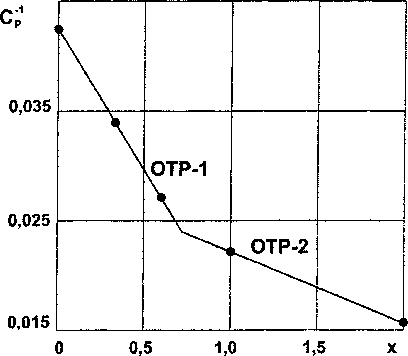
Рис. 1. Зависимость обратной теплоемкости силицидов хрома (CrSi,) от состава (• - эксперимент, „ - расчет)

СТАНДАРТНАЯ ЭНТРОПИЯ

Одной из важнейших термодинамических и теплотехнических характеристик веществ является энтропия. Наибольший теоретический и практический интерес представляет расчет энтропии веществ, находящихся в конденсированном состоянии, так как для веществ в газовой фазе вопрос решен методами статистической физики.

Основные положения предлагаемой математической модели [15].

• 1.    Абсолютная энтропия сложного вещества складывается из двух независимых величин: AS. (от mass), связанной с массой и AS. (от interaction), определяемой межчастичным взаимодействием:

• 2.    Обратная величина &S_in бинарного вещества равна сумме обратных величин компонентов с учетом состава и кристаллических структур. В общем виде расчетное уравнение зависимости от х (для случая, когда компонент А при стандартных условиях - кристаллическое вещество) выглядит [14]:

S = M_m+^S_in.                      (7)

Массовая составляющая энтропии рассчитывается по уравнению:

\8„,=^М,                (8)

где R - универсальная газовая постоянная; М - относительная атомная (молекулярная) масса, отнесенная к одному молю металла. /XS_in рассчитывается как разность известных величин S и hS_m.

AS71(MeAj = A57*(KO)±

+--------^2--------- (9)

^[xnAS/„(A) + AS.(KO)]-

Для расчетов ур. (9) приводится к более удобному виду:

№ДМе^ = а₅±Ь₅х.            (10)

Совместное решение ур. (10) для смежных областей дает возможность аналитически определить координаты их границ.

В табл. 2. приведены исходные данные для расчетов стандартной энтропии для соединений в системе Cr-Si. Анализ имеющейся информации показывает, что в рассматриваемой системе существует три области твердых растворов.

Таблица 2

Молярная энтропия силицидов хрома при стандартных условиях

№	Вещество	Структура	s, [2,3, 10, 11]	^8ут УР-(8)	AS.1	AS.1, ур. (12, 14, 16)	S, УР-(7)
	1	2	3	4	5	6	7
1	Si	ГЦК-4 (алмаз)	18,859±0,034	13,865
2	Cr	ОЦК-2 (a-Fe)	23,604±0,209	16,426	0,13931
3	Cr3Si CrSi о.ззззз	ку бич.-4 (Cr3Si)	95,814±1,464 31,938	17,114	0,06746	0,06733±0,00014	95,902±0,089 31,968±0,030
4	Cr2Si CrSi05	кубич.-4 (CaF2)		17,420		0,05998	68,181 34,091
5	Cr5Si3 CrSi06	тетрагон. (W5Si3)	177,402±3,138 35,480	17,593	0,05591	0,05550	178,056 35,611
6	Cr4Si3 CrSio 75	тетраг.		17,840		0,04877	153,374 38,344
7	CrSi	кубич.-4 (FeSi)	45,020±0,837	18,221	0,03732	0,03744±0,00012	44,932±0,085
8	Cr3Si4 CrSi 1.33333	куб.-8 (MgAl2O4)		18,681		0,03404	144,180 48,060
9	Cr2Si3 CrSii 5	ГПУ-8 (Мп2О3)		18,893		0,03240	99,520 49,760
10	CrSi2	ГПУ-6 (a-SiO2)	55,647±1,046	19,471	0,02764	0,02747	55,870

OTP-1: Cr - CnSi (x = 0HL33333). KO - Cr

В этой OTP по мере внедрения кремния в кристаллическую решетку металла происходит переход от структуры ОЦК-2 (Сг) к кубической структуре (Cr3Si). Вероятно, это вещество находится на границе между областями твердых растворов. Для

для кубической 6куб_2 = Объемная структур-8

ная постоянная ОТР-1:

Кх =*оцк-2 '^6.-2 ^кч           •—^•4 = 0,52269

12(V2—II 5

(координационное число ккч = 4).

Ур. (9) принимает вид:

AS7(CrSix) = AS-‘(Cr)-

K1[x„AS6,(Si)+AS,„(Cr)J

После подстановки ур. (10) окончательно примет вид:

AS7(CrSi,) = 0,13931-

X

- 0,52269 [0,33333 ■ 4,994 + 7,178] ’

AS;1 (CrSi,) = 0,13931 - 0,21636х .        (I2)

ОТР-2: CnSi - CrSi U = 033333-1,0). КО - CnSi

Во второй области твердых растворов переходу от кубической структуры, содержащей два атома в элементарной ячейке ( к^ __г = ^Е), к куби-

„                         - Vs.

ческой с четырьмя атомами в ячейке ( к^₅_₄ = — ) отвечает объемная структурная постоянная

^2 ⁼ ^куб -2 ’ ^куб -4 ‘ ^ккч ~~"    Т" • 4 = 1,1²500

о 4

(координационное число ккч = 4).

В качестве КО используем Cr3Si, тогда расчетное ур. (9) примет вид:

AS;,(CrSi,) = AS;1(CrSiO-33333)-

__*- °>³³³³³ __________ ₍₁₃)

K2[x,MjSi) + zV?^CrSi„^^

После подстановки численных величин уравнение (13) преобразуется к виду:

AS’1 (CrSi,) = 0,06746

__ х-0,33333

1,12500 [1,0-4,994+ 14,824]’

AS;1 (CrSi,) = 0,08241 - 0,04485х.       (14)

OTP-3: CrSi-CrSi, (х = 1 .0-2.0), KO-CrSi

В третьей области твердых растворов наблюдается переход от кубической структуры, содержа щей в элементарной ячейке 4 атома (кщ5 _4 = —— ),

7з -1

к структуре ГПУ (кгт_6 =-----) отвечает объ- емная структурная постоянная

^3 = ^6-4 ^щу-6 -Ккч =             = 2,76074

3     6

(координационное число кКч = 6).

В рассматриваемой ОТР в качестве кристаллообразующего выбран силицид хрома CrSi, тогда основное уравнение модели (9) примет вид:

as;¹ (CrSi,) = as;¹ (crsi) -

--х~1,0----------- / J 53

K3[x„AS^Si) + AS,„(CrSi)]'

После подстановки численных величин уравнение (15) преобразуется в:

AS’1 (CrSi,) = 0,03732

__ х-1,0 _________

2,76074 [2, О'4,994+ 26,799] ’

AS’1 (CrSi,) = 0,04717 - 0,00985х.       (16)

Вычисленные значения М7' и S представлены на рис. 2. Результаты расчетов согласуются с

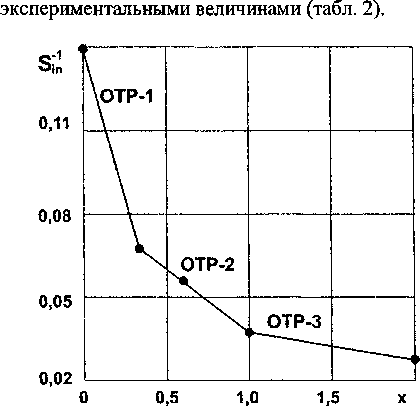
Рис. 2. Зависимость обратной энтропии взаимодействия силицидов хрома (CrSi,) от состава (• - эксперимент, _ - расчет)

Совместное решение ур. (12) и (14), (14) и (16) подтверждает правильность выбора границ между ОТР: х1_2 = 0,33176, х2.3 = 1,00686.

СТАНДАРТНАЯ ЭНТАЛЬПИЯ ОБРАЗОВАНИЯ

Наряду с теплоемкостью и энтропией в технической и химической термодинамике важнейшими характеристиками являются энтальпия и энергия Гиббса. В основу разработанной модели расчета Ду 7/2д8 (МеА,) положены универсальные правила линейной аппроксимации [16], предло- женные автором для проверки известных, определения неизвестных термических характеристик и их внутреннего согласования.

• 1.    Согласно предлагаемой модели [18, 19] стандартная энтальпия образования А^Я^ (МеА_х) выражается как удельная величина h (удельная энтальпия):

• 2.    Зависимость h от состава в рамках одной ОТР можно описать линейным уравнением вида:

И = ^{f 298} . (17)

Sz

Коэффициент Sz равен сумме ядерных зарядов z (порядковых номеров элементов) с учетом состава соединения.

h = a_h+K_nx. (18)

Графически эта зависимость имеет вид ломаной прямой. Координаты точек перелома отвечают составам границ между областями твердых растворов. Так как для каждой ОТР объемная структурная постоянная К„ имеет свое численное значение, определяемое сочетанием структурных констант веществ на границах ОТР, то координаты самих границ определяются совместным решением соответствующих уравнений (18) для соседних областей.

В табл. 3 приведены справочные значения стандартных энтальпий образования для четырех силицидов. Информация, содержащаяся в табл. 3, а также анализ характера зависимости S^¹ (х) показывают, что для исследуемой системы диаграмма h - х так же должна содержать три ОТР с теми же границами или близкими к ним [17, 18].

ОТР-1: Cr-Cr₂Si (х = 0-0,33333), КО-Сг

В этой ОТР по мере внедрения кремния происходит переход от структуры ОЦК (Сг) к кубической структуре (Cr3Si). Для ОЦК структурная константа ^оцк-2 = “ ’ А™ кубической - £ку6 _4 = |^ , координационное число кКч = 6. Объемная структурная постоянная ОТР-1:

Кх = ^оцк ' ^куб. ■ Ккч = 2 ^ ■ |^ ■ 6 = 4,77297 .

По определению первая область начинается с х = 0, следовательно, основное уравнение модели расчета стандартной энтальпии образования (ур. (18)) приводится к более простому виду:

(CrSiv) = 4,77297х (19)

OTP-2: CnSi - Cr2Si2 (х = 0,33333+0,6). КО - Cr,Sh

В этой области в качестве КО используем Cr5Si3. При переходе от кубической структуры, содержащей четыре атома в элементарной ячейке

3 /з                          л/3

К ГПУ ^у-^^

объемная

структурная постоянная второй области

^2 ⁼ ^куб-4 ‘ ^ГПУ-4 ' ^ккч ⁼ ^^" “^ "4 = 1,59099 (координационное число ккч ⁼ 4).

• Ур . (18) окончательно принимает вид:

^(CrSix) = l, 06066 + 1,59099х           (20)

Результаты расчетов по ур. (19) и (20) представлены в табл. 3 и на рис. 3. Их совместное позволяет определить границу между областями ОТР-1 и ОТР-2: х,_, = 0,33333, что точно отвечает составу CrSio, ззззз (Cr₃Si).

Таблица 3

Стандартная энтальпия образования силицидов хрома CrSi,

№	Вещество	Структура	-А^Я, [1-3, 10, 12]	z(CrSzx)	^,2,3	^,2,3 ’ yp. (19)-(21)	-АуЯ, УР-(17)
	1	2	3	4	5	6	7
1	Сг	ОЦК (a-Fe)	0	24,0	0	0	0
2	Cr3Si CrS 1о,ззззз	куб.-2 (CrSi3)	138,072+6,276 46,024	28,66667	1,60549	1,59099	136,824 45,608
3	Cr2Si CrSio 5	куб.-4 (CaF2)	-	31,0		1,85616	115,082 57,541
4	Cr5Si3 CrSio,e	ГПУ-4 (W5Si3)	326,352+6,092 65,270	32,4	2,01451	2,01525	326,470 65,294
5	Cr4Si3 CrSio,75	куб.-4 (Th3P4)	-	34,5		1,92339	265,428 66,357
6	CrSi	куб.-4 (FeSi)	71,128+6,276	38	1,87179	1,77030	67,271
7	Cr3Si4 CrSij,33333	куб.-8 (MgAl2O4)	-	42,66667		1,56618	200,472 66,824
8	Cr2Si3 CrSi, 5	ГПУ-2 (NiAs)	-	45		1,46412	131,770 65,885
9	CrSi2	ГПУ-3 (CrSi2)	59,831+4,184	52	1,15060	1,15793	60,212

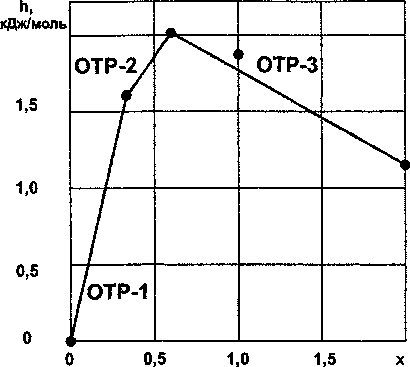
Рис. 3. Зависимость стандартной удельной энтальпии образования силицидов хрома (CrSix) от состава (• - эксперимент, — - расчет)

OTP-3: Cr5Sh - CrSi, (х = 0,6-2.0)

При переходе от структуры Cr5Si3 (^П]У..4

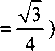
к структуре, в которой кристаллизуется соединение CrSi2 (^Гпу-8 = “^) объемная структурная постоянная для третьей области

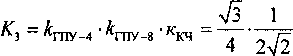
(координационное число ккч = 4).

Ур. (18) для третьей области окончательно принимает вид:

^(CrSi,) = 2,38267-0,61237x.        (21)

Результаты расчетов по ур. (21) также приведены в табл. 3 и на рис. 3. На рисунке 3 привлекает внимание явное «выпадение» из зависимости силицида CrSi, однако расчетная величина АН°98 (CrSi) не выходит за границы доверительного интервала справочного значения.

Решая совместно ур. (20) и (21), определим границу между ОТР-2 и ОТР-3: х2_3 = 0,599997, что практически отвечает составу граничного соединения - силицида Cr5Si3 (CrSi06).

СТАНДАРТНАЯ ЭНЕРГИЯ ГИББСА

ОБРАЗОВАНИЯ

Энергия Гиббса (свободная энергия) AG является одной из важнейших термодинамических характеристик. Особая роль ей отводится в химической термодинамике, так как величина и знак AG позволяют судить о состоянии системы - о ее положении относительно равновесия. Расчет AyG проводился по уравнению Гиббса. Применительно к стандартным условиям образования сложного вещества уравнение выглядит:

ЬД^Н^Д.     (21)

Для определения энтропии образования вещества использовали свойства Р-потенциала [19], что позволило согласовать величины Б_уН и A_yG соединений:

Р = AyS” - 5°,(22)

P(Me^Az) = yP(Me) + zP(A) =

= -yS(Me)-rf(A).(23)

Очевидно, что удельная энергия Гиббса g g = -^-(24)

подобно удельной энтальпии А, образует такие же

Таблица 4

Стандартные энергии Гиббса образования Д,^д силицидов хрома CrSi,

№	Вещество	A f’O ^/^298 > [2, 3,12]	° 298 ’ (табл. 2)	-P, yp.(23)	A V0 ^/^298 yp. (22)	A /7° 298 ’ (табл. 3)	g, УР- (24)	A yp. (21)
	1	2	3	4	5	6	7	8
1	Ст	0	23,604±0,209	23,604	0	0	0	0
2	Cr3Si Сг81о.3зззз	-137,134	95,991	-89,671	6,320	-136,824	1,6129	-138,707
3	Cr2Si CrSio,5	-	68,182	-66,067	2,115	-115,082	1,8663	-115,712
4	Cr5Si3 CrSio.6	-328,662	178,055	-174,597	3,458	-326,47	2,0216	-327,500
5	Cr4Si3 CrSio.75		153,376	-150,993	2,383	-265,428	1,9285	-266,138
6	CrSi	-71,889	44,847	-42,463	2,384	-67,271	1,7890	-67,981
7	Cr3Si4 CrSii ззззз	-	144,18	-146,248	-2,068	200,472	1,5614	-199,856
8	Cr2Si3 CrSiL5	-	99,52	-103,785	-4,265	131,77	1,4500	-130,499
9	CrSi2	-58,734	55,87	-61,322	-5,452	60,212	1,1267	-58,587

области твердых растворов. Зависимости h(x) и ES^ (х) внутри ОТР являются линейными функциями состава, следовательно, и зависимость g(x) должна иметь аналогичный линейный характер:

g = ф + К„х. (25)

Координаты границы между областями твердых растворов определяются совместным решением соответствующих уравнений (25) для сопряженных областей. В точках, отвечающих составам границ, наблюдаются излом g = /(х).

Результаты расчетов /’-потенциала и энтропий образования силицидов хрома приведены в табл. 4. По уравнению (21) с использованием полученных ранее S)₉₈ и ЕДЗ^ (табл. 2, 3) рассчитаны ^_/G“_9a силицидов хрома, также представленные в табл. 4.

В табл. 4 приведены значения удельной энергии Гиббса g, а на рис. 4 графически представлена ее зависимость от состава. Определение аналитического вида зависимостей g(x) для каждой из трех выделенных ОТР, позволяет рассчитать E^G^ для любых соединений, лежащих по составу в этой области.

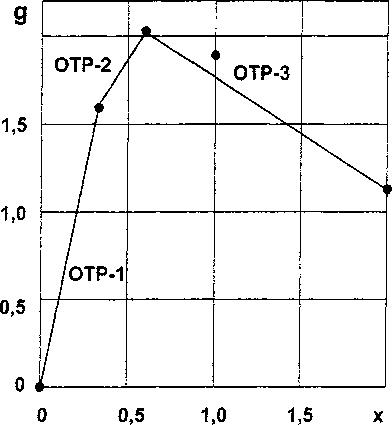
Рис. 4. Зависимость стандартной удельной энергии Гиббса образования от состава силицидов хрома (CrSi,) (• - эксперимент, — - расчет)

Выводы

• 1.    Разработаны математические модели расчета молярных теплоемкости, энтропии, энтальпии образования и энергии Гиббса образования при стандартной температуре для бинарных соединений, в которых оба компонента при стандартных условиях находятся в кристаллическом состоянии.

• 2.    Корректность разработанных математических моделей расчета подтверждена согласием с имеющимися справочными данными по кристаллическим силицидам хрома.

• [         3. Использование уравнений моделей позво

ляет рассчитывать значения термодинамических функций для бинарных соединений произвольного состава при стандартной температуре.