Термокинетический анализ параметров динамической сверхпластичности

The problem of the determination of the syn phase transition development particularities observed in condition dynamic superplasticity aluminum alloy, research the functions specific heat with use. Within the framework developed modelling representations with use of the equation Focker-Plank mechanisms to deformation typical for superplasticity and border metastability state are analysed. It is shown that under superplasticity the main mechanism is grain-boundary sliding, but in metastability state diffusive processes are added. The influence of the specified processes outside of conditions superplasticity becomes prevailling.

Задача установления особенностей развития размытых фазовых переходов, наблюдаемых в условиях динамической сверхпластичности алюминиевых сплавов, решается с использованием функции удельной теплоемкости. В рамках разработанных модельных представлений с привлечением уравнения Фоккера – Планка проанализированы механизмы деформации, характерные для сверхпластичности и пограничных метаста-бильных состояний. Показано, что при сверхпластичности основным является механизм зернограничного проскальзывания, а в метастабильных состояниях добавляются диффузионные процессы. Влияние указанных процессов вне условий сверхпластичности становится превалирующим.

В рамках модельных представлений [ 1,2 ] , пригодных для описания закономерностей высокотемпературной деформации в широких скоростных диапазонах, включая интервалы сверхпластичности, промышленных алюминиевых сплавов, получено [ 3 ] явное выражение для функции удельной теплоемкости

А C/k = a( с ) п 2 + b( с ) п , (1)

где к - постоянная Больцмана, п = Д" — 1 — параметр порядка, £ - скорость деформации, dв do*!*°

^{a( с} ) = ^{- (} ^^v ) — + 2 Р—— d с       d с

- ( с + V)²

в ded    +1 d4-2Р2ГdY dс dс    2 dс2     ( dс J

_ d ² In ° *

+ в---T- dс1

d в d In ° * ⁺ d [ d с

*

b (0 = -2(C + v)       + (с + v)2 в d с

+ ( с + V )² в

² d In ст *

I d с J

,

d g d ln£ + кс + v ) ! в 2 d с   d с

- ( с + V )²

d ² In ° * d с ²

² d In °

I dс J

* \ 2

- +

+

причем β есть решение уравнения

(1 -β ) ^α

1 +α µ- 1 1 + µ (2 ξ - 1)²

= 1 -             ln               ;

2 α µ 1 +µ

а v = θ _c ^н / ∆θ _с , где ∆θ _с = θ ^в _с - θ _с ^н – температурный диапазон сверхпластичности;

ξ=

θ-θ с^н θ ^вс -θ с^н

– нормированная температура ; θ – абсолютная температура; θ _c ^н , θ ^в _c – ниж-

няя и верхняя границы термического диапазона сверхпластичности; α , µ – постоянные материала; о * , £ * - внутренние альтернативные параметры состояния;

dlnσ∗

= A0exp(β-s);

dξ dln £ *    ..

= A ₀ exp( β- s) β .

dξ

В соответствии с [1,2] при β >  0( ξ ∉ ]1,0[) изменений структурного характера в деформируемом материале не происходит. Условие β <  0(ξ ∈ ]1,0[) отвечает структурно неустойчивому состоянию среды. Если β = 0 , то имеют место переходные процессы.

На параметр порядка η накладываются следующие ограничения:

• ♦    на область структурных превращений

  - ( -β /m ₀ ) ^{1 / 2} ≤η≤ ( -β /m ₀ ) ^{1 / 2}                          (7)

• ♦    на диапазон развития сверхпластичности

  - ( -β /3 m 0 ) ^1/2 ≤η≤ ( -β /3 m 0 ) ^1/2.                           (8)

Проанализируем информацию, которая следует из найденного приращения удельной теплоемкости в форме (1).

Иными словами, с привлечением методов неравновесной статистической механики оценим вклад различных механизмов деформации в температурно–скоростные режимы структурного фазового перехода – динамическую рекристаллизацию, соответствующую сверхпластичности.

Соотношения (1) – (4) устанавливают зависимость ∆ C от температуры и скорости деформации. Обратимся теперь к кинематике сверхпластического течения, т.е. ∆ C = ∆ C ( η , t ). Положим, что эта функция монотонно эволюционизирует от любого начального распределения плотности вероятности к равновесному состоянию.

Указанная эволюция описывается, как известно, уравнением Фоккера–Планка [4].

^{∂∆ C ( η , t )} =- ^∂ [ R ( η ) ∆ C ( η , t ) ] + ^{1 ∂ 2} [ Q ( η ) ∆ C ( η , t ) ] .               (9)

∂ t       ∂η                 2 ∂η ²

Здесь функция Q ( η ) – коэффициент диффузии, а функция R ( η ) называется коэффициентом «дрейфа» [5] и описывает систематическое торможение.

Для сверхпластичности примем соответствующей стационарную форму уравнения (9). При этом на функцию R ( η ) будем возлагать ответственность за реализацию механизма зернограничного проскальзывания. При сверхпластичности формы массоперено-са, конкурирующие с указанным механизмом, затормаживаются и коэффициент диффузии можно принять постоянным Q ( η ) = Q _0.

С учетом изложенного уравнение (9) перепишется следующим образом:

d- [ R ( п ) Д c ( n ) ] - 1 Q 0 ^{d 2} ^ C 2 ^{( n )} = 0.                      (10)

d n              2      d n

Подставив (1) в (10), после несложных преобразований получаем линейное дифференциальное уравнение dR (n) dn

+

2 a n + b a n ² + b n

R ⁽ n ) =

aQ ₀ a n ² + b n

Решение уравнения (11) будем искать при условии, утверждающем, что на границе сверхпластичности и метастабильной зоны имеем

R( n ) „,(-, / 3 m 0 !' ² = R 0 .                                    (12)

Если учесть, что при переходе от метастабильного состояния к области структурной неустойчивости ( n = ± ( -P / m оУ/2 ) функция R ( n ), отвечающая за эффект зернограничного проскальзывания, обращается в нуль, то интеграл уравнения (11) будет иметь вид

a

V

³ m 0 )

+ b

V

в

1 / 2

³ m 0 )

V

1 / 2

в)

m 0 )

^^^^^^^в

n

[ a n 2 + b n

1 / 2

в)

V

m 0 )

ш ' ²

V ³ m 0 )

R( n )

R 0

при 0 < n ^ ( -P ' 3 m ₀ ) 1 ' 2 ,

C

a

V

3 m ₀ )

C - b

V

P

1 / 2

1 / 2

P)

-

3 m ₀ )

V

^m 0 )

n

[ a n 2 + b n

C--T ' ² +С-Л) ¹²

V m 0 )    V 3 m 0 )

при - ( -P ' 3 m ₀ ) ^{1 / 2} < n <  0 •

На рис.1. приведены график функции R( n ) , рассчитанный для значений температуры 6 = 753 K (в = - 0,0335354, m ₀ = 0,333), принадлежащих сплаву АМг5 в условиях

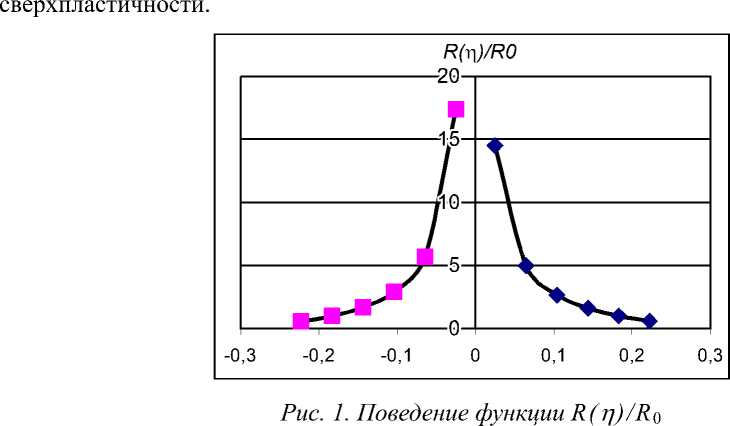
Из графика видно, что к середине скоростного диапазона сверхпластичности ( р >  0 ) все механизмы деформации, кроме проскальзывания по границам зерен, становятся несущественным ( R (0) ^ да ).

Вне кинематического диапазона сверхпластичности R ( п ) = 0 и активизируются традиционные формы массопереноса.

Уравнение (9) при этом перепишется так:

d^ [ Q ( П ) А C ( п ) ] = 0. d п

Принимая во внимание (1), уравнение (14) преобразуется в дифференциальное уравнение второго порядка d2Q(п)      /  7Q(п)     Z X п

, 2  + 2ф, (п)       + Ф2 (п)Q(п) = 0, dп

. .    2 а п + b         , .

где Ф1 (п)=—2—; Ф2 (п)=—2• а п + b п          а п + b п

Уравнение (15) подстановкой U ( п ) = Q ( п )exp [ J ф ₁( п ) d п ] сводится к следующему уравнению и "( п ) = 0, после интегрирования которого окончательно имеем

^Q ( п ) =

С 1 п + C ₂ а п ² + b п

где С 1 , С 2 - постоянные интегрирования.

Уравнением (14) предполагается, что функция R ( п ) вне диапазона сверхпластич-

ности п £

состоянии

[ - ( -в / m ₀ ) ^1/2; ( -в / m ₀ ) ^1/2 ] обращается в нуль. Полагая, что в метастабильном ( п е [ ± ( -в /3 m ₀ ) ^1/2; ± ( -в / m ₀ )^Ш ] ) известные формы массопереноса сосущест-

вуют с зернограничным проскальзыванием, следовательно, граничные условия можно записать так:

^{Q (} п ) _п=± ( -в /3 m 0 Г

. dQ ( п ) = ^Q 0 ; .

d п

I                  1/2

| п=± ( -в /3 m 0 )

= 0.

С учетом условий (17) для коэффициента диффузии получаем

2 а

в

Л1/2

V

Зти ³ m 0 у

+ b п- а

в

\

V

Зги ³ m 0 у

а п ² - b п

Q ( п ) Q 0

при - ( -в /3 m о ) ^1/2 < п ^ 0,

2 а

V

в

1/2

^{3 m} 0 У

+ b

п- ^а

V

в )

^{3 m} 0 У

ар2 + b п при 0 < п < (- в / 3m0)1/2.

На рис.2. представлен график функции

Q ( η )

Q 0

~ η , построенный для упоминавше-

гося выше сплава АМг5 при ^β = - 0,107. Из графика видно, что при приближении ско- m ₀

рости к режимам сверхпластичности влияние диффузионных процессов убывает, причем коэффициент диффузии стремится к значению Q 0 , соответствующему сверхпластичности.

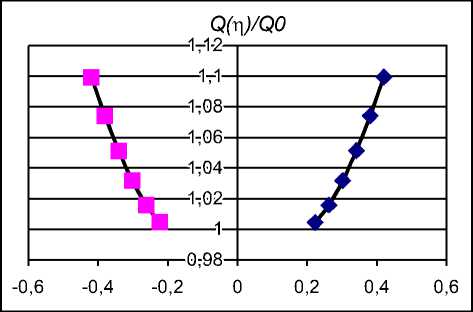
Рис. 2. Зависимость коэффициента диффузии от параметра порядка

Укажем, что качественное поведение функций R ( η ), Q ( η ) не изменится для всей группы алюминиевых сплавов.