Термомеханическое поведение полимерных композитов и его расчет с помощью конечно-элементного моделирования

Полимерные композиты представляют собой эффективный материал для создания газоходов и дымовых труб благодаря оптимальному сочетанию их прочности и малого веса, устойчивости к агрессивным воздействиям окружающей среды [1], [2], а также возможности модифицирования свойств за счет изменения структуры материала [3]. Важнейшим преимуществом полимерных композитов является их высокая коррозионная стойкость, которая значительно превосходит показатели традиционных материалов, таких как сталь или железобетон, склонных к быстрому разрушению под воздействием коррозии [4].

На данный момент в таких конструкциях несущая способность не используется в полной мере из-за ограниченного понимания его поведения при длительном термомеханическом воздействии, а также недостаточного отражения этих аспектов в нормативных документах (в отличие от традиционных материалов). Обычно внешние механические нагрузки воспринимаются поддерживающими элементами, такими как решетчатые башни, оттяжки или другие трубы, например при реконструкции и монтаже газоотводящих стволов внутри существующих сооружений. Однако существуют примеры успешного применения несущих стеклопластиковых труб. Так, например, была возведена 52-метровая отдельно стоящая труба на Zadorin, A.; Korolev, A.; Mishnev, M.

Thermomechanical behavior of polymer composites and its calculation with finite element modeling;

сахароперерабатывающем заводе в США в 1984 году [5]. Это свидетельствует о перспективах улучшения эффективности использования композитов в строительной отрасли посредством устранения информационных пробелов и обновления соответствующих норм. Разработка несущих композитных труб и газоходов может привести к снижению затрат на строительство за счет исключения необходимости в поддерживающих конструкциях или их удешевлении, а также к сокращению расходов на обслуживание, поскольку металлические элементы поддерживающих башен, склонны к коррозии.

Применение материала в условиях эксплуатации дымовых труб и газоотводящих трактов требует решения ряда задач, включая изучение влияния температуры на физико-механические свойства, процессов температурного старения, реологических характеристик материала (вязкоупругое поведение), возникновение температурных напряжений и их возможная аккумуляция.

Вопросы жесткости и прочности при нормальных и повышенных температурах в силу того, что эта тема является актуальной для многих областей применения, изучались довольно обширно. В [6] приводятся кривые напряжений-деформаций для ряда композитов с разной гибридизацией при температурах 25-100°C, а также кривые падения модуля упругости при действии температуры. В [7] проведены испытания трехслойных сэндвичевых систем, состоящих из двух стеклопластиковых обшивок и изолирующего ядра из фенольной пены. Это исследование ценно для нашей области, т.к. стеклопластиковые трубы изготавливаются в том числе трех- или пятислойными. Однако в [7] нагрев производился равномерно с обеих сторон, а в дымовых трубах происходит неравномерное воздействие горячих отводимых газов и холодного наружного воздуха. С одной стороны, это приводит к дополнительным напряжениям от изгиба, а с другой, наружная обшивка остается холодной и дольше не теряет жесткость. В любом случае, анализ воздействия температур на НДС конструкций необходим. В наших предыдущих работах проводилось изучение свойств полимеров и композитов при нормальных и повышенных температурах: получены данные о жесткостных характеристиках [8], изучалась износостойкость материала [9], рассматривались вопросы прогнозирования свойств как полимеров [10], [11], так и композитов [12]. Кроме того, проводилось определение их коэффициента линейного термического расширения (КЛТР), его нелинейности и взаимосвязи с другими параметрами [8], [13].

Температурное старение материала также изучалось нами и другими исследователями. В [14] было установлено, что этот эффект зависит от значения температуры и может быть как положительным (вызывая эффект доотверждения), так и отрицательным (приводя к деградации материала). То есть, температурный режим конструкции оказывает прямое влияние на ее долговременные свойства. Также изучалось влияние старения на работу в разных условиях [15– 17]. Нами была проведена оценка влияния температурного выдерживания на жесткость и КЛТР материала и сделаны предположения о влиянии старения на внутреннюю макромолекулярную структуру [8], [18], [19].

Вопросы вязкоупругого поведения полимеров были исследованы многими учеными, и разработаны методы оценки этого явления, включая ускоренные испытания на основе температурно-временной аналогии [20]. Имеются данные о влиянии вязкоупругости на поведение материала при динамических и циклических нагрузках, а также о влиянии внутренней структуры и армирования [21], [22]. Подчеркивается важность учета вязкоупругих свойств материала [23]. Тем не менее, каждый раз возникает необходимость выбора подходящей модели вязкоупругого материала и определения её параметров для конкретного случая. В общем, методики тестирования на ползучесть хорошо проработаны, включая нормативные документы. Однако, учитывая особенности эксплуатации дымовых труб и газоходов, где присутствуют долговременные нагрузки, продолжительное тепловое воздействие, а также возможные циклические температурные и механические воздействия, необходима модель вязкоупругого материала, которая будет учитывать одновременные нелинейные изменения жесткости, коэффициента линейного термического расширения (КЛТР) и реологических параметров при нагревании. Одно из следствий вязкоупругой природы полимеров – возможность накопления деформаций и напряжений при циклических воздействиях. Их влияние может быть непредсказуемым, т.к. оно зависит одновременно от вязкоупругих свойств, температурных свойств и условий работы сооружения. Эти вопросы поднимались учеными ранее. Установлено [24], что циклические температурные воздействия приводят к снижению прочности и жесткости материала.

Таким образом, определение термомеханических и реологических свойств материала является актуальной темой, широко изучаемой по всему миру. Моделирование и определение механических и температурных свойств термореактивных полимеров и стеклопластиков на их основе были объектами многих исследований. Одним из направлений исследований является моделирование материала и расчет его характеристик различными способами. Можно выделить 2 основных подхода:

• 1)    Аналитическое моделирование с помощью функциональных моделей: начиная от классической модели вязкоупругого тела Кельвина-Фойгта [6], [25], [26], заканчивая моделями с релаксационным ядром и графическими методами прогнозирования деформаций [27], [28];

• 2)    структурное моделирование представлено в различных исследованиях, где структура была смоделирована с помощью компьютерных программ. Например, проектирование трехмерных молекулярных моделей в соответствии с определенными углами связей молекул полимера [29]–[32], молекулярно-динамическое проектирование молекулярной структуры и свойств полимера [33], [34], компьютерное моделирование многомасштабных гетерогенных структур наполненных полимеров и стеклопластиков на молекулярном и надмолекулярном уровне [35]–[37].

В недавних исследованиях моделирование сочетает функциональные и структурные многомасштабные методы [38] с термическими зависимостями механических свойств. Однако прогнозирование эксплуатационных свойств отвержденных полимеров и стеклопластиков остается актуальной научной проблемой, особенно для структурных моделей. Они требуют определения основных элементов, их конфигурации и взаимного расположения в модели, а также механических и тепловых свойств этих элементов.

Использование КЭ-моделирования может позволить легко и быстро прогнозировать эксплуатационные свойства полимеров и стеклопластиков. По этой причине к нему существует постоянный интерес [39], [40].

Целью данного исследования в рамках гранта РНФ №23-29-00425 была разработка альтернативной расчетной модели армированного стекловолокном полимера (стеклопластика), основанной на ранее предложенной КЭ-модели чистого полимера и позволяющей прогнозировать термомеханические характеристики композита, температурные напряжения, обеспечивать корректное определение напряженно-деформированного состояния рассчитываемого элемента, сопоставимое с другими стандартными способами моделирования.

Для этого были поставлены следующие задачи:

• -    Испытать образцы стеклопластиков и связующего для определения их термомеханических характеристик при различных температурах;

• -    Разработать КЭ-модель стеклопластика на основе ранее предложенной модели полимера;

• -    Сравнить работу модели с экспериментальными данными и с КЭ-расчетом по стандартной схеме;

• -    Сделать выводы о применимости модели и определить направления по ее усовершенствованию.

• 2    Materials and Methods

Состав полимерного композита:

• -    Эпоксидная смола KER 828 (аналог ЭД20), Производитель: KUMHO P&B Chemicals;

• -    Изометилтетрагидрофталевый ангидрид (ИЗОМТГФА) (отвердитель для эпоксидной смолы). Производитель: ASAMBLY Chemicals company Ltd., Nanjing, China;

• -    Алкофен (ускоритель отверждения эпоксидных смол). Производитель: АО "Эпитал", Москва, Российская Федерация;

• -    Стеклоткань Т23 [41].

Испытания проводились на испытательной машине Tinius Olsen H100KU (Tinius Olsen Ltd., Суррей, Англия) в специально изготовленной камере, оснащенной нагревательными элементами и термостатом (рис. 1).

Рис. 1 – Испытательная камера

Fig. 1 – Testing chamber

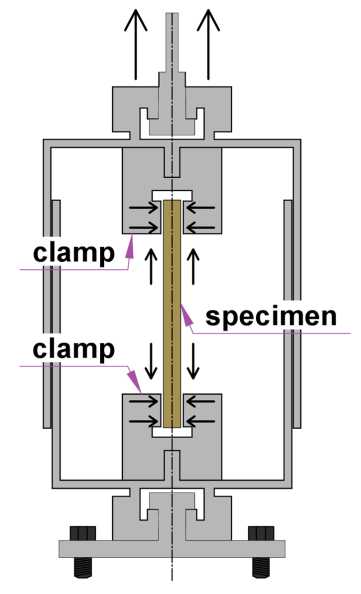
Методика испытаний на растяжение аналогична ранее подробно описанной авторами [42]. В испытательной камере были определены модуль упругости и прочность чистого связующего и композита при нормальной и повышенных температурах. Коэффициент линейного температурного расширения (КЛТР) был определен в предыдущих исследованиях [8], а также определялся в данной камере путем освобождения верхнего зажима и замера удлинения образца при нагреве.

Ранее авторами была представлена конечноэлементная (КЭ) модель отвержденного полимера [43], позволяющая определять модуль упругости и прочность материала при нормальной и повышенных температурах. В продолжение это работы предлагается модель армированного полимера (стеклопластика).

КЭ-модель стеклопластика была основана на КЭ-модели отвержденного полимера. Как отмечалось ранее, структура модели самоподобна, и мы не строим ее, используя реальный размер и количество связей. Модель полимера представляет собой приближение к реальной хаотической структуре, усредненное на основе условия соответствия плотности связей на единицу объема и соответствия свойств материала. Используя тот же принцип, была разработана модель стеклопластика путем введения стержней, имитирующих стекловолокно. Количество этих элементов и их толщина определялись по соответствующей действительности относительной площади (площади волокон, отнесенной к площади сечения). Эта величина была определена авторами ранее с помощью микрофотографий сечения композита [12]. Стержни из стекловолокна были размещены максимально равномерно по площади сечения. В целом, модель аналогична представленной ранее [43]. 3D вид модели композита приведен на рис. 2.

Характеристики стекловолокна: стеклоткань T23 изготовлена из E-glass со средним модулем упругости 80–81 ГПа и прочностью 3000–3500 МПа. В текущей модели мы использовали модуль упругости 80 ГПа и прочность 3300 МПа.

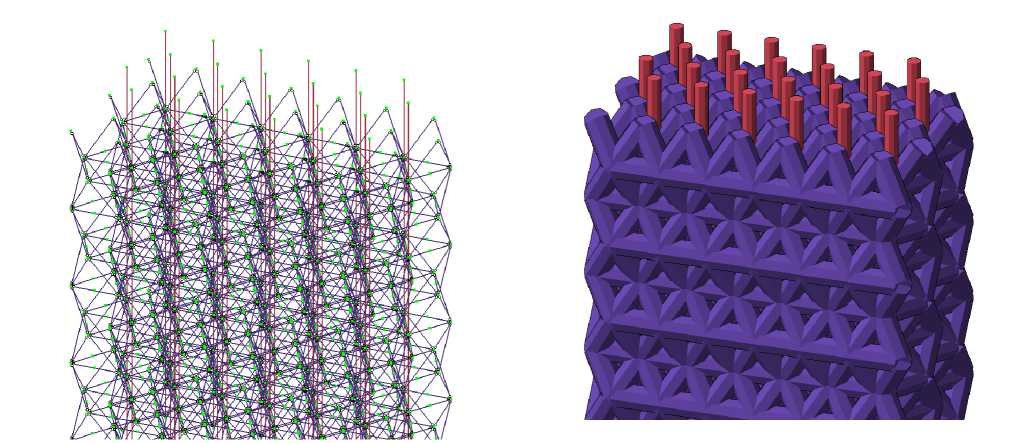
Рис. 2 – Общий вид фрагмента модели и 3D – вид поперечного сечения КЭ-модели композита Fig. 2 – General view of the fragment of the model and 3D view of the cross-section

Ранее авторами были получены значения КЛТР при различных температурах для полимеров и композитов [8]. Однако при одном и том же связующем свойства материала могут меняться при использовании различных стеклотканей. Чтобы получить возможность рассчитывать строительные конструкции и сооружения, в т.ч. с учетом температурных напряжений и их накопления, например, в дымовых трубах; вести вариантное проектирование; подбирать оптимальное армирование, необходима аналитическая или КЭ модель, позволяющая менять параметры армирования и получать адекватный результат. Имеющаяся на данный момент КЭ-модель позволяет это делать, но без учета температур. Поэтому дальнейшим шагом было внедрение температурного фактора в модель.

Программа позволяет прикладывать температурные нагрузки на стержни, задавая температуру нагрева и КЛТР. Как известно [8], модуль упругости и КЛТР как полимерной матрицы, так и композитов меняется при нагреве, причем нелинейно. Поэтому КЛТР и E определялись отдельно для заданных значений температур путем приложения минимальной температуры нагрева dt = 1⁰C и задания параметров модели, соответствующих данной температуре. Таким образом, в КЭ-модели композита на полимерные связи и стекловолокно прикладывалась температурная нагрузка, ранее полученный КЛТР для полимера и известный КЛТР стекловолокна. Было установлено, что оптимальным оказывается значение КЛТР связей на 10% ниже соответствующего полимера, что связано с тем, что сами по себе связи более жесткие и прочные, чем материал в целом. Далее определялся общий КЛТР полимерного или композитного образца и модуль упругости по следующему алгоритму (см. рис. 3):

• 1.    Один конец образца в модели освобождался от связей. Задавались свойства элементов, соответствующие расчетной температуре. На элементы прикладывался нагрев на 1 C . По полученному в результате расчета удлинению образца определялся его КЛТР, пользуясь известной зависимостью (1):

• 2.    Далее, зная КЛТР образца, его свободный конец в модели защемляли и прикладывали температуру аналогичным образом. Пользуясь другой известной зависимостью (2), определялся модуль упругости при данной температуре:

∆ L = α ⋅ L ⋅∆ T ,

где α - коэффициент линейного температурного расширения (КЛТР),

L - изначальная длина образца,

∆ T - изменение температуры.

σ = α ⋅∆ T ⋅ E ,                                  (2)

Где σ - нормальные напряжения от действия температуры (определялись делением суммарной продольной реакции опор образца на площадь сечения),

E - модуль упругости.

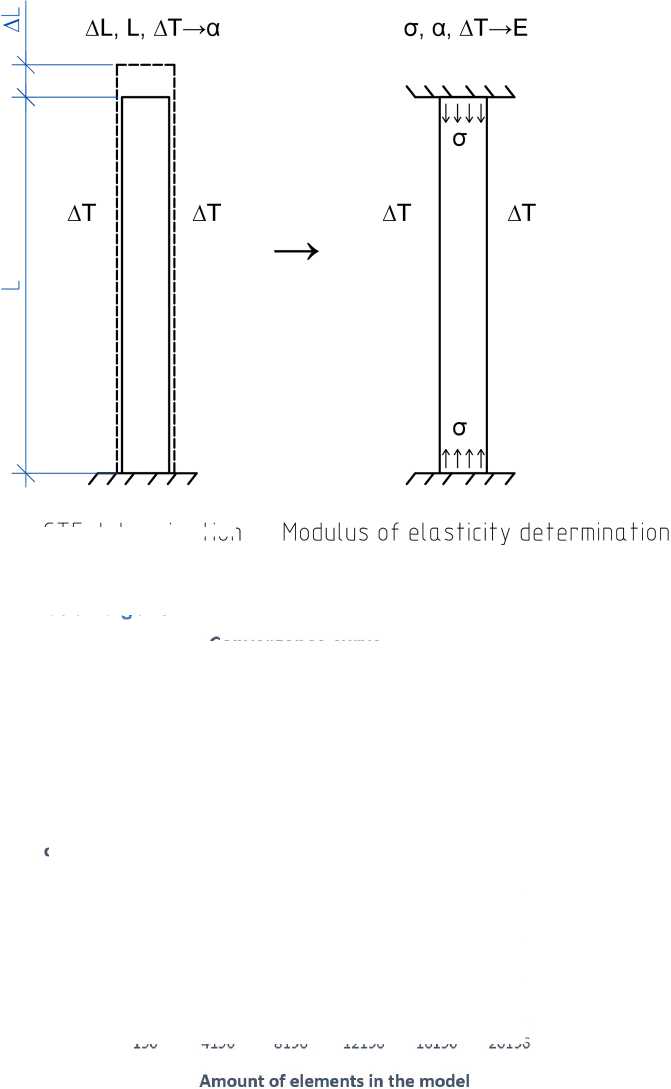
CTE determination

Рис. 3 – Алгоритм расчета КЭ-модели Fig. 3 – FE model’s calculation algorithm

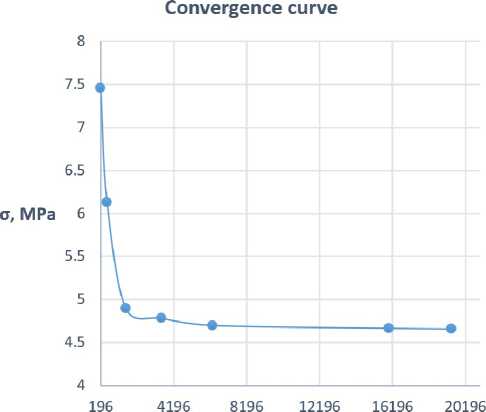
Рис. 4 – Кривая сходимости

• Fig. 4 – Convergence curve

  Как ранее было упомянуто, структура полимерной матрицы в модели самоподобна. Это свойство позволяет строить модель с любым количеством базовых ячеек на единицу объема. Оценка адекватности принятого масштаба была определена по стандартной кривой сходимости модели. За контролируемый параметр были приняты нормальные напряжения образца (как его суммарная реакция опоры, поделенная на площадь сечения). Ось абсцисс – число элементов в модели. На рис. 4 приводится кривая сходимости. Как видно из графика, при порядке элементов 10⁴ достигается сходимость. В итоговой расчетной модели был 19451 элемент.

3 Results and Discussion

Модель композита сразу показала высокую сходимость с имеющимися экспериментальными данными для подобного композита [8]. В таблице 1 приводится сравнение экспериментальных и полученных по модели данных.

Таблица 1. Модуль упругости композита

Table 1. Elastic modulus of the composite

Температура, oc	Экспериментальные данные		Рассчитанные по модели данные
	E, МПа	R, МПа	E, МПа	R, МПа
25O C	12000	160	13000	168

Однако изначально расчет при повышенных температурах не показал адекватных результатов. Исходя из того, что модуль упругости и прочность во всех случаях были завышенными и анализируя модель, было выдвинуто предположение, что это связано с тем, что в модели не учитывается ослабление совместной работы волокон и полимера. Была предпринята попытка условно учесть этот фактор. По аналогии с тем, как в модели полимера мы снижали толщину связей для моделирования их ослабления, в модели композита снижалась толщина волокон, т.е. суммарная продольная составляющая жесткости сечения снижалась.

Таким образом, моделировалось не полное вовлечение волокон в работу сечения, обусловленное снижением жесткости полимерной матрицы. Был введен коэффициент армирования, представляющий собой отношение расчетной площади армирования к полному нормальному значению. Значения коэффициента были аппроксимированы по известным экспериментальным значениям модуля упругости. Расчетные значения относительной площади армирования (отношение площади волокна в сечении к общей площади сечения) приводятся на графике на рисунке 5.

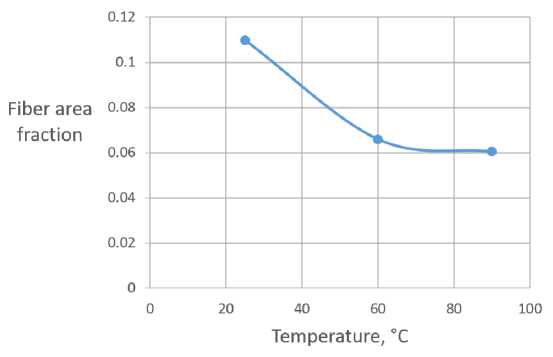
Рис. 5 – Доля площади волокна

Fig. 5 – Fiber area fraction

Таким образом, была получена возможность моделировать работу композита при любой температуре, что открыло нам возможности для перехода к температурным напряжениям и деформациям.

В усовершенствованной модели с помощью методики, описанной ранее, были получены значения модуля упругости и КЛТР полимера и стеклопластика при нормальной и повышенных температурах, и они имели хорошую сходимость с имеющимися экспериментальными данными. Полученные значения в сравнении с известными из предыдущих исследований [8] и испытаний приводятся в таблице 2.

Таблица 2. Результаты расчетов по модели и сравнение с экспериментальными данными Table 2. The results of calculations based on the model and comparison with experimental data

Температура, °C	Расчет по модели		Экспериментальные данные		Погрешность, %
	E, МПа	КЛТР, 1/ C	E, МПа	КЛТР, 1/ C	E, МПа	КЛТР, 1/ C
Чистое связующее

25 С	2780	22 ^ 10 -6	2700	21 ^ 10 —6	2.9	4.5
50 С	2390	25 ^ 10 -6	2300	24 ^ 10 —6	3.8	4
75 С	2213	27 ^ 10 -6	2100	26 ^ 10-6	5.1	3.7
100 С	1428	40 ^ 10 -6	1400	38 ^ 10-6	2	5
Стеклопластик
25 С	12745	8.91 - 10 -6	12000	9d0-6	5.8	1
50 С	9481	10.3 ^ 10 —6	9900	10d0-6	4.2	2.9
75 С	7975	11.3 ^ 10 —6	8360	11 •Ю-6	4.6	2.7
100 С	6743	12.7 ^ 10 —6	7300	12d0-6	7.6	5.5

Таким образом, модель позволяет прогнозировать термомеханические характеристики композита с высокой точностью, зная характеристики связующего и стеклоткани. Кроме того, из этого следует соответствие рассчитанного напряженно-деформированного состояния (НДС) композита действительности в целом. Для проверки этих выводов далее производится:

• 1.    Проверка модели для предсказания модуля упругости другого композита из другой партии.

• 2.    Сравнительный расчет защемленного элемента на температурное воздействие по предлагаемой структурной модели и по стандартным стержневой и оболочечной моделям.

На данный момент имеются данные о модуле упругости с другой партии образцов связующего и композита, используемых в другом исследовании, при нормальной температуре. Таким образом, задаваясь известными параметрами смолы (и перенося их в модель с помощью корреляционных зависимостей, полученных ранее [43]), проверим работоспособность модели на других данных:

Таблица 3. Результаты расчетов по модели и сравнение с экспериментальными данными другой партии образцов

Table 3. The results of calculations based on the model and comparison with experimental data

Температура, С	Расчет по модели	Экспериментальные данные	Погрешность, %
	E, МПа	E, МПа	E, МПа
Чистое связующее
30 С	3049	3000	1.6
Стеклопластик
30 С	11887	10783	9.3

Как видно из таблицы 3, модель также хорошо себя показывает на другом наборе данных. Таким образом, делается вывод о возможности применения модели для прогнозирования свойств полимерных композитов различных составов, исходя из свойств связующего и армирования. В перспективе это может позволить ускорить и удешевить проектирование стеклопластиковых конструкций, т.к. отпадает необходимость экспериментального определения характеристик каждого состава. В особенности это упрощает вариантное проектирование и позволяет подобрать оптимальный вариант, при необходимости проверив экспериментально только его.

Сравнительный расчет для подтверждения НДС образца проведен по следующим схемам (температура нагрева одинакова и равна 50^е С , во всех случаях стержень защемлен с обоих концов и в нем возникают температурные напряжения):

• 1.    Вышеописанный расчет по структурной модели;

• 2.    Расчет образца как защемленного стержня;

• 3.    Расчет образца как защемленной пластины.

Ниже приводятся изображения схем (рис. 6) и сравнение результатов (таблица 4):

Рис. 6 – Варианты расчетных моделей

Fig. 6 – Variants of calculation models

Таблица 4. Результаты расчетов по модели и сравнение с экспериментальными данными другой партии образцов

Table 4. The results of calculations based on the model and comparison with experimental data

Параметр	Структурная КЭ-модель	Стержневая модель	Оболочечная модель
σ, МПа	4.02	4.08	4.1
E, МПа	8035	8160	8218

Structural FE-Model

Rod model

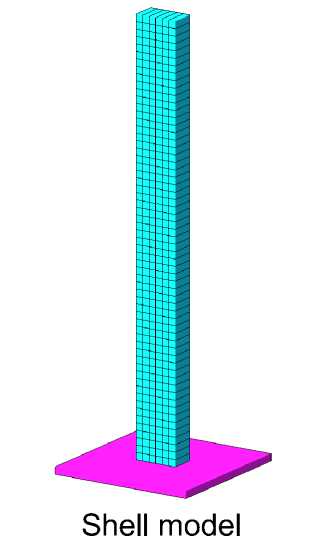
Таким образом, предлагаемая структурная модель имеет НДС, аналогичное стандартным схемам. При этом имея преимущество в виде возможности модифицирования свойств связующего и армирования по отдельности, изменяя и прогнозируя свойства композита в целом.

Из недостатков модели можно отметить условный учет неидеальной совместной работы волокна и полимера при нагреве, на данный момент учитываемый с помощью занижения расчетной площади волокна в сечении по корреляционной зависимости. Хоть на данный момент модель позволяет получать точный результат, эта зависимость может оказаться неверной при использовании другого связующего или типа армирования.

4 Conclusions

Для развития применения несущих и самонесущих стеклопластиковых труб одним из направлений исследований стало аналитическое и компьютерное моделирование работы полимеров как чистых, так и армированных стекловолокном. В качестве альтернативы стандартным аналитическим решениям, таким как, например, модель Кельвина-Фойгта и разрабатываемым производным из нее, в данной работе была предложена альтернативная структурная КЭ-модель полимера и композита. Эта модель позволила с высокой точностью определять модуль упругости и КЛТР композиционного материала по известным свойствам его составляющих. При этом эта же модель в целом показывает НДС, аналогичное стандартным решениям. Таким образом, она может применяться в том числе при расчетах и проектировании стеклопластиковых конструкций, за счет своих особенностей позволяя вести вариантное проектирование, подбирать оптимальный состав композита.

В данной статье:

• 1)    Выполнено экспериментальное исследование стеклопластика на эпоксидном связующем и самого связующего при различных температурах для определения его модуля упругости и КЛТР.

• 2)    На основе ранее выдвинутой КЭ-модели связующего, предложена КЭ-модель стеклопластика.

• 3)    Настроенная по экспериментальным данным и известным корреляционным зависимостям под конкретное связующее и армирование модель была использована для расчета КЛТР и модуля упругости композита; результаты сопоставлены с экспериментальным данными и оказались точными.

Zadorin, A.; Korolev, A.; Mishnev, M.

Thermomechanical behavior of polymer composites and its calculation with finite element modeling;

• 4)     Напряженно-деформированное состояние образца, определенное по предлагаемой

модели, было сопоставлено со стандартными стержневой и оболочечной моделями; результаты также были практически одинаковы.

В дальнейшей работе планируется более точное моделирование зоны контакта волокна и полимера и сдвиговых деформаций в матрице. Также в дальнейшей работе планируются испытания образцов других форм, более близких к интересующих нас оболочкам, например кольцо, и задание аналогичной формы нашей КЭ-модели, т.к. ее строение позволяет задать любую форму.

Таким образом, была разработана и проверена КЭ-модель стеклопластика, имитирующая его внутреннюю структуру. Данная модель позволяет:

• 1)    Прогнозировать свойства композита, основываясь на свойствах его составляющих: полимерного связующего и армирования;

• 2)    Прогнозировать температурные напряжения и деформации этого композита;

• 3)    Сократить стоимость и сроки проектирования стеклопластиковых конструкций за счет возможности виртуально проверить большое количество возможных составов, подобрать оптимальный, при необходимости проведя поверочные испытания только одного интересующего состава.

Предлагаемый способ расчета полимерных композитов является перспективной альтернативой традиционным аналитическим расчетам, в первую очередь за счет упрощения и доступности не только для ученых, но и для инженеров-проектировщиков.

• 5    Fundings

  Проект выполнен при поддержке Российского научного фонда, грант №23–29–00425 https://rscf.ru/project/23-29-00425/.

The work was funded by the Russian Science Foundation, grant №23–29–00425

• 6    Conflict of Interests

The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.