Терморезисторная сеть измерения температуры с небольшим количеством проводов

Наличие большого количества соединительных проводов усложняет реализацию измерительной системы на контролируемом изделии, особенно на борту космического аппарата. Поэтому образцы измерительных сетей с небольшим количеством проводов активно используются для температурного анализа исследуемых объектов в труднодоступных, экстремальных или агрессивных средах [1-7]. В таких сетях поступление всего одного измерения для анализа большого количества данных может компенсироваться динамической вариацией источника питания и последующей компьютерной обработкой данных [7].

В статье представлена измерительная сеть с тремя соединительными проводами и двумя источниками напряжения: постоянного тока и с пилообразным сигналом. В сети измеряется только ток в одном из проводов, а требуемые температуры (зависящие от текущих сопротивлений термисторов [8-10]) рассчитываются специальным компьютерным алгоритмом обработки имеющейся информации. Источник напряжения пилообразного сигнала создает различные режимы питания, которые приводят к переключению состояния сети за счет перехода части диодов из закрытого состояния в открытое. Грубо говоря, закрытые диоды трансформируют исходную сеть в более простую [11], так что, по существу, одна и та же величина напряжения последовательно снимается с нескольких разных сетей. Полученные с их помощью искомые температурные данные можно считать вычисленными с определенной точностью либо использовать их как начальное приближение для последующего уточнения при требованиях повышенной точности.

Принципиальная схема и расчетная модель измерительной сети

Рассмотрим принципиальную схему на рис. 1. «Опорное» постоянное напряжение E 1 подается на последовательную цепь «делителя напряжения» из резисторов R ₀, R i,..., R n . Пилообразное напряжение E ₂ подается на общий контакт n пар диод-терморезисторов D 1 + T 1 ,., D_n + T n , которые подключены между соседними резисторами «делителя напряжения».

Значения сопротивлений терморезисторов являются искомыми величинами. Для их определения используются два заданных значения E 1 , E ₂ и измеряемый ток I по показаниям амперметра A . Затем сопротивление каждого терморезистора пересчитывается в его температуру с учетом графика строгой монотонной зависимости сопротивления от температуры. При наличии вольтметра измерение тока можно заменить измерением падения напряжения на резисторе R ₀ с исключением из цепи амперметра A .

Геометрически реализация схемы осуществляется путем компактного последовательного расположения троек D k + T k + R k , соединяемых с соседями двумя проводниками по всей длине – 285 –

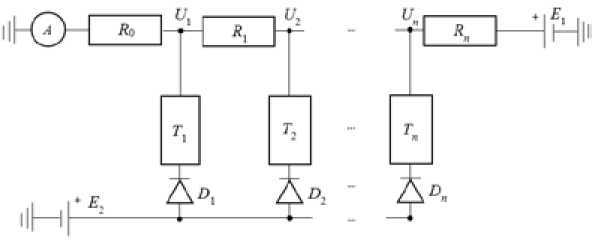
Рис. 1. Измерительная схема

Fig. 1. Measuring circuit

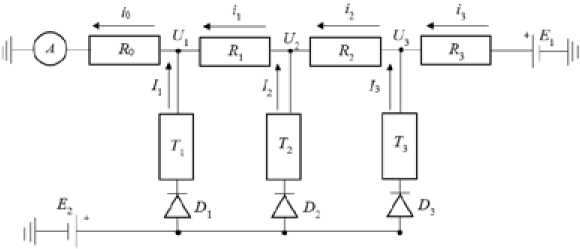
Рис. 2. Направления токов в схеме с тремя терморезисторами

Fig. 2. Directions of currents in the circuit with three thermistors цепи, располагаемой по площади или объему контролируемого изделия. Третий провод используется только в конце измерительной сети для подачи опорного напряжения. Использование общего заземления (например, на металлоконструкциях) может вообще устранить его протяженную реализацию.

Для упрощения обозначим численные значения сопротивлений резисторов R k , диодов D k и терморезисторов T k одноименными символами с этими элементами схемы. Для формирования математической модели зафиксируем эти сопротивления и напряжения E 1 , E ₂. Ток, входящий в к -тый узел со стороны к +1-го узла, обозначим через i k , а ток со стороны к -той измерительной пары D k + T k - через I k . Величина i ₀ соответствует току, выходящему из первого узла в сторону заземления. Выбор знаков поясняется на рис. 2 для трех измерительных пар. Выпишем первый закон Кирхгофа для токов в узлах с номерами k = 1,…, n [11]:

^- i о + i j + I j - 0,

• — i j + i 2 + 1 2 — 0,

• - i n — 1 ⁺ i n ⁺ I n ^— 0.

Заменим токи напряжениями по закону Ома и приведем подобные члены:

<

U 1

F⁺ к R 0

1 — T + D i

1 )

+ — -

R J

i

U. — = E, ² R 1 ²

,

T + D i

U2 \  +

² к R i T 2 + D 2

i)

+ — -n R 2 J

u1 — - U3 — = E2

R ₁      R ₂

T2 + D2’

U n

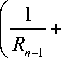
T n + D n

+

R n

-

n-i p         2

R n - 1

T + D nn

+ E .

1 _Rn

В результате получилась система линейных алгебраических уравнений метода узловых потенциалов с трехдиагональной матрицей для определения неизвестных U1, U2,., Un. Матрица неразложима, имеет диагональное преобладание, причем строгое в первой и последней стро ках [12]. Поэтому она невырождена и при положительных E1, E2 все потенциалы Ub U2,..., Un тоже положительны [12]. Вообще говоря, все уравнения системы (2) можно записать в одно- родной форме

- U k - 1 — + U k

Rlr _1

( 1

I R - 1 ⁺

T k + D k

1 )

⁺ T I- U k + 1 R k )

— = E.

R k ²

T k + D k

для k = 1,..., n (3)

с учетом «краевых значений» U 5 = 0 и U n +1 = E 1 .

Проиллюстрируем основную идею в частном случае с тремя терморезисторами, представленном на рис. 2. В этом случае система (2) записывается в виде

[	Л 1	1	1 ^	1	1
U	—	+	+ —	- Eo--	U 2 — = 0,
1	v R 0	T i + D i	R i J	2 T 1	2 R 1
	(	1	1	1	1               1
U		+	+	- и —	- E2--U — = 0,
2	V R 1	T 2 + D 2	R 2	1 R i	2 T 2 3 R 2
	(	1	1	1	1          1
U		+	+	- и—	- E , — - E — = 0.
1 3	V R 2	T 3 + D 3	R 3	2 R 2	2 T 3 1 R 3

Процесс нахождения неизвестных сопротивлений терморезисторов T 1 , Т₂ и Т ₃ состоит из последовательного рассмотрения трех состояний измерительной схемы: U , < E ₂< U ₂, U ₂< E ₂< U , и E 2 > U > .

При U|

U1

' 1      1      1 )

11 Ro  T  R J

- E, — - U — = 0, 2_T12_R1

Г2

^U3

-+- 1

IR R2 J

- u. — - и — = 0, 1_R13_R2

Г 1       1

—+— I

I R2 ^R3 J

- U2 — - E1 — = 0.

R₂     R₃

Из первого уравнения следует, что

T =( U1 - E2)

U известно, поскольку является (измеренным) падением напряжения на фиксированном резип тт                    п А п + т сторе R0. U2 при «разомкнутых» ветвях D2 + Т2 и D3 + Т3 определяется делителем напряжения между потенциалами E1 и Ui

U2 = (Ei -U,)RJ(Ri + R₂+ R3).

В итоге, все величины в (6) известны и однозначно определяют T1.

При открытых диодах D 1 и D₂ (U₂<E₂<U_;) система (4) принимает вид

	1	1	1 1	_ 1	1
U	— +	--+	— -	- E,--	- U2 — - 0,
11	R0	T1	R1J	2T1	2R1,
	Л1	1	11	1	1           1
U	— +	+	—	- U1 —	- E2--U —
21	< R1	T2	R 2 J	1R1	2T23R2
	' 1	1 ^		1	1 „
U	+		- иг 2	--Ex 1	— - 0.
31	. R 2	R3 J			R

- 0,

Из второго уравнения следует, что

T=₍- E)/[ и₊u - U

Ii 1

+

I R R2

U₂ = RU1

-1 + -1

R0T1

+--

R1

—

R1

^E2    .

T1

U₃ при «разомкнутой» ветви D₃ + T₃ определяется делителем напряжения между потенциалами

E1 и U₂:

Uз = (Ei — U₂) R₂/( R₂+ Rз).

В итоге, все величины в ⁽⁸⁾ известны и однозначно определяют T

При E2>U3 все диоды открыты. Тогда из третьего уравнения системы (4) вытекает, что

/I U E, l R 2 +Rз" 3

U₃

= ^R 2U 2

— + —+-

—

R1T2R2

R R

U RL—ER². 1_R12_T2

^Подс^{тавляя их в (10)}, однозначно определяем величину T3.

В случае большего количества троек D_k + T_k + R_k вычисление T_k осуществляется аналогично по нарастанию индекса k от 1 до n в момент подачи напряжения E2 ∈(Uk, Uk–1) для открывания диодов D₁,…, D_k = 0 при закрытых диодах D_k+1,…, D_n = +∞. К этому моменту считаются вычисленными величины T1,…, Tk–1. Тогда из уравнения (3) получаем

J[ U_k-1 U_k+1    [ 11

.

Tk^-(Uk ^-E 2 )          '         Uk|       '

/ (Rk-1    Rk        I Rk-1   Rk.

Участвующие в этой формуле Uk–1 и Uk вычисляются из уравнений (3) с нулевыми Di:

Ui- Ri-1

- ^U+u .

Ri-2       '^-1

+”+

-

Ri-2   T-1

Ri-1

E2)

T-1^J

для i — 2,...,k.

А Uk–1 вычисляется из других уравнений (3) с бесконечными Di, что численно реализуется в виде делителя напряжения между E1 и Uk:

Uk+1 - (E1 - Uk) Rk/(Rk +...+Rn+1).

Вычислительный эксперимент

Рассмотрим модельную задачус «идеальными» диодами. Пусть E1=5В, R0=R1=R2=R3=900Ом, T₁=2000 Ом, T₂=3000 Ом, T₃=4000 Ом. Для расчета параметров электрической цепи применяли описанный метод узловых потенциалов. В тестовых расчетах использовались «идеальные» диоды в следующем смысле: у открытого диода сопротивление равно нулю, а у закрытого – проводимость равна нулю. Отметим, что эти условия плохо выполняются при незначительном падении напряжения на реальном диоде. Поэтому при измерениях следует избегать ситуаций, близких к точкам переключения диодов.

Сначала проведем вычисление узловых потенциалов при изменении постоянного напряжения E2 в интервале [0.2, 5.0] c шагом 0.2. Полученные значения представлены в табл. 1-4.

В качестве исходных данных для работы алгоритма были выбраны три ситуации с разными состояниями диодов:

• 1)    состояние 8: E₁=5.0 В, E₂=1.8 В, U₁=1.39 В;

  Таблица 1. Все диоды находятся в закрытом состоянии

  
  

  Table 1. All diodes are in the closed state

  Такт акт	E2, В	U1, В	U2, В	U3, В
  0	0.20	1.25	2.50	3.75
  1	0.40	1.25	2.50	3.75
  2	0.60	1.25	2.50	3.75
  3	0.80	1.25	2.50	3.75
  4	1.00	1.25	2.50	3.75
  5	1.20	1.25	2.50	3.75

  
  

  Таблица 2. Диод D1 открыт, D2 и D3 закрыты

  Table 2. Diode D₁ is open, D₂ и D₃ are closed

  Такт	E2, В	U1, В	U2, В	U3, В
  6	1.40	1.29	2.53	3.76
  7	1.60	1.34	2.56	3.78
  8	1.80	1.39	2.59	3.80
  9	2.00	1.44	2.63	3.81
  10	2.20	1.49	2.66	3.83
  11	2.40	1.54	2.69	3.85
  12	2.60	1.59	2.73	3.86

  
  

Таблица 5. Результаты вычислительного эксперимента

Table 5. Results of the computational experiment

Открытые диоды	U2, В	U3, В	Ti, Ом
D1	2.59	3.79	T1 = 2000.20
D1, D2	2.91	3.95	T2 = 3000.29
D1, D2, D3	3.42	4.25	T3 = 4000.55

Таблица 3. Диоды D₁ и D₂ открыты, D₃ закрыт

Table 3. Diodes D₁ and D₂ are open, D₃ is closed

Такт	E2, В	U1, В	U2, В	U3, В
13	2.80	1.65	2.77	3.88
14	3.00	1.71	2.83	3.92
15	3.20	1.77	2.91	3.95
16	3.40	1.84	2.98	3.99
17	3.60	1.90	3.05	4.02
18	3.80	1.97	3.12	4.06
19	4.00	2.04	3.19	4.09

Таблица 4. Диоды D₁, D₂ и D₃ открыты

Table 4. Diodes D₁, D₂, and D₃ are open

Такт	E2, В	U1, В	U2, В	U3, В
20	4.20	2.10	3.26	4.14
21	4.40	2.17	3.34	4.19
22	4.60	2.24	3.42	4.25
23	4.80	2.31	3.50	4.31
24	5.00	2.38	3.59	4.36

• 2)    состояние 15: E1=5.0 В, E2=3.2 В, U1=1.77 В;

• 3)    состояние 22: E1=5.0 В, E2=4.6 В, U1=2.24 В.

Полученные результаты работы алгоритма представлены в табл. 5.

Ошибка восстановления сопротивлений T₁, T₂, T₃ составила менее 0.014 %.

Заключение

Ясно, что в реальных схемах вольтамперные характеристики диодов не столь идеальны. Поэтому ошибка восстановления сопротивления термисторов получается тем больше, чем больше отклонения характеристик диодов от идеального состояния, т.е. чем больше выражения

_Dkop / Tk и Tk /D_k^cl                                                               (15)

для открытого D_k^opи закрытого D_k^clсостояний диодов соответственно. Точность будет тем выше, чем меньше величины (15), которые необходимо учитывать при подборе реальных элементов измерительной схемы.

Снижение точности может происходить при большом числе троек Dk + Tk + Rk, когда ненулевые обратные токи суммарно могут дать существенный вклад в погрешность изложенного алгоритма. Тогда изложенный алгоритм применяется для получения начального приближения для решения полной системы нелинейных алгебраических уравнений (3), в которых сопротивления Dk, в принципе, не только зависят от направления тока, но и могут нелинейно зависеть от амплитуды напряжения и даже от температуры. В таком случае для решения нелинейных – 290 – систем уравнений, получающихся при каждом конкретном режиме включения диодов, должна быть известна (нелинейная) температурная вольтамперная характеристика используемых диодов.

Исследование выполнено при финансовой поддержке Российского фонда фундаментальных исследований, Правительства Красноярского края, Красноярского краевого фонда науки в рамках научного проекта: № 18-47-242005 «Создание эффективных распределенных сетей температурных датчиков для бортовой аппаратуры спутников».