Термостатирование непрерывнолитого слитка в МНЛЗ для обеспечения прямой прокатки

В связи с тем, что в черной металлургии большое значение придается снижению потребления энергии, процесс прямой прокатки, предусматривающий подачу горячих непрерывнолитых заготовок непосредственно на прокатный стан, имеет перспективное направление развития [1–9].

Основной предпосылкой для применения этого процесса является сохранение теплосодержания непрерывнолитого слитка для последующей прокатки. При сохранении теплоты жидкой сердцевины слитка возможно уменьшить (или исключить) промежуточный нагрев в нагревательных печах и непосредственно передавать слитки на прокатный стан.

Высокотемпературные режимы литья слябов на установке непрерывной разливки стали (УНРС), позволяющие применить прямую прокатку, описаны авторами [10–13].

Реализация схемы «непрерывная разливка – прямая прокатка» предлагается с полным или частичным подогревом углов и граней слитка [14, 15]; с помощью автоматизированного управления линией «машина непрерывного литья заготовок (МНЛЗ) – прокатный стан» [16, 17]; применением защитных шлаковых смесей с высокой температурой плавления; ускоренной транспортировкой слитков [10, 13, 16] и т. п.

В настоящее время режимы охлаждения и затвердевания непрерывнолитого слитка не обеспечивают равномерного распределения температур по его сечению, перепад между поверхностью и центром на выходе из МНЛЗ при различных скоростях вытягивания составляет от 250 до 500 °С [18–22].

Для сохранения теплоты расплава и обеспечения равномерного распределения температур по сечению слитка в конце МНЛЗ предлагается использовать теплоизолирование [23] вместо его охлаждения в зоне воздушного охлаждения.

Для математического моделирования температурного поля непрерывнолитого слитка решалось уравнение теплопроводности в двумерном пространственном представлении с учетом выделения внутренних источников теплоты q_v в интервале температур солидус– ликвидус [23, 24]:

<д T A

Р э ( ^T ) C э ( ^T )| — I = div (^Х э ( Т ) grad^T ) + q v .

V дт у

Принималось, что выделение теплоты плавления происходит по линейному закону в соответствии с правилом рычага [19]. Скрытая теплота кристаллизации определялась как величина относительного количества твердой фазы ф :

С _т – теплоемкость твердого металла; Т _л

температура ликвидуса; Т _с солидуса.

–

–

температура

Величина эффективной теплопроводности рассматривалась как [19]:

ГХ ж ,при T >  T л ;

(T И

^Х т ^+Х ж

Т _Т

V ^с 1 л

при T с <  T <  T;

X _т, при T_с <  T , где X ж - теплопроводность жидкого металла; Х _т - теплопроводность твердого металла.

Запишем величину эффективной плотности металла [25]:

Рэ ( TM

^Р т ^{+ Р} ж +  ¹

Т -Т т

V л с    хл

при Т с <  T <  T л ; Р _т,при T <  T_с,

q кр   A

-

т

Т с у

( T - T с ) ,

x

Ф =----- ,

У расп

где x – объем выделившейся из расплава твердой фазы; V _расп – объем всего расплава.

Величина плотности внутреннего источника теплоты в этом случае рассчитывалась как

(дфА qv = qкрр1 3 I ,

V дт J

где qкр – скрытая теплота кристаллизации, кДж/кг; — - скорость затвердевания сплава.

В соответствии с [19, 20] эффективная те плоемкость Сэ зависит от температуры слитка

и задается в виде системы:

' C ж^,п ри ^T >  ^т _л;

Сэ ( T Н

C _т +

(г т + '-'ж

Т — Т

V л с

q _кр

т

л

-

\

т

Т с У

( T - T c ) ,

при T c <  T <  Т _л; C _т,при T <  Т с ,

где С _ж – теплоемкость жидкого металла;

где р _ж - плотность жидкого металла; р _т -плотность твердого металла.

Начальные условия состоят в задании для начального момента времени т = т ₀ распределения температур T ( x , у , т ₀ ) .

Граничные условия отображают условия теплового взаимодействия между окружающей средой и поверхностью слитка для каждой определенной в модели зоны [25]. В зоне теплоизолирования для анализа распределения теплоты составлен тепловой баланс.

Решение уравнения теплопроводности теплоизолирующего устройства осуществлялось численными методами расщепления по координатам (дробных шагов) [26], аналогичными тем, которые использовались при решении уравнения теплопроводности для слитка [25]. Реализация алгоритма осуществлялась на языке программирования C++. Адекватность модели проверялась по сходимости расчетных и экспериментальных значений температуры поверхности слитка с помощью критериев Фишера, Стьюдента и непараметрического критерия Манна – Уитни [24, 25].

В результате проведенного численного эксперимента было получено температурное поле непрерывнолитого слитка прямоугольного сечения 250 x 1100^2350 мм по длине МНЛЗ при скоростях разливки 0,6–1,4 м/мин.

На рис. 1 пок аз ан график и зоте рм с оли д у с а для ра зли чн ых с к о рос тей ра зли в к и п о д ли н е МНЛЗ c и спол ьзов а н и е м те п л оизол иров а н и я в зоне воздушного охлаждения.

Рис. 1. Изотермы солидуса по длине МНЛЗ в зависимости от скоростей вытягивания слитка

В секциях зоны водо- во зду ш ного охла жд ен и я и н т е н с ив н о с ть теп лоо тд а чи ре г у ли ро в а ла с ь из м енением р асх о да во ды с по м о щью перекл юч ающей ф ункции. К р итер ием вы бо р а коэффициента а из ди апаз он а 1 0 0-650 Вт/(м²К) было п о лн ое за тв е р д е в а ни е с ли тка п е ред е г о по р ез о м на м ер ны е дл ины и о беспеч ение сре днем ассо во й т ем пер атур ы не ниж е 1 2 0 0 °С.

Длина зоны теплоизолирования принималась 17 м [27].

По результатам моделирования можно сделать вывод о том, что при использовании зоны теплоизолирования затвердевание слитка происходит при скоростях до 1,3 м/мин. При более высоких скоростях вытягивания для полного затвердевания слитка перед порезкой необходимо увеличить интенсивность охлаждения в зоне вторичного охлаждения (ЗВО).

После зоны водо-воздушного охлаждения происходит либо охлаждение слитка на воздухе, либо его теплоизолирование. Для сравнения перепадов температур между поверхностью широкой грани и центром слитка при его охлаждении на воздухе 8во с выравнива- нием температур при теплоизолировании 8т введем симплекс отношения степеней выравнивания температур в5:

P_s=^.

⁵   8 во

Учитывая, что начальная разность температур A 1 ₀ после ЗВО одинакова, то

Р5_^т-

⁵   5 во

^A t (т)

^A t 0(т) _ ^A t ( т )

^A t (во)     ^A t ( во )

^A t 0(во)

.

На рис. 2 приведен коэффициент в ₅ , который характеризует эффективность выравнивания температур по сечению слитка при применении зоны теплоизолирования.

Длины зон водо-воздушного охлаждения и теплоизолирования (охлаждения на воздухе) выбирались постоянными для всех скоростей. По результатам моделирования можно сде-

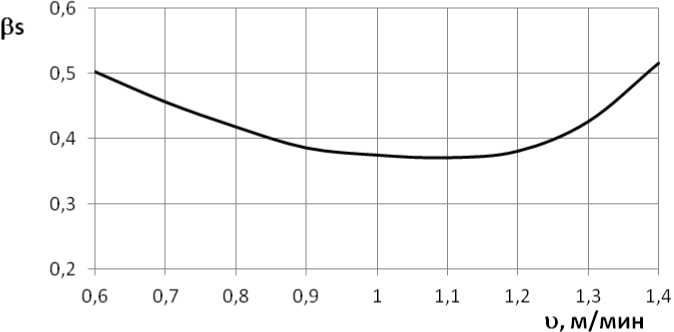
Рис. 2. Зависимость β _s от скорости вытягивания слитка

Отношение степеней выравнивания температур угла

Скорость вытягивания, м/мин	Δ t (во) при в озд. охлажд., °С	Δ t (т) при теплоизолир., °С	Отношение степеней выравнивания температур, β у
0,6	295	194	0,657
0,7	331	198	0,598
0,8	366	200	0,546
0,9	408	216	0,529
1,0	432	218	0,505
1,1	475	238	0,501
1,2	514	267	0,519
1,3	551	293	0,532
1,4	593	335	0,565

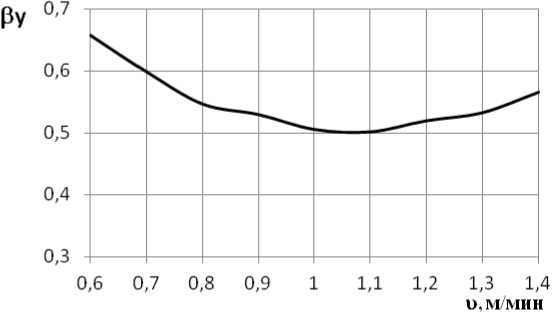
Рис. 3. Зависимость βу от скоростей разливки

лать вывод о том, ч т о п р и п ри ме н е н и и те п ло и золи ров а н и я п рои с ход ит уме н ьше н и е ра зн о сти т ем п ера тур ме ж ду п ов е рхн ос тью ш и рок ой г р ани и цент р о м сл ит ка по ср авнению с о х лаждением его на воздухе на 100 – 220 °С. Сред н ем ас с ов а я т е мп е ра ту ра в за в и с и мос ти от скорости разливки повышае т ся н а 160–260 °С.

Увеличение β _s при с к оростя х в ытяги вания слитка 1,2–1,4 м / м ин связа н о с тем , что в рем ени д ля в ы ра в н и вани я тем п е ратур по се ч е н ию сли тк а в зон е т еп л оизол иров а н и я не дос та точн о и те мп е ра ту рн ый п е ре п а д п о е г о сечению увеличивается.

По аналогии введем β _у – отн ош е ни е с те п е н и в ы ра вн ив а ни я темп ера т у р ме жду ц е нтром и у г лом сли тк а п ри е го ох ла жд е н и и н а воз ду хе к вы р авниван ию пр и т еп л о и з о л ир о ван ии.

Р ез у льтаты с ра в н е н и я п е ре п а дов те мпе р а тур и отн ош е н и я с теп е н е й в ыра в н и в а н и я температур угла β _у пред с тав ле н ы в та б ли це и на рис. 3.

Выводы

В результате моделирования охлаждения непрерывнолитого слитка с использованием теплоизолирования получены следующие результаты: среднемассовая температура слитка увеличивается на 160–200 °С, температура центра на 100–170 °С; температура поверхности широкой грани на 270–310 °С, температура узкой грани на 225–270 °С, температура угла на 250–350 °С. Таким образом, теплосодержание слитка за счет использования теплоты жидкой фазы увеличивается на ~ 30 %, что позволяет применить прямую прокатку. Полученные расчетные значения степени выравнивания температуры по сечению слитка при воздушном охлаждении к выравниванию температур при теплоизолировании для широкой грани составляют β _s ~ 0,6–0,7, по углу – β _у ~ 0,5–0,6 при скоростях вытягивания 0,6–1,2 м/мин.