Термоупругость плоской регулярной фермы ортогональной структуры
Автор: Рыбаков Л.С.
Статья в выпуске: 2, 2017 года.
Бесплатный доступ
Изучается линейная термоупругость плоской регулярной фермы, составленной из четырех семейств прямых однородных стержней. Стержни двух из них взаимно ортогональны и формируют прямоугольные ячейки, повторяющиеся в двух перпендикулярных направлениях. В другие два семейства объединены по-разному ориентированные диагональные стержни ячеек. Все стержни работают только на растяжение-сжатие, а их упругие линии принадлежат одной плоскости. Смежные стержни жестко связаны между собой в узлах фермы - точках пересечения упругих линий взаимно ортогональных стержней. Регулярность фермы предполагает неизменность термоупругих и геометрических параметров стержней в пределах одного семейства. Внешние воздействия на ферму принадлежат ее плоскости и в общем случае включают узловые силы, погонные осевые силы стержней и их неравномерный нагрев. Строгая линейная термоупругость фермы построена с помощью метода склейки. Согласно этому методу ферма расчленялась на стержни и узлы - элементы фермы. К изолированным элементам прикладывались заданные внешние воздействия и силы взаимодействия их с соседями. Затем проводился аналитический термоупругий анализ стержней с учетом геометрических условий сопряжения смежных элементов и анализ равновесия узлов. Построенная термоупругость сформулирована в терминах узловых перемещений, полных удлинений и начальных внутренних усилий стержней. Все эти переменные - функции двух целочисленных аргументов, использованных для нумерации элементов фермы. Полная замкнутая система уравнений термоупругости фермы представлена геометрическими и физическими соотношениями, уравнениями равновесия узлов и уравнениями совместности полных удлинений стержней. С их помощью даны альтернативные постановки дискретных краевых задач. Применение теории проиллюстрировано точным аналитическим решением задачи о термоупругом деформировании фермы без внутренних узлов.
Линейная термоупругость, метод склейки, плоская регулярная ферма ортогональной структуры
Короткий адрес: https://sciup.org/146211671
IDR: 146211671 | УДК: 539.3 | DOI: 10.15593/perm.mech/2017.2.08
Текст научной статьи Термоупругость плоской регулярной фермы ортогональной структуры
PNRPU MECHANICS BULLETIN
Фермы – весьма распространенная разновидность стержневых систем, линейному упругому анализу которых посвящена обширная литература. Методы такого анализа подразделяются на континуальные и дискретно-континуальные [1].
Континуальные методы [2–10] ориентированы на регулярные системы с большим количеством периодически повторяющихся элементов и предполагают замену реальной системы конструктивно-анизотропным телом. Конкретные их реализации отличаются друг от друга видом выбранного континуального эквивалента системы и процедурой кон-тинуализации. Примером их могут служить известные теории сетчатых пластин и оболочек [4, 6]. Следует подчеркнуть, что континуальные методы не позволяют учесть индивидуальные свойства деформирования и взаимодействия элементов системы.
Этого недостатка лишены дискретно-континуальные методы, опирающиеся на дискретно-континуальную природу стержневых систем [11–39]. Среди них в первую очередь следует назвать ставшие классическими метод сил, метод перемещений и различные их модификации. Все они носят алгоритмический характер, а их развитие с появлением вычислительной техники шло по пути применения матричного аппарата и разработки эффективных методов решения больших систем линейных алгебраических уравнений [35–39].
Значительную популярность среди дискретно-континуальных методов завоевал метод конечных элементов [40–43]. Обладая возможностями не меньшими, чем классиче- ские методы, он получил широкое распространение благодаря известным программным комплексам, реализующим его универсальный алгоритм.
Среди других методов дискретно-континуального анализа регулярных стержневых систем выделим метод склейки [44–48]. Суть его в членении системы на элементы и проведении поэлементного анализа с учетом геометрических условий сопряжения смежных элементов. Эта процедура позволяет строить строгие дискретные теории упругости, вид которых предопределяется структурой изучаемой системы. Определяющие соотношения таких теорий представляются геометрическими и физическими зависимостями, уравнениями равновесия и уравнениями совместности деформаций в терминах обобщенных смещений, полных деформаций и начальных внутренних сил стержней – функций дискретных аргументов, используемых для нумерации элементов системы. Эти соотношения образуют полную замкнутую систему уравнений соответствующей теории и допускают альтернативные постановки дискретных краевых задач. Во всем этом усматривается дискретная аналогия с соответствующими континуальными моделями упругих тел.
Линейная теория плоских регулярных упругих ферм ортогональной структуры изучалась в работах [44, 45]. Ниже построенная там теория обобщается на случай термоупругого деформирования ферм.
1. Линейный термоупругий анализ фермы
Рассмотрим плоскую ферму (рис. 1), представляющую собой периодическое повторение вдоль декартовых осей x σ (здесь и далее греческие индексы принимают значения 1,2) элементарной ячейки из стержней в форме прямоугольника с двумя не связанными между собой диагональными стержнями. Как видим, ферма состоит из семейств горизонтальных, вертикальных и нисходящих и восходящих диагональных стержней. Назовём их соответственно 11-, 22-, 21- и 12-стержнями (совокупно αβ-стержни). Смежные стержни жестко связаны между собой в узлах решётки – местах пересечения упругих линий αα-стержней. По предположению все αβ-стержни упругие и однородные, а стержни одного семейства одинаковые и расположены с постоянным шагом.
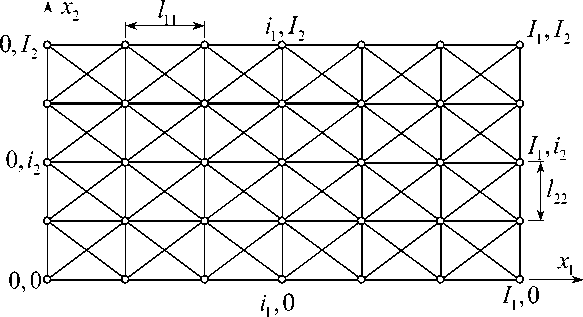
Рис. 1. Плоская ферма ортогональной структуры
Fig.1. Plane truss of orthogonal structure
В силу дискретной двухмерности фермы для нумерации ее элементов (узлов и стержней) требуются два целочисленных параметра, выступающих для переменных ве- личин в роли дискретных аргументов. Обозначим их символами i1, i2, или кратко iG, и будем считать, что они растут в направлении осей xG соответственно.
Условимся текущему узлу и исходящим из него текущим ав-стержням присваивать один и тот же номер ( i G) . Области изменения параметров i a для элементов фермы зависят от ее внешней формы. В случае ферм с прямоугольной границей (см. рис. 1) для узлов i G е [О, I а ] , где I а > 0 - заданные целые числа, для аа-стержней i G е [О, I G - 5аG ], для 12-стержней i G е [0, I G - 1], а для 21-стержней i G e [6G2, 1 G - 5g1] (6аG - символ Кронекера, а, например, [О, I а ] - замкнутый целочисленный отрезок, начинающийся с 0 и заканчивающийся I а). При иных конфигурациях фермы граничные значения параметров iG будут другими. Более того, граничные значения одного параметра могут оказаться функциями другого параметра.
Геометрические и термоупругие свойства фермы описываются длинами l а а аа-стержней (здесь и далее суммирование по повторяющимся индексам не предполагается), жесткостями g а р на растяжение-сжатие и коэффициентами аа₽ линейного расширения ав-стержней. Регулярность фермы предполагает неизменность всех этих параметров в пределах фиксированного семейства стержней. Что касается внешних воздействий на ферму, то они в общем случае слагаются из узловых сил и погонных осевых сил стержней (на рис. 1 они не показаны), включая нагрев последних.
Пусть x е [0, l а р ] - локальная осевая координата ав-стержня, а и ар ( x ), п а в ( x ) и p ар ( x )-осевое смещение, внутреннее осевое усилие и погонная осевая сила в произвольной точке упругой оси ав-стержня; U а и Ра - смещение узла и действующая на него внешняя сила в направлении оси x а, а t а в ( x ) - температура, на которую нагрет ав-стержень.
Зависимые переменные, относящиеся к стержням, являются функциями континуального аргумента x и дискретных аргументов iG , а узловые переменные - функциями только дискретных аргументов iG . Поэтому следовало бы, например, писать и а в ( x ; i 1 ,i 2), U а[ i 1 ,i 2] или кратко и а в ( x ; i G), U а [ i G ]. Ради еще большей краткости записи условимся текущие значения дискретных аргументов при символах зависимых переменных опускать вообще. С этой целью введем линейные операторы сдвига V ± , V ±± , V ^ " , смысл которых на примере отвлеченной функции V i 1 , i 2 ] = ^[ iG ] дискретных аргументов iG поясняют равенства
V ± V = V i G ± А. ], V ± 2 ± V = V i G ± 1], V ± 2 v = V[ i g + ( — 1) G ], V + V - =V - V + = 1, V ±± =V ±± =V ± V ± , V ± 2 =V " ± =V ± V " .
С помощью этих операторов образуются разностные операторы первого порядка
A ± V[ i G ] = ± v[ i G ± -v ] + V i G ], А а ± = ±V ± " 1,
A ± 2 v[ i G ] = ± v[ i G ± 1] + v[ i G ], A ± 2 =±V ± 2 ± + 1, (2)
A ±1V[ ig ] = ±V[ ig + (—1)G ] + V[ ig ], A ±1 =+V±2T+1, посредством которых формируются разностные операторы более высокого порядка. Например, для разностных операторов второго порядка, определяемых равенствами
A a ^[ i c ] = V [ i c + Sac ] - Ж i c ] + V [ i c - Sac ] ,
Д 22 Vt i c ] = Vt i c + 1] - 2v[ i c ] + Vt i c — 1], (3)
Д 21 Vtic ] = Vtic - (-1)c ] - 2v[ic ] + Vtic + (—1)c ], справедливы выражения (см. (1)-(3)):
д а =Д + Д - =Д + -Д - =V + - 2 + V - ,
A2 = A+A- = A+ - A- = V++-2 + V--
12 ла12да12 ^12 ^12 V 12 +V 12 , (V
A2 = A+A- - A' -A- -U -2-V
21 ^21^21 ^21 ^21 21 ^+ 21 .
Введенные операторы и позволяют записывать формулы и уравнения в переменных с несмещенными текущими значениями дискретных аргументов и опускать такие аргументы ради краткости записи при символах зависимых переменных. Заметим еще, что область определения дискретных аргументов i c зависимых переменных и формул или уравнений, связанных с элементами фермы фиксированного семейства, совпадает со значениями i c, участвующими в нумерации этих элементов, и повторно при названных математических объектах не указывается.
Термоупругий анализ фермы будем изучать с помощью метода склейки. Следуя ему, расчленим ферму на изолированные элементы - узлы и ав-стержни. Затем приложим к ним их собственные внешние воздействия и силы взаимодействия с ближайшими элементами. После этого проведем термоупругий анализ стержней и статический анализ узлов с учетом геометрических условий сопряжения соседних стержней и узлов фермы.
В рамках простейшего, основанного на гипотезе Дюгамеля-Неймана, варианта термоупругости деформирование нагретых изолированных ав-стержней описывают уравнения nав (x) + Pав (x) = 0, nав (x) = gавtuав (x) — %tав (x)], общее решение которых с точностью до начальных смещений uав (0) и начальных усилий
Nав = nав (0) стержней дается формулами uав (x) = uав (0) + gавNавx + uав (xX nав (x) = Nав + nав (xX xx u ав (x) =/ [aaв t ав (т) - g ав( x - Т) P ав (т)] dТ, n ав (x) = "J P ав (Т) dТ.
Полагая в первом равенстве (5) x = l ав и вводя полные удлинения стержней
Uав = Cptu ав (lав ) " ^ав (0)](7)
и обозначения uав=la1uав (lав), n:в=gави,( приходим к выражениям
Nав = gав Uав " N^в и обратным им зависимостям
U ae = g "в N ав + U ■ ■ (Ю)
Геометрические условия сопряжения начала и конца "в-стержня с соседними узлами фермы имеют вид и (0) - U , и (I ) - V*U , ""V а, аа\аа/ а а,
U 1 2(O) = cU 1 + cU 2, U 12 ( / 12 ) = V ++ ( cU 1 + cU 2 ), u 21 (0) = cU 1 - c 2 U 2 , u 21 ( / 21 ) = V + 2 - ( cU 1 - c 2 U 2 ), где c а = / аа / / 12 ■ Подставляя выражения (11) в формулу (7), получаем
U ц = / -X U 1 , U 12 = / . \ ' . ( cU 1 + c 2 U 2 ), U 22 = / 2 2 A + U 2, U 21 = / - А + 1 ( c 1 U 1 - c2U 2).
Эти формулы выражают полные удлинения U а в стержней через узловые смещения U а, а соотношения (9), (10) связывают начальные усилия N а в с удлинениями U а в стержней. По смыслу они напоминают соответственно геометрические и физические соотношения механики упругого тела. Поэтому назовем формулы (12) геометрическими, а зависимости (9), (10) - физическими соотношениями изучаемой теории.
Уравнения равновесия изолированного внутреннего узла в проекциях на декарто-вые оси x а
N аа —V - П аа ( / аа ) + c а { N 12 М / 12 ) — ( " 1) " [ N 21 "V -+ П 21 ( / 12 )]} + Р " = 0
после подстановки в них второго выражения (5) принимают вид
A " N аа + c а । А ,. N 12 " ( " 1) " А„ N 21 ] + Р ^* = 0, (13)
где внешние силовые воздействия представлены величинами
\-r~n "-(-wxj^n
1 а аа V а П ааМаа ) c "[ V 12 n12 (t12 ) ( 1) V 12 n 21V12)]. (14)
Уравнения равновесия граничных узлов, получающиеся при соответствующих значениях ia из уравнений (13) путем отбрасывания в них несуществующих величин, включая и те, что появляются после раскрытия разностных операторов, представляют собой статические граничные условия. Вместе с уравнениями равновесия внутренних узлов (13) они образуют статические соотношения изучаемой теории. В дальнейшем, ссылаясь на уравнения (13), мы будем подразумевать все статические соотношения.
Число статических искомых N а в , совпадающее с числом стержней в ферме, равно 4 1 1 1 2 + 1 1 + 1 2. Для отыскания их в свободной ферме имеется 2( 1 1 + 1)( 1 2 + 1) - 3 независимых уравнений равновесия (13). Следовательно, степень статической неопределимости изучаемой фермы равна ( 1 1 - 1)( 1 2 - 1) + 1 1 1 2 и говорит о том, что должно существовать такое же количество уравнений совместности деформаций. Проще всего они получаются путем исключения узловых смещений из формул (12).
Замечая, что для удлинений диагональных стержней, принадлежащих одной ячейке, справедливы выражения
U 12 = c 1 2 ∇ 2 + U 11 + c 2 2 ∇ 1 + U 22 + l 1 - 2 1 ( c 1 ∆ 2 + U 1 + c 2 ∆ 1 + U 2),
∇2+U21=c12U11+c22U22-l1-21(c1∆2+U1+c2∆1+U2), после суммирования их приходим к первому уравнению совместности деформаций
∑ c α2 (1 + ∇ 3 + - α ) U αα - U 12 - ∇ 2 + U 21 = 0 ( i σ ∈ [0, I σ - 1]). (16)
α = 1
Действуя на равенства (15) разностным оператором ∆ 1 -∆ 2 - , получим
∆ 1 - 2 ( c 12 ∆ 2 + U 11 + c 22 ∆ 1 + U 22 ) -∆ 1 -∆ 2 - U 12 = 0( i σ ∈ [1, I σ - 1]), c 12 ∆ 2 - 1 ∆ 2 - U 11 - c 22 ∆ 2 + 1 ∆ 1 - U 22 -∆ 1 -∆ 2 + U 21 = 0( i σ ∈ [1, I σ - 1]).
Область определения уравнения (16), (17) найдена из условия реализуемости входящих в эти уравнения разностных операторов среди полных удлинений существующих стержней. Нетрудно видеть, что область определения уравнений (16) совпадает с числом ячеек, а область определения уравнений (17) с числом внутренних узлов фермы. Посредством формул (15) первое из равенств (17) переводится во второе и наоборот, что говорит об их эквивалентности. Можно показать, что в рамках геометрически линейной теории они выражают один и тот же смысл – равенство нулю суммы изменений прямых углов, образуемых на пересечении αα-стержней во внутреннем узле фермы.
Любое из равенств (17) можно было бы принять за второе уравнение совместности деформаций. Отдадим, однако, предпочтение разности этих уравнений,
∑ c α2 (1 + ∇ α - ) ∆ 32-α U αα -∆ 1 -∆ 2 - ( U 12 - ∇ 2 + U 21 ) = 0 ( i σ ∈ [1, I σ - 1]), (18)
α = 1
включающей удлинения диагональных стержней одной и той же ячейки равноправно.
Уравнения (16), (18) порождают однородные системы линейных алгебраических уравнений относительно полных удлинений стержней U αβ . Порядок системы, порождаемой уравнением (16), равен I 1 I 2 и совпадает с числом ячеек фермы, а порядок системы, порождаемой уравнением (18), равен ( I 1 - 1)( I 2 - 1) и совпадает с числом ее внутренних узлов. Совокупный порядок обеих систем равен ( I 1 - 1)( I 2 - 1) + I 1 I 2 и, как и должно быть, совпадает со степенью статической неопределимости фермы.
Завершая вывод основных уравнений изучаемой теории, заметим, что если на граничные узлы наложены геометрические связи, предписывающие узлам заданные смещения U α ∗ , то соответствующие уравнения равновесия заменяются геометрическими краевыми условиями вида
U α = U α ∗ ( i 1 = 0, I 1 и (или) i 2 = 0, I 2 ). (19)
2. Альтернативные постановки задач
Согласно вышеизложенному напряженно-деформированное состояние фермы определено с точностью до узловых смещений Uα , полных удлинений Uαβ стержней и начальных усилий Nαβ в них. Для отыскивания всех этих величин – функций дискретных аргументов, были получены геометрические соотношения (12), физические зависимости (9), (10), статические уравнения (13) и, наконец, уравнения совместности деформаций (18), (16). Все они образуют полную замкнутую систему уравнений, допускающую альтернативные постановки дискретных краевых задач.
Как известно, постановка краевой задачи включает в себя выбор основных, определяемых в первую очередь, неизвестных, вывод разрешающих уравнений – уравнений, предназначенных для отыскания основных неизвестных, и запись краевых условий через основные же неизвестные.
Примем сначала за основные неизвестные узловые смещения U α . С помощью зависимостей (9), (12) усилия N αβ выражаются через них формулами
∗+ ∗
αα g αα α α αα ,
N 12 = g 1 ∗ 2 ∆ 1 + 2 ( c 1 U 1 + c 2 U 2 ) - N 1 ∗ 2 ,
∗+ ∗ ∗ - 1
21 = g 21 21 ( c 1 1 c 2 2 ) 21 , g αβ = g αβ αβ .
Подставляя их в равенства (13), приходим к системе уравнений
LαUα+c1c2L-U3-α+Fα=0, с разностными операторами
∗ 22 ∗ 2 ∗ 2
α g αααα + , ± g 12 12 g 21 21
и обусловленными внешними воздействиями на ферму свободными членами
∗-∗ -∗ α -∗
α = α α N αα c α [ 12 N 12 () 21 N 21 ].
Система (21) уравнений в частных разностях четвертого совокупного порядка предназначена для отыскания узловых смещений. Ее следует дополнить краевыми условиями.
Геометрические граничные условия сохраняют вид (19). Чтобы записать статические граничные условия в основных неизвестных, необходимо сначала расписать уравнения равновесия свободных граничных узлов в усилиях N αβ , после чего заменить в них эти усилия выражениями (20). Однако более предпочтителен иной путь. Если при выводе уравнений (21) принять, что ферма дискретно неоднородная в отношении упругих свойств ( g αβ = g αβ[ i σ]), то вместо равенств (22) получим
L -∗ + 2 - ∗ + - ∗ + α =∆ α g αα ∆ α + c αL + ,L ±=∆ 12 g 12 ∆ 12 ± ∆ 21 g 21 ∆ 21. (24)
И теперь уравнения (21) можно считать справедливыми для всех свободных узлов, если считать, что фактическое начертание сопровождающих их формул (23), (24) для любого свободного, в том числе и граничного, узла получается путем отбрасывания в них после раскрытия разностных операторов членов, содержащих жесткости несуществующих стержней, и возврата прежних значений жесткостей существующих стержней.
Изложенная процедура дает возможность записывать уравнения равновесия узлов в перемещениях и для нерегулярных ферм, вписываемых в структуру изучаемой фермы.
(25) i c-K aa (1 + V +- . ) N„ - K„ N „ - К ,.^ N „ = U , ( i . E [0, I , - 1]), a = 1
в которые переходят уравнения совместности деформаций (18), (16) после исключения из них с помощью соотношений (10) удлинений U ae . В равенствах (25) использованы обозначения
,, a = " (26)
U + = U - 2 +V , U ;_ - £ c a2 (1 + V + , ) U a, , K a, = g - (a * P).
a = 1
Систему четырех уравнений (13), (25) можно свести к системе двух уравнений путем построения общего решения уравнений равновесия с точностью до двух функций целочисленных аргументов ia . В изучаемой теории они играют ту же роль, что и функции напряжений в механике упругих тел. Условимся называть их силовыми функциями и представим общее решение уравнений равновесия (13) в виде суммы:
N ae = N 0в + N e , (27)
где N 0в — общее решение соответствующих однородных уравнений равновесия (13):
A - N 0a + c a [ Л - 2 N 0 - ( - 1) a A - 1 N »] = 0, (28)
а N p — какое-либо частное решение неоднородных уравнений (13), т.е.
A a N a p a + c a [ Л (2 N 1 p - НГ A 21 N p ] + P = 0.
За Np можно, например, принять усилия в стержнях какой-либо основной системы метода сил или же отредактированное должным образом решение i1 i2
N p [4, i 2 ] =- i P U < 2 ]. N £[ i 1 ,i 2 ] = - i Р Д i 1 ,j ], N p = N P - 0. j = 0 j = 0
В конкретных случаях нагружения зачастую бывает проще воспользоваться эвристическими соображениями, согласно которым за нетривиальные значения N p в исходной ферме принимаются соответствующие усилия в любой ее подсистеме, способной нести заданную нагрузку.
Приступая к отысканию общего решения N ''.. однородных уравнений равновесия (28), заметим, что с помощью соотношений
Л ± 2 =A ± +V ± A ±_ a =A ±_ a +A ± V ±_ a ,
-(-1)a A±1 = V± (A: - A ) = V^ (A± - A±-a)
Вытекающих из формул (1)-(4), они преобразуются к виду д-гм0 fv- м0 + v+TV011 + сА- (N0 -V+7V01 = O
^a [ Na a+ ca ( V 3-a N12 + V2 N 21)] + ca £A3-a (N12 V2 N 21) v и будут выполнены, если положить
N α0α + c α ( ∇ 3 - - α N 102 + ∇ 2 + N 201 ) = c α ∆ 3 - - α Ω α , N 102 - ∇ 2 + N 201 =-∆ α -Ω α . (29)
Здесь Ω α =Ω α[ i σ] – вспомогательные произвольные функции дискретных аргументов i σ . Левая часть последнего равенства не зависит от индекса α . Правая часть его будет обладать таким же свойством, если положить Ω α = 2 ∇ α +∆ 3 + - α Φ , где Φ = Φ [ i σ ] – первая силовая функция. Тогда равенства (29) принимают вид
N α0α + c α ( ∇ 3 - - α N 102 + ∇ 2 + N 201 ) = 2 c α ∇ α +∆ 32 - α Φ , N 102 - ∇ 2 + N 201 =- 2 ∆ α +∆ 3 + - α Φ .
Вторую силовую функцию Ψ=Ψ [ i σ ] введем посредством соотношения
N 1 0 2 + ∇ 2 + N 2 0 1 = - 2 Ψ .
Из трех последних зависимостей находим общее решение уравнений (28) N α0α = c α [(1 + ∇ + α ) ∆ 32 -α Φ+ (1 + ∇ 3 - -α ) Ψ ], N 1 0 2 =-∆ 1 +∆ 2 +Φ-Ψ , N 2 0 1 =∆ 1 +∆ 2 -Φ- ∇ 2 -Ψ ,
а затем и искомое общее решение неоднородных уравнений равновесия (13) N αα = c α [(1 + ∇ α + ) ∆ 32 - α Φ+ (1 + ∇ 3 - - α ) Ψ ] + N α p α ,
N 12 =-∆ 1 +∆ 2 +Φ-Ψ+ N 1 p 2, N 21 =∆ 1 +∆ 2 -Φ- ∇ 2 -Ψ+ N 2 p 1.
В том, что это так, убеждает непосредственная подстановка решения (30) в систему (28), обращающая их в тривиальные тождества.
Подставляя выражения (31) в равенства (25), приходим к искомой системе двух разрешающих уравнений в частных разностях
R 1 Φ+ R - Ψ= F 1 ( i σ ∈ [1, I σ - 1]), R + Φ+ R 2 Ψ= F 2 ( i σ ∈ [0, I σ - 1]).
Здесь слева введены разностные операторы (1)–(4)
R1 = κ11( ∆ 1 2 + 4) ∆ 4 2 + κ22( ∆ 2 2 + 4) ∆ 1 4 + κ +∆ 1 2 ∆ 2 2,
R±=(1+∇1±)(1+∇2±)(κ11∆22+κ22∆12)+κ-∆1±∆2±,(33)
R2=κ11(∆22+4)+κ22(∆12+4)+κ+, а справа – величины
F 1 =∆ 1 -∆ 2 - ( U 1 p 2 ∗- ∇ 2 + U 2 p 1 ∗ ) - ∑ c α2 (1 + ∇ α - ) ∆ 32 -α U α p α ∗ ,
2 α=1
F 2 = U 1 p 2 ∗+ ∇ + 2 U 2 p 1 ∗- ∑ c α2 (1 + ∇ 3 + -α ) U α p α ∗ ,
α = 1
в которых
∆α4=∆2α∆2α, κ±=κ12±κ21,Uαpβ∗=Uαpβ+Uα∗β,Uαpβ=gα-β1Nαpβ.(35)
Система разностных уравнений (32) предназначена для отыскания силовых функций Ф и Т . Она имеет шестой совокупный порядок по каждому дискретному аргументу. Следовательно, на границе фермы следует поставить три условия.
В свободной ферме они добываются из статических граничных условий – уравнений равновесия граничных узлов. По определению выполнение неоднородных уравнений равновесия всех узлов обеспечивается слагаемыми N α p β . Поэтому источником искомых условий служат однородные уравнения равновесия граничных узлов.
Например, чтобы выполнить уравнения (28) на границе i 2 = 0, потребуем, чтобы
<[ i i , - 1] = 0, N 02 [ i i , — 1] = 0, N 01 [ i i ,0] = 0.
Раскрывая эти равенства с помощью формул (30), находим
Ф [ i i , - 1] = 0, Ф [ i i ,0] = 0, Т [ i i , - 1] = 0.
Подобный анализ остальных границ приводит к условиям
Ф = 0 при ii =- 1,0, 1 1, 1 1 + 1 и (или) i 2 =- 1,0, 1 2, 1 2 + 1, Т = 0 при ii = - 1, 1 1 и (или) i2 =- 1, 1 2.
Вспоминая область определения усилий N αβ , обнаруживаем, что в формулах (31) фигурируют значения функции Ф и Т , отвечающие соответственно i о е [ - 1, I о + 1] и i o е [ - 1, I о ]. В силу условий (36) функция Ф имеет нетривиальные значения при i o е [1, 1 о - 1], а функция Т - при io е [0, 1 о - 1]. Как и должно быть, совокупное число нетривиальных значений этих функций совпадает с порядком системы (32), трактуемой в отношении этих значений как система линейных алгебраических уравнений.
Значения функции Ф и уравнение совместности деформаций (18), как и первые уравнения (25), (32), соотносятся с внутренними узлами фермы, а значения Т и уравнение совместности деформаций (16), как и вторые уравнения (25), (32), – с ее элементарными ячейками. При отсутствии в системе внутренних узлов уравнение (18), как и первые уравнения (25), (32), исключаются из рассмотрения. Одновременно с этим в формулах (31) и во втором уравнении (32) следует положить Ф = 0 .
Не касаясь деталей, заметим, что в тех случаях, когда на ферму наложены геометрические связи, краевые условия, накладываемые на силовые функции, устанавливаются с помощью принципа Кастильяно.
3. Некоторые аналитические и числовые результаты
Применение построенной теории проиллюстрируем на примере свободной фермы без внутренних узлов ( 1 2 = 1, рис. 2). Найдем напряженное состояние в этой ферме, полагая, что внешняя самоуравновешенная нагрузка на нее и нагрев ее стержней произвольны.
Воспользуемся для этой цели постановкой задачи в усилиях. Как отмечалось выше, в данном случае силовая функция Ф = 0 , и решению подлежит только второе уравнение системы (32). Согласно нижним краевым условиям (36) силовая функция Т , нетривиальная только при i 2 = 0 ( Т [ i о] = Т [ i i,0] = Т [ z )]), и потому является решением дискретной краевой задачи
R 2 Ψ [ i 1 ,0] = F 2 [ i 1 ,0] ( i 1 ∈ [0, I 1 - 1]), Ψ [ - 1,0] =Ψ [ I 1 ,0] = 0.
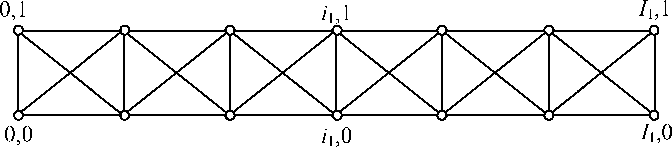
Рис. 2. Ферма без внутренних узлов
Fig. 2. Truss without internal nodes
Раскрывая здесь оператор R2 и удерживая только нетривиальные значения Ψ , после переименований i 1 , I 1 , Ψ [ i 1, 0] и ∇ 1 ± в n , N , Ψ [ n ] и ∇ ± соответственно приходим к обыкновенной разностной краевой задаче второго порядка
( ∇ +- 2η + ∇ - ) Ψ [ n ] = F [ n ]( n ∈ [0, N - 1), Ψ [ - 1] = Ψ [ N ] = 0, (37)
в которой введены обозначения
η =- 2κ 11 + 2κ 22 + κ + , F [ n ] = κ 2 - 21 F 2 [ n ,0]. (38)
2κ22
Полагая в формулах (31) Φ= 0 и сохраняя после раскрытия разностных операторов нетривиальные значения Ψ , с учетом сделанных переименований приходим к следующим выражениям для начальных усилий в стержнях:
N11[n,m]=c1Ψ[n]+N1p1[n,m] (m = 0,1), N22[n,0]=c2(1+∇-)Ψ[n]+N2p2[n,0],(39)
N 12[ n ,0] =-Ψ [ n ] + N 1 p 2[ n ,0], N 21[ n ,1] = -Ψ [ n ] + N 2 p 1[ n ,1].
Общее решение уравнения (37) имеет вид [49,50]
Ψ[n] =C1un+C2un-1+ Ψ∗[n],(40)
где Ψ∗[n] – частное решение уравнения (37), определяемое формулой n -1
Ψ∗[n] = ∑un-k-1F[k],(41)
k = 0
Здесь, как обычно, сумма считается равной нулю, если ее верхний предел меньше нижнего; C 1 и C 2 – искомые постоянные, а un (η) – полином Чебышёва второго рода степени n относительно параметра η , обладающий свойствами [51].
u - 1 = 0, u 0 = 1, un = 2η un - 1 - un - 2.
Находя из краевых условий (37) постоянные C 1 , C 2 и подставляя их в формулу (40), приходим к точному аналитическому решению:
Ψ [ n ] = Ψ ∗ [ n ] - u n Ψ ∗ [ N ] ( n ∈ [ - 1, N ]), (42)
uN предполагающему произвольными внешние воздействия на ферму и ее нагрев. Оно справедливо и для фермы, закрепленной статически определимым образом, так как она после отделения от опор и включения опорных реакций, найденных из ее глобального равновесия, в состав заданных узловых внешних сил превращается в свободную систему.
В качестве конкретного примера рассмотрим задачу о напряженном состоянии свободной фермы с десятью ячейками ( N = 10), вызванном, например, равномерным нагревом 22-стержня под номером (5,0) на постоянную температуру t 0 . В таком случае (см. (6), (8), (14), (26), (34), (38), (41), (42))
n Р = P a = P = N P = U P = 0, U P * = U ав = 5 а2 8 в2 8 „ 5 8 m 0 « 22 1 0 ,
F [ n ] = - c 21 N , (8 n 4 + 8 n 5 ), N = g 22 a 22 t 0 , T * [ n ] = - c 2 - 1 N ( hn — 5 u„ — 5 + h n — 6 u n _ 6),
^[n] = c21 N,[(uN-5 + uN-6)unuN - hn-4un—5 - hn—5un—6], где введен дискретный аналог функции Хевисайда hn =<
-
r 0 при n < 0, ^ 1 при n > 0.
Результаты вычислений по окончательным формулам (39) при laa = l и g а в = g представлены в таблице, где приведены значения не меняющихся по длине стержней фермы безразмерных усилий n aв = n aв /( g a22 t 0 ) ( n aв = N ав )'
Безразмерные усилия в стержнях фермы, вызванные локальным нагревом
Dimensionless forces in the rods of the truss caused by local heating
|
n |
n 11 ( x ; n ,0) |
n 11 ( x ; n ,1) |
n 22 ( x ; n ,0) |
n 12 ( x ; n ,0) |
n 21 ( x ; n ,1) |
|
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
0 |
0 |
|
2 |
– 0,0002 |
– 0,0002 |
– 0,0002 |
0,0003 |
0,0003 |
|
3 |
0,0032 |
0,0032 |
0,0030 |
– 0,0045 |
– 0,0045 |
|
4 |
– 0,0548 |
– 0,0548 |
– 0,0516 |
0,0775 |
0,0775 |
|
5 |
– 0,0548 |
– 0,0548 |
– 0,1096 |
0,0775 |
0,0775 |
|
6 |
0,0032 |
0,0032 |
– 0,0516 |
– 0,0045 |
– 0,0045 |
|
7 |
– 0,0002 |
– 0,0002 |
0,0030 |
0,0003 |
0,0003 |
|
8 |
0 |
0 |
– 0,0002 |
0 |
0 |
|
9 |
0 |
0 |
0 |
0 |
0 |
|
10 |
0 |
Как видно, нагрев 22-стержня с номером (5,0) порождает локальное напряженное состояние. Оно быстро затухает по мере удаления от нагретого стержня в соответствии с осциллирующим дискретным краевым эффектом, присущим изучаемой ферме для фиксированных ее упругогеометрических параметров.
Заключение
Построена линейная термоупругость плоской регулярной фермы ортогональной структуры, образованной повторением в двух перпендикулярных направлениях прямоугольной ячейки с двумя диагональными стержнями. Представленные альтернативные постановки дискретных краевых задач позволяют строить точные аналитические и численные решения различных задач статики и термоупругости обозначенных плоских ферм.
Из построенной теории могут быть извлечены частные теории регулярных и квазире-гулярных ферм ортогональной структуры, получаемых из исходной фермы удалением отдельных семейств или подсемейств диагональных стержней.
Список литературы Термоупругость плоской регулярной фермы ортогональной структуры
- Образцов И.Ф., Рыбаков Л.С., Мишустин И.В. О методах анализа деформирования стержневых упругих систем регулярной структуры.//Механика композиционных материалов и конструкций. -1996. -Т. 2, № 2. -С. 3-14.
- Sun, C. T.,Yang, T. Y. Continuum Approach Toward Dynamics of Gridworks // Transactions of the ASME // Journal of Applied Mechanics. - 1973. - Vol. 40. - No 1. - P. 186-192.
- Gutkowski W. On the analysis of plane lattice structures//J. Struc. Mech. -1973. -Vol. 2. -No. 2. -P. 159-176.
- Пшеничнов Г. И. Теория тонких упругих сетчатых оболочек и пластинок. -М.: Наука, 1982. -352 с.
- Noor A. K. Continuum modeling for repetitive lattice structures//Appl. Mech. Rev. -1988. -Vol. 41. -No 7. -P. 285-296 DOI: 10.1115/1.3151907
- Васильев В. В. Механика конструкций из композиционных материалов. -М.: Машиностроение, 1988. -272 с.
- Шклярчук Ф. Н. Упругодинамические континуальные модели длинных ферм регулярной структуры//Изв. РАН. МТТ. -1994. -№ 1. -С. 156-163.
- Tollenaere, H., Caillerie D. Continuous Modeling of Lattice Structures by Homogenization//Advances in Engineering Software. -1998. -Vol. 29. -Iss. 7-9. -P. 699-705. -URL: http://dx.doi.org/10.1016/S0965-9978(98)00034-9 (accessed: 14 March 2017).
- Boutin C., Hans S. Homogenisation of periodic discrete medium: application to dynamics of framed structures//Computers and Geotechnics. -2003. -Vol. 30. -No 4. -P. 303-320. -URL: http://dx.doi.o (accessed: 14 March 2017) DOI: rg/10.1016/S0266-352X(03)00005-3
- Messner M. C. Optimal lattice-structured materials//Journal of the Mechanics and Physics of Solids. -2016. -Vol. 96. -P. 162-183. -URL: http://dx.doi.o. 07.010 (accessed: 13 March 2017) DOI: rg/10.1016/j.jmps.2016
- Блейх Ф., Мелан Е. Уравнения в конечных разностях статики сооружений. -Харьков: Гос. науч.-техн. изд-во Украины, 1936. -383 с.
- Джанелидзе Г.Ю., Пановко Я.Г. Статика упругих тонкостенных стержней. -М.-Л.: ГИТТЛ, 1948. -208 с.
- Блейх Ф. Устойчивость металлических конструкций. -М.: Физматлит, 1959. -544 с.
- Рабинович И.М. Основы строительной механики стержневых систем. -М.: Госстройиздат, 1960. -519 с.
- Игнатьев В.А. Расчет регулярных стержневых систем. -Саратов: Изд-во Сарат. ун-та, 1973. -434 с.
- Розин Л. А. Вариационная постановка задач для упругих систем. -Л.: Изд-во ЛГУ, 1978. -223 с.
- Филин А.П. Прикладная механика твердого деформируемого тела: сопротивление материалов с элементами теории сплошных сред и строительной механики. Т. II. -М.: Наука, 1978. -616 с.
- Алгоритмы построения разрешающих уравнений механики стержневых систем/А.П. Филин, О.Д. Тананайко, И.М. Чернева, М.А. Шварц. -Л.: Стройиздат, 1983. -232 с. Ржаницын А.Р. Строительная механика. -М.: Высш. шк., 1982. -400 с.
- Шулькин Ю.П. Теория упругих стержневых конструкций. -М.: Наука, 1984. -272 с.
- Renton J.D. The Beam-Like Behavior of Space Trusses//AIAA Journal. -1984. -Vol. 22. -No. 2. -P. 273-280 DOI: 10.2514/3.8379
- Розин Л.А. Теоремы и методы статики деформируемых систем. -Л.: Изд-во ЛГУ, 1986. -276 с.
- Ржаницын А.Р. Составные стержни и пластины. -М.: Стройиздат, 1986. -316 с.
- Усюкин В.И. Строительная механика конструкций космической техники. -М.: Машиностроение, 1988. -392 с.
- Биргер И.А. Стержни, пластины и оболочки. -М.: Физматлит, 1992. -392 с.
- Леонтьев Н.Н., Соболев Д.Н., Амосов А.А. Основы строительной механики стержневых систем. -М.: ACB, 1996. -541 с.
- Розин Л. А. Задачи теории упругости и численные методы их решения. -СПб.: Изд-во СПбГТУ, 1998. -428 с.
- Елисеев В.В. Механика упругих тел. -СПб.: Изд-во СПбГТУ, 1999. -341 с.
- Hutchinson R.G., Fleck N.A. The structural performance of the periodic truss//Journal of the Mechanics and Physics of Solids. -2006. -Vol. 54. -Iss. 4. -P. 756-782. -URL: http://dx.doi.o) (accessed: 14 March 2017) DOI: rg/10.1016/j.jmps.2005.10.008
- Галишникова В.В., Игнатьев В.А. Регулярные стержневые системы. Теория и методы расчета/Волгогр. гос. архит.-строит. ун-т. -Волгоград, 2006. -552 с.
- Светлицкий В.А. Строительная механика машин. Механика стержней: в 2 т. Т. 1. Статика. -М.: Физматлит, 2009. -383 с.
- Sun H., Wang Y., Zhao W. Comparison of theories for stability of truss structures. Part 1: Computation of critical load//Communications in Nonlinear Science and Numerical Simulation. -2009. -Vol. 14. -Iss. 4. -P. 1700-1710. -URL: http://dx.doi.o. 2008.03.009 (accessed: 14 March 2017) DOI: rg/10.1016/j.cnsns
- Дарков А.В., Шапошников Н.Н. Строительная механика. -СПб.: Лань, 2010. -656 с.
- Tran H.C., Lee J. Force methods for trusses with elastic boundary conditions.//International Journal of Mechanical Sciences. -2013. -Vol. 66. -P. 202-213. -URL: http://dx.doi.org/10. 1016/j.ijmecsci.2012.11.009 (accessed: 14 March 2017).
- Современные методы расчета сложных статически неопределимых систем: сб. ст./пер. с англ. под ред. А.П. Филина. -Л.: Судпромгиз, 1961. -876 с.
- Аргирис Дж. Современные достижения в методах расчета конструкций с применением матриц. -М.: Стройиздат, 1968. -241 с.
- Martin H.C. Introduction to Matrix Methods of Structural Analysis. -New York: McGraw-Hill Book Co., 1966. -331 p.
- Meek J.L. Matrix structural analyses. -New York : McGraw-Hill Book Co., 1971. -628 p.
- Ливсли Р. Матричные методы строительной механики. -М.: Стройиздат, 1980. -224 с.
- Постнов В.А., Хархурим И.Я. Метод конечных элементов в расчетах судовых конструкций. -Л.: Судостроение, 1974. -344 с.
- Розин Л.А. Стержневые системы как системы конечных элементов. -Л.: Изд-во ЛГУ, 1975. -237 с.
- Образцов И.Ф., Савельев Л.М., Хазанов Х.С. Метод конечных элементов в задачах строительной механики летательных аппаратов. -М.: Высшая школа, 1985. -392 с.
- Zienkiewicz O.C., Taylor R.L., Zhu J.Z. The Finite Element Method: Its Basis and Fundamentals/7th Edition. -Elsevier, Butterworth-Heinemann, 2013. -756 p.
- Рыбаков Л.С. О теории одной плоской регулярной упругой структуры ферменного типа//Изв. РАН. МТТ. -1995. -№ 5. -С. 171-179.
- Рыбаков Л.С. Упругий анализ одной плоской регулярной стержневой структуры//Изв. РАН. МТТ, -1996. -№ 1. -С. 198-207.
- Рыбаков Л.С. Линейная теория плоской ортогональной решетки//Изв. РАН. МТТ. -1999. -№ 4. -С. 174-189.
- Rybakov L.S. Linear theory of an elastic prismatic framework//Mechanics of Solids. -2001. -Vol. 36. -No 4. -P. 83-93.
- Рыбаков Л.С. Линейный упругий анализ пространственной ортогональной решётки//Механика композиционных материалов и конструкций. -2016. -Т. 22, № 4. -С. 567-584.
- Jordan C. Calculus of finite differences. -New York: Chelsea Publishing Company, 1950. -652 p.
- Математические основы теории автоматического регулирования. Т.2./под ред. Б. К. Чемоданова. -М.: Высшая школа, 1977. -453 с.
- Пашковский С. Вычислительные применения многочленов и рядов Чебышева. -М.: Наука, 1983. -384 с.


