Ternary Tree Based Group Key Agreement for Cognitive Radio MANETs

Published Online September 2014 in MECS DOI: 10.5815/ijcnis.2014.10.03

The collaborative group oriented applications such as pay per TV, video conferencing, online games, etc., use a shared group key for providing secure communication. This section discusses about an efficient Group Key Agreement (GKA) protocol for Cognitive Radio Mobile Adhoc NETworks (CRMANETs).

Rapid developments in wireless technology led to the problem of shortage in unlicensed spectrum bands while licensed frequency bands are not fully utilized. The Cognitive Radio (CR) proposed in [1] can solve the problem of this spectrum scarcity by accessing the unused portions of licensed frequency bands when it is not in use. CR devices are aware of their working environment and they can dynamically change their internal parameters such as protocol used, modulation type when it detects the variations in the radio spectrums. The main challenges in CR devices are learning from the environment, intelligence and adaptability to provide the reliable and efficient communication.

In CR Network (CRN), the spectral efficiency can be improved by allowing the unlicensed users to access the spectrum allocated to the licensed users. In CRN, the CR users or Secondary Users (SUs) can employ the technique called Secondary Spectrum Access (SSA) to share the spectrums assigned to the licensed users or Primary Users (PUs). The CR devices can employ three types of transmission or spectrum access techniques such as overlay, underlay and interweave. Using the ‘Underlay’ technique of SSA, SU can coexist with PU and can use the licensed bands for their own communication [2].

In addition to the normal operations of wireless nodes, the devices in the CRN carry out some additional dynamic functions such as spectrum sensing, spectrum sharing, spectrum access, etc. The CR users perform group communication during these dynamic operations to exchange their local data in order to obtain the final result of the operations. To provide group security in CRN, the authors of [3] suggested the use of a shared group key to perform secure communication.

A Mobile Ad hoc Network (MANET) is a collection of mobile devices or nodes that can communicate with each other without any pre-determined infrastructure and links. There is no clear boundary in this network when compared to conventional wired networks. The mobile nodes are free to join and leave the network at any point of time. Hence, MANETs are more vulnerable to security attacks than wired networks due to its dynamic topology. The cryptographic techniques are used to protect this network from unauthorized users. The group key management plays an important role in securing the communication between nodes in MANETs. Several group key management techniques were used in the literature to provide secure communication. These key management schemes can be classified as a) Key distribution method and b) Contributory GKA (CGKA) method based on the method used to establish the group key.

In the key distribution methods [4-9], a single entity called the Key Distribution Center (KDC) generates and distributes individual keys and initial group key to the members in a group. It is also responsible to re-compute the new group key during the membership change. But, there is no KDC in the CGKA schemes [10-24]. CGKA requires each group member to contribute an equal share to compute the common group key. The resource restricted CRMANETs can employ CGKA scheme to generate the group key rather than distributed schemes as there is no Trusted Third Party or Certification Authority.

DH protocol [10] performs expensive modular exponentiations which require high CPU and memory capabilities. ECDH protocol [11] performs computationally efficient operations with smaller keys when compared to DH. GDH.2 [13] has less communication overhead than GDH.1 and GDH.3 [13].

It is seen in the literature that the tree based CGKA methods reduce the overall complexity to O (log n), where ‘n’ is the group size [17]. The rekeying, a process of updating the group key is classified into two categories based on the rekeying time. The Individual-based Rekeying (IR) [17-21] updates the group key after each join or leave request. The Interval based Batch Rekeying (BR) [22-24] collects join and leave requests and updates the group key after a fixed time interval so that it reduces the overall complexity [24]. Therefore, this paper proposes the use of ternary key tree and BR approach for the devices in CRMANETs.

The rest of this paper is organized as follows. Section 2 presents several representative schemes of CGKA protocols. The BR algorithms used in the proposed CGKA protocol are discussed in Section 3. In Section 4, the performance of the proposed protocol is analyzed. Finally, Section 5 concludes this paper.

• II.    Literature Review

This section reviews the tree-based CGKA schemes designed for wireless networks as they are applicable to CRMANETs too. This section discusses the CGKA protocols based on both IR and BR approach.

The TGDH [17] is the first tree based key agreement protocol that uses a special member called ‘Sponsor’ to update the group key during membership change. Every member maintains the keys of the nodes in its ‘keypath’ and ‘copath’ to calculate the updated group key after receiving a broadcast message from the sponsor. The partition event of TGDH is the most expensive operation and the group key is updated for each join and leave request.

The PACK [18] uses a tree structure called ‘PFMH’ that combines Partially Full (PF) key tree and Maximum Height (MH) key tree. The protocol refers PF subtree and MH subtree as main tree and join tree respectively. It needs O (1) round for single join operation. But the cost for single leave event is higher than the cost associated with leave event in TGDH [18]. A ternary tree based method proposed in [19] uses a ternary key tree to reduce the overall rekeying cost. Every three members are grouped to form a subgroup and the GDH.2 protocol is used to compute a group key. It restricts the group size, total number of join and leave members.

The TFAN [20] uses point multiplication operation in ECDH protocol to compute the group key. It requires less computation and communication cost for calculating the updated group key and it is efficient for partition and merge operations. The CGKA in [21] maintains a balanced binary tree using rotation operations to perform communication over multicast group, and it can support only single join and leave events. It outperforms the protocols such as DH, GDH and TGDH in terms of computational complexity since it uses point multiplication rather than modular exponentiation [21].

GKA protocols with BR approach reduce the cost associated with both the computation and communication during the rekeying process. A temporary join tree is created for new users in [22], JDH [23] and [24], and the new users are moved into the main tree when the join tree is full in [23, 24]. In [22], the temporary tree is inserted at the position of the shallowest leaving node. In JDH, the join algorithm inserts the new user at the root node of the main tree when the join tree is empty.

The protocol in [24] uses a key tree with three parts such as a) a dynamic size ‘Queue tree’ for both join and leave requests, b) a lower capacity ‘Join tree’ only for join requests and c) a ‘Main tree’ using several Skinny trees only for leave requests. It uses the residency time of users and it makes sure that the location of both join and leave members are close to the root of the main tree in order to reduce the rekeying cost.

The methods proposed in [17, 18, 20-24] use binary key tree and the methods [17-19, 22-24] use computationally expensive DH algorithm which are not suitable for CRMANETs. In the above discussed protocols, the joining users should wait until either the join tree becomes full [23, 24] or the total joining users become power of 3 as in the Ternary Tree Based Method [TTBM]. Hence, these existing protocols cannot be applied in CRMANETs with frequent and dynamic membership changes.

ECDH protocol is quite suited for resource constrained smaller devices in wireless networks rather than DH [25].

In this paper, ECDH based GDH.2 (GECDH.2) is used to compute the group key.

Therefore, a Ternary tree based GECDH.2 (TGECDH.2) protocol which uses BR without any restriction on group size is proposed in this paper. TGECDH.2 uses GECDH.2 for computing the group key and ternary tree is used to reduce the rekeying cost further.

• III.    Ternary Tree-Based Gecdh.2 Protocol (Tgecdh.2)

This section discusses the BR algorithms used in the proposed TGECDH.2 protocol for updating the group key during the membership change in CRNs.

The performance of a rekeying scheme depends on the structure of the key tree. Ternary tree can reduce the total number of rounds and therefore the binary tree is not an efficient data structure for batch rekeying. In [26], Li et al. showed that the balanced ternary tree is the optimal key tree when the group size is a power of 3. Also, the ternary tree is an optimal balanced key tree for the arbitrary group size in batch updates [26].

This proposed protocol TGECDH.2 replaces the binary key tree used in existing methods with a ternary key tree. To reduce the operations involved in the key tree, TGECDH.2 creates a temporary key tree, only when joining members are greater than leaving members. Thus TGECDH.2 reduces the overall complexity involved in rekeying operations.

• A.    Initial Group Key Computation

TGECDH.2 adopts TGDH for constructing the key tree. The rightmost shallowest node is considered as a sponsor. Initial group size ‘n’ can be any positive integer. Computation of initial group key for the group with 9 SUs is shown in Fig.1. The group key is computed in a bottom-up fashion. Each set of three SUs forms a separate subgroup and they use 3-party GECDH.2 protocol to compute a Sub Group key (SG). After calculating the SG, each sponsor of a subgroup broadcasts it to the next subgroup. Finally, the sponsor of the whole group calculates the final Group key (G) and broadcasts the blinded keys to other SUs. This G is used to encrypt and decrypt the data and thus the secure communication can be achieved between SUs in the group.

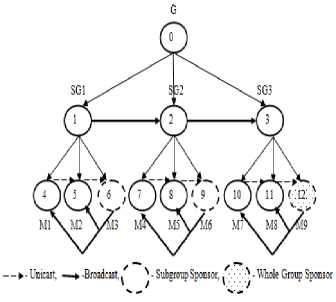
Fig.1. Initial group key computation

• B.    Interval-based BR Method

The BR methods in [22-24] insert the new members into a temporary tree upon receiving the join requests during the current rekeying interval. Unlike these methods, the TGECDH.2 protocol creates the temporary tree only when it is required.

TGECDH.2 works with the following assumptions:

• •    Both SUs and PUs can access the band simultaneously within a licensed spectrum using the U nderlay approach.

• •    A strong digital signature method is used to prevent access to the messages from eavesdroppers.

TGECDH.2 maintains two ternary logical key trees such as a Main Key Tree (MKT) for the current group members and a Temporary Key Tree (TKT) for the joining SUs. It also maintains a queue to store the newly arrived joining SUs. Depending on the variations in the join and leave events, the TKT is created if necessary at the end of the current rekey interval.

The proposed TGECDH.2 protocol uses three algorithms, namely, Ternary_Batch_ Process (TBP), Ternary_Batch_Merge (TBM) and Ternary_Join_Tree (TJT) and these algorithms are given in Alg.1, Alg.2 and Alg.3 respectively.

TGECDH.2 consists of two phases such as Preprocess and Merge. In Preprocess phase, all join and leave requests received during the current rekeying interval are stored in the queue. At the end of the current rekeying interval, the total number of join requests or members (J) is compared with the total number of leave requests or members (L).

In the Merge phase, the TBM algorithm inserts the created TKT at the chosen IP. Then the sponsor computes the updated group key and it broadcasts the updated blinded keys of the nodes in its key path. Upon receiving this message, the other SUs in the group compute the new group key. The abbreviations used in the proposed three algorithms are:

Shallowest Intermediate Node (SIN), New Intermediate Node (NIN), Left Child (LC), Middle Child (MC) and list of New Members (NM).

Fig.2 illustrates the insertion of TKT into MKT during the Merge phase. Since the root is full, the TBP algorithm tries to find the SIN with NULL link. As middle SIN has NULL link, it is selected as IP and TKT is inserted here. While choosing the IP, TBP selects the appropriate one, such that it maintains the balanced key tree that helps in reducing the overall rekeying cost. The new sponsor M19 will compute the new group key and it will broadcast the updated blinded keys of the nodes in its key path.

When the total number of join members is equal to the total number of leaving members, Case 2 in TBP algorithm will replace all the leaving members with the joining members. It maintains the association between J and L. TBP starts the replacement from the lowest level of the key tree in the left to right direction. The replacement of L with J is shown in Fig.3. The leaving members M1, M3, M8 and M11 are replaced by the four joining members M15, M16, M13 and M14 respectively. Then the sponsors M2, M9 and M12 re-compute the newgroup key and it will be stored in the root of the key tree.

A lgorithm 1. T ernary _B atch _P rocess

Ternary_Batch_Process (MKT, J, L)

{

• Case 1:    (Joins with no leave members)

{ if (J>L and L==0) then

{

Create a TKT and find IP as follows if (Root is full) then

{         if (any of the SIN has null link) then

IP=SIN with less ID.

else

IP= SIN with minimum height.

If (insertion at IP increases the height of the MKT) then IP= Root node.

} else

{IP=Root node.}

}

}

• Case 2:    (Joins with leave members)

{ if (L >0) then

{ free= ID’s of leaving members.

if (leaving node ‘n a ’ && all its siblings are in ‘free’) then free= (free\ { n a, n b } or { n a, n b, n c }) U parent (n a ).

Sort the set ‘free’.

if (J == L) then

Replace L with J and mark the nodes to be updated.

else if (J < L) then

{

Select first ‘J’ positions from ‘free’ and replace L with J.

Remove remaining leaving members and mark the nodes to be updated. } else if (L>J and J==0) then

Remove all leaving members and mark the nodes to be updated.

else

{

Insert ‘L’ joining members in the locations of ‘L’ leaving members.

Create TKT with remaining ‘J-L’ joining members.

Find IP as in Case 1.

}

}

}

}

A lgorithm 2. T ernary B atch M erge

Ternary_Batch_Merge (MKT, TKT, IP)

{           if (IP has null link) then

Insert TKT as its child node and mark the nodes to be updated.

else

{

Create a NIN and LC (NIN) = member at IP.

MC (NIN) = TKT.

Mark the nodes to be updated.

}

Sponsor re-computes the new group key and broadcasts the new blinded keys.

Other members compute the new group key.

}

A lgorithm 3. T ernary _J oin _T ree

Ternary_Join _Tree (N, NM)

{ if (N is power of 3)

Form subgroups of three members and merge them by finding the IP until there is no subgroup. else

{

Form subgroups of three members and form a last subgroup with the remaining members.

Merge them by finding the IP until there is no subgroup.

}

Sponsor re-computes the new group key and broadcasts the new blinded keys.

Other members compute the new group key.

}

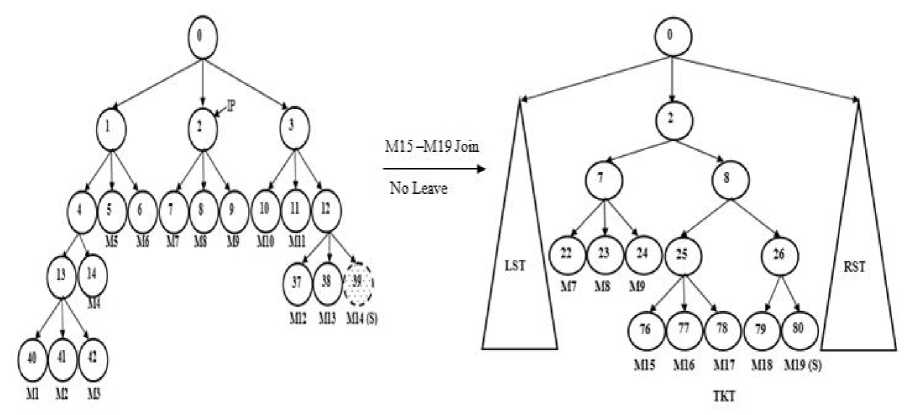
Fig.2. Merging of created TKT with MKT during Batch Rekeying

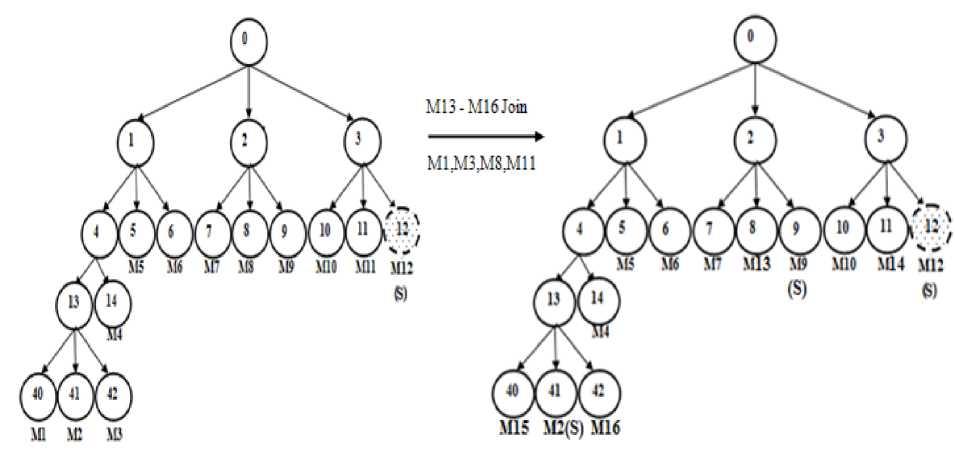
Fig.3 Replacement of leaving members with joining members during Batch Rekeying

Iv. Performance Analysis

This section compares the performance of the proposed TGECDH.2 protocol with existing IR based TTBM. The metrics such as the initial group key generation time and rekeying time are used to analyze the computational complexity, whereas the number of renewed nodes indicates the communication complexity. In Fig.4, Fig.5 and Fig.6, the group size is represented in the x-axis whereas initial group key generation time and the number of renewed nodes are indicated in the y-axis. The difference in initial group key generation time between TGECDH.2 and TTBM is shown in Fig.4. As TGECDH.2 uses ECDH protocol in GDH.2, it reduces the time for generating the initial group key for the initial group members. TTBM restricts the group size and it should be a power of 3. But TGECDH.2 can create a group for any number of members. Fig.4 shows that a group key for the group with 300 members was generated in TGECDH.2 and the same group was not accepted in TTBM.

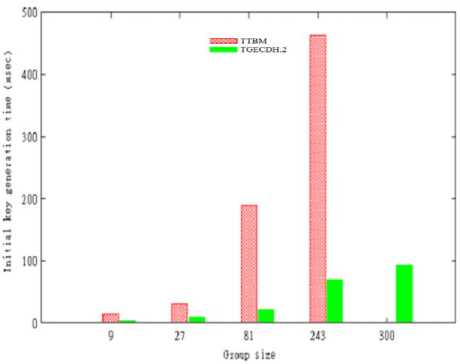
Fig.4. Performance comparison based on initial key generation time.

The different values for join and leave were considered and the total number of renewed nodes was measured for different group sizes during rekeying operation. The BR mechanism was not employed in TTBM. The new members were inserted in the main key tree one by one and the leaving members were allowed to leave from the group one at a time. This increased the number of times rekeying is to be done and also the total number of modular exponentiations. Fig.5 depicts the performance difference between these two methods in terms of total number of renewed nodes.

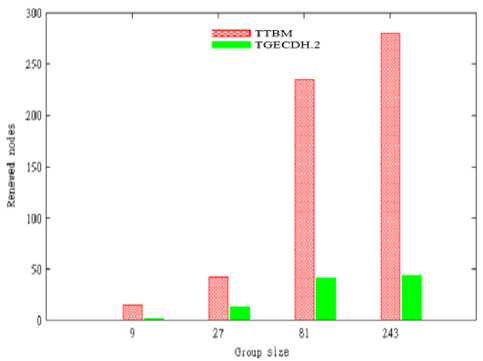
Fig.5. Comparison of renewed nodes among TGECDH.2 and TTBM

Fig.5 illustrates that TGECDH.2 has less number of renewed nodes when compared to the existing method TTBM. Less than 50 nodes were generated even in a large group with 35 (243) members. But, more than 250 renewed nodes were generated for the group with the same size in TTBM. This is due to individual rekeying operations.

The number of joining members was varied for a constant number of leaving members, and the total number of renewed nodes was measured. Fig.6 represents the variations in the number of renewed nodes for different number of joining members. Here, the total number of leaving members considered was 34 (81) and the total number of members joining the group at different point of time was considered to be 3i, for 0≤ i≤4.

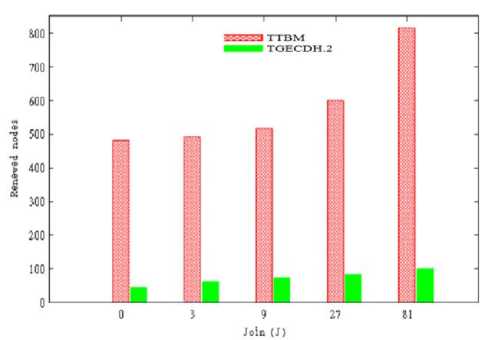
Fig.6 Number of renewed nodes at different joins with fixed leave.

The number of renewed nodes is high in TTBM when compared to TGECDH.2 as shown in Fig. 6. There is only a slight increment in the number of renewed nodes in TGECDH.2 when the group size is increased.

In Fig.7 and Fig.8, the x-axis shows the total number of joining members (J), while the y-axis represents the total number of leaving members (L). The z axis indicates the measured rekeying time and total number of renewed nodes calculated during BR process. A group with 35 (243) members was considered at the beginning of each observation. The test cases with different values of join and leave members were considered.

Fig.7 and Fig.8 compare the performance of TGECDH.2 and TTBM during the rekeying process. The different values for leave were considered by keeping the join value as constant and vice versa. The time for generating the new group keys and the number of renewed nodes were measured.

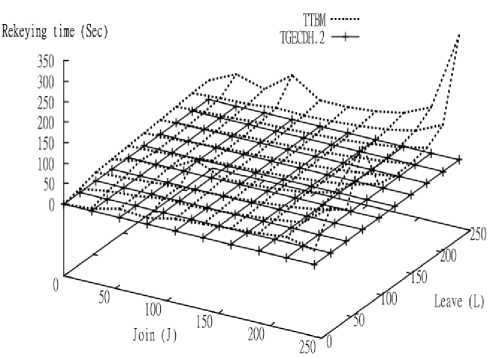
Fig.7. Performance comparison based on rekeying time

Fig.7 shows that the TGECDH.2 requires less rekeying time than TTBM for generating the new group key. The rekeying time of TTBM is increased when the group size is increased. From the graph, it is inferred that even for a large value of J and L, the rekeying time in TGECDH.2 is less when compared to IR method TTBM.

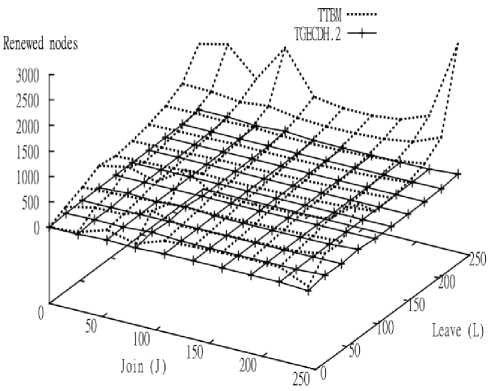
Fig.8. Performance comparison based on number of renewed nodes.

The number of renewed nodes is also less in TGECDH.2 when compared to TTBM as shown in Fig.8. The total number of renewed nodes for large value of J and L in IR method is greater than the value obtained in TGECDH.2.

From the above graphs, it is inferred that the proposed TGECDH.2 protocol outperforms TTBM, as TGECDH.2 uses ECDH rather than DH and it pre-processes Js and Ls using its BR approach. Further, the rekeying cost depends on the structure of the key tree and the TBP algorithm always tries to maintain the balanced key tree by finding the appropriate IP where the height of the key tree is not increased. It is clear from the performance analysis that, there is a significant reduction both in computation and communication cost when the values for J and L are large, i.e., in dynamic group. Based on the obtained results, it can be inferred that the TGECDH.2 performs better and reduces both computational and communication complexity compared to TTBM. Therefore, TGECDH.2 protocol is suitable for small devices with less battery power in CRMANETs.

• V. Conclusion

The proposed CGKA protocol TGECDH.2 reduces both computational and communication complexity in group key agreement for secure communication between CR users. The TGECDH.2 protocol is best suited for highly dynamic groups with frequent membership changes in resource restricted CRMANETs. Hence, this protocol can be applied to portable mobile devices such as tablet PCs, smart phones, pocket size PCs used in several applications such as video conferences, virtual classrooms, etc.