Тестирование спектра Учайкина - Золотарева по данным для межзвездной среды

В современных исследованиях межзвездной среды широко применяются модели турбулентности из магнитогидродинамики (далее – МГД), которые учитывают взаимодействие магнитных полей и плазмы, что играет решающую роль формировании структуры межзвездной среды. Использование спектров мощности в данных исследованиях является ключевым аспектом, который позволяет лучше понять процессы передачи энергии в различных масштабах, поэтому с зарождения теории спектров мощности турбулентных потоков в работах А.Н. Колмогорова и его гипотезы энергетического каскада [1; 2] они стали неотъемлемой частью анализа турбулентных явлений и широко применяются в различных областях физики, метеорологии, гидродинамики и других дисциплин.

Данная работа является продолжением серии статей, посвященных аппроксимированию спектров мощности [3; 4], в которой проводится сравнительный анализ аппроксимаций спектров мощности со спектром мощности Учайкина – Золотарева.

*Автор выражает благодарность своему научному руководителю Учайкину В.В. за помощь с подбором темы, изучением материалов, проверкой результатов, а также с написанием данной статьи.

Кожемякин Илья Игоревич аспирант, Ульяновский государственный университет, город Ульяновск. Сфера научных интересов: математическое моделирование, астрофизика, информационные технологии. Автор 11 опубликованных научных работ. ORCID: 0000-0001-9585-2625, Scopus Author ID: 57221482784, SPIN-код: 1795-2219, AuthorID: 1246499.

Аппроксимации спектра мощности

Гипотеза энергетического каскада, предложенная Колмогоровым, объясняет процесс передачи энергии от крупномасштабных турбулентных движений к мелкомасштабным турбулентным движениям в жидкостях или газах. Колмогоров предположил, что энергия передается через каскадный процесс, где более крупные вихри переносят энергию на более мелкие масштабы путем последовательного распада.

Классическим подходом к анализу спектра мощности турбулентности является спектр мощности Колмогорова . В его гипотезе описывается принцип передачи энергии от низких волновых чисел к высоким волновым числам, называемый энергетическим каскадом . В промежуточном диапазоне масштабов, так называемом инерционном интервале , диапазон масштабов длин статистически изотропен, и его характеристики в равновесии будут зависеть только от скорости, а гипотеза Колмогорова приводит к следующей универсальной форме энергетического спектра

' . р. ( k ) = Ak ° , (1) и в классической форме принимается а = - 5 / 3 .

Несмотря на то что эта форма спектра используется повсеместно ввиду своей простоты, инерционный интервал является лишь одним из трех интервалов, на которые спектр турбулентности параметрически и визуально раскладывается в гипотезе энергетического каскада, как показано на Рисунке 1 [5].

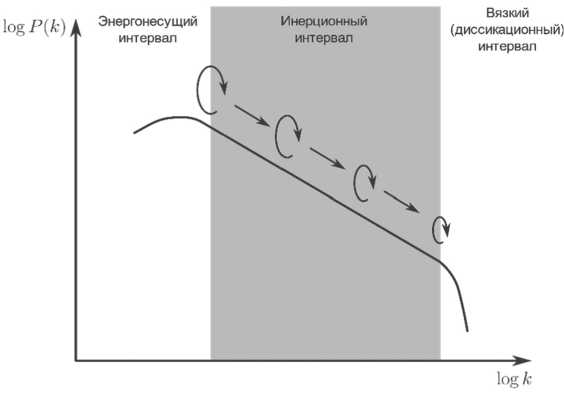
Рисунок 1. Условная схема энергетического каскада Источник: рисунок выполнен автором на основе [5].

Тестирование спектра Учайкина – Золотарева по данным для межзвездной среды

Помимо инерционного, в спектре различают энергонесущий интервал, что соответ- ствует малым волновым числам k и характеризует самые большие движения или вихри турбулентности, содержащие большую часть кинетической энергии, и вязкий интервал

(или диссипационный ), который соответствует большим k , характеризует наименьшие вихри, ответственные за вязкую диссипацию кинетической энергии турбулентности, в процессе которого происходит преобразование механической энергии в тепловую из-за воздействий сил трения.

Поскольку колмогоровский спектр не может учитывать некоторые аспекты, такие как анизотропия, влияние вязкости и в случае МГД-систем – магнитные поля, которые могут оказать существенное влияние на энергетический каскад, данная аппроксимация не предоставляет полной картины взаимодействия между масштабами и процессами передачи энергии в турбулентности. Это открыло необходимость в создании более комплексных аппроксимаций, которые могли быть дать более полную картину.

Например, вскоре после возникновения гипотезы Колмогорова был предложен спектр фон Кармана [6] как модификация спектра Колмогорова (1) для уточнения формы спектра Колмогорова в энергонесущем интервале:

ôон Êарìан

(k ) = A

k

a

[ 1 + ( k / k e ) ² ]

( a + в ) /2

в оригинальной работе использовались значения a = 4, a + в = 17/6, k e = 1.

Данный спектр отличается от колмогоровского только в энергонесущем интервале,

асимптотически сравниваясь с ним в вязком.

Другой спектр, получивший название логнормальный , был предложен в статьях Ли [7; 8] и описывает распределение энергии, которое максимизирует энтропию Шеннона и имеет вид

C 2

Логнормальный ( k ) = 4exp | ^- ( ^ - log k ) ( ^C 2 ^{+ C} 3 k 2 ) } ,                  ⁽³⁾

k где C1 , C2 , C3 – параметры метода множителей Лагранжа, использованного при решении.

Мезофрактальная модель. Спектр Учайкина – Золотарева

Колмогоровская феноменология турбулентности с ее автомодельными степенными законами была прообразом фрактальной концепции Мандельброта, которая нашла применение и в вопросах изучения межзвездной среды и стала необычайно популярной в конце минувшего века [9]. Однако чистая фрактальная теория имела некоторые ограничения, связанные в первую очередь с тем, что изучаемые распределения не являются полным фракталами: в определенный момент, когда масштаб становится слишком мелким, распределение теряет фрактальные свойства, сначала просто меняя свою фрактальную размерность, а на особо мелких масштабах становясь однородным. С учетом этих особенностей были сформулированы две производные модели: мультифрактальная и мезофрак-тальная [10; 11], являющаяся моделью, в которой функционирует исследуемая в данной статье аппроксимация.

В своей основе мезофрактальная модель использует известное уравнение статистической механики, которое позволяет рассчитать корреляцию плотности между двумя точками, – обобщенное уравнение Орнштейна – Цернике [12]:

^(x) = Ab 3p(x/b;a) + cb 3 Jp(x/b)^(x-x')dx',

в котором в качестве начальных узлов марковских траекторий принято однородное пуассоновское распределение бесконечного множества точек, а прямой корреляционной функции p ( x / b ) соответствует собственная функция нелокального оператора дробного лапласиана д ^а /2 . Решение такого уравнения представляется в виде фурье-образа двухточечной корреляционной функции как

- - ( ^bk ) "

P (k) = A ----------,

^узу ’      1      - ( bk )^а

1 - ce у ’ которое называется спектр Учайкина – Золотарева (далее – УЗ).

Полезной особенностью спектра УЗ является его разделение на три интервала энергетического каскада, предложенных в теории Колмогорова (см. Рисунок 1), что проиллюстрировано на Рисунке 2.

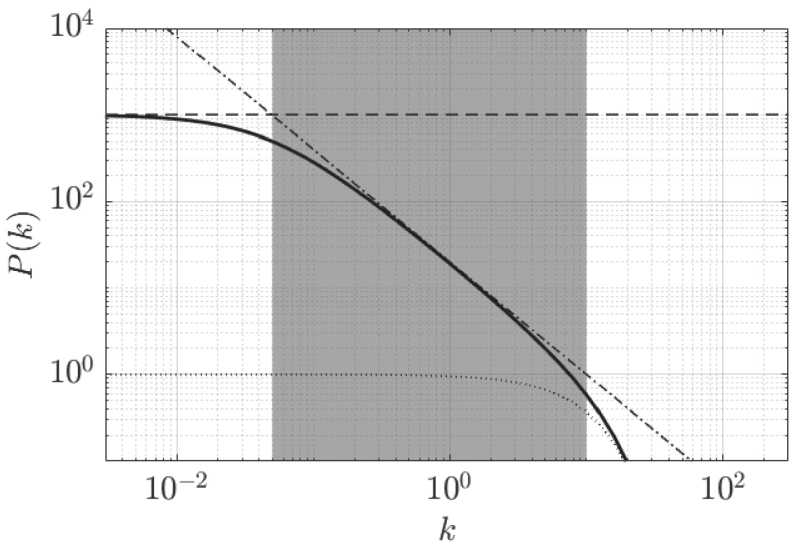
Рисунок 2. Пример спектра Учайкина – Золотарева (5) и его асимптотики на разных интервалах энергетического каскада: сплошная линия – пример спектра для параметров a = 1,3; b = 10 1 ; c = 1 —10 ³ ; A = 1 ; серая область - примерная область инерционного интервала, соответствующая k е ( k 1 , k 2 ) ; штриховая линия - асимптота спектра в энергонесущем интервале (7); штрих-пунктирная линия – асимптотика спектра в инерционном интервале (8); пунктирная линия – асимптотика спектра в вязком интервале (9)

Источник: здесь и далее рисунки выполнены автором.

Проанализировав нули второй производной логарифма спектра УЗ (5), получим границы инерционного интервала:

k 1 - b -¹ ( 1 - c ) ^а , Р уз ( k 1 ) = -A -,

1 - c k2 - b-1,        Руз (k2 ) = A, где k1 – граница с энергонесущим интервалом; k2 – граница с диссипационным интервалом.

Тестирование спектра Учайкина – Золотарева по данным для межзвездной среды

Энергонесущий интервал соответствует малым k и большим движениям и вихрям турбулентности, в асимптоте k ^ 0 принимает значение постоянной:

A lim Р о ( k ) =----= const .

к^о уз^ >1

Вязкий интервал соответствует большим k и наименьшим завихрениям, и спектр уходит в асимптотику экспоненциального вида lim P(к)® Ae-(bk)а.

к ^ю

Наконец, в инерционном интервале, соответствующем средним значениям волнового числа к е ( к 1 , к 2 ) , спектр приблизительно соответствует колмогоровскому спектру:

Руз (к) = ( Ab-а) к-а.(9)

Таким образом, можно сформулировать механический смысл параметров спектра УЗ:

• •    а - параметр колмогоровского спектра в инерционном интервале;

• •    A – энергия, на которой начинается диссипация турбулентности;

• •    b – размер волны (так как это обратное значение к k ), на котором начинается диссипация турбулентности;

• •    c – параметр, указывающий, во сколько раз уменьшается энергия в инерционном интервале.

Оценка аппроксимаций

Для оценки аппроксимаций предлагается использовать методы регрессионного анализа для минимизации оценочной функции среднеквадратичной логарифмической ошибки (далее – СКЛО):

^ СКЛО = n Z^ n ^Р ( ^ki )^- ln P i' ] 2 ’                          ⁽¹⁰⁾

i где Pi - значение исходного спектра для волнового числа к;-; Р (к^) - спектр, которым аппроксимируется исходный спектр.

Выбор логарифмической ошибки вместо наиболее используемой линейной мотивирован природой спектров мощности: будучи преобразованиями Фурье, имеющими экспоненциальную природу, графики спектров мощности всегда строятся на дважды логарифмических масштабах, показывая, что в процессе турбулентности кинетическая энергия может падать на несколько порядков.

У всех сравниваемых спектров есть параметр, который математически является коэффициентом пропорциональности; для логнормального спектра таким параметром является C ₁ , для всех остальных – A . Особенностью подобного параметра является возможность исключения его при регрессионном поиске параметров с минимизацией среднеквадратичной ошибки (как линейной, так и логарифмической). Для этого достаточно показать, что если разложить исследуемый спектр как Р ( к ) = A p ( к ) и представить СКЛО (10) как функцию от такого параметра A , то вычисление ошибки может быть упрощено:

Г      „^M²

^ скло

⁽ A ^^Dn ( Ap ⁽ M-ln P i ] = “E ln A ⁺ ln^ nnP

—^ = n 3> A + In й! =

i

P i

= П Е^{( ln} A ^{) 2} + 2 Е ^ln A ^ln Q ⁺E ( ^ln Q ) = _ i                         i                          i

= ( ^ln A ) ^{2 +} n^ln A 5 ln Q i⁺ ^ ( ln Q i )².

i                    i

Поскольку все переменные внутри Q предопределены и не зависят от A , можно оставить его вычисление вне этого процесса и считать его постоянным для данного рассуждения. Выражение (11) имеет параболическую форму со строго положительным параметром перед квадратичным членом, так что для него существует ровно одна точка, в которой СКЛО достигает минимума:

min In A =

, У, ^ln Q i ^ A скло 2 n

z

= min A = exp

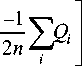
Таким образом, вычисление СКЛО производится по следующему алгоритму:

P ^{( k}i )

• 1.    Вычисляем для всех i значения Qi =       .

• 2.    На основе полученных значений вычисляем суммы 5 In Q i и 5 ( In Q i ) .

• 3.    Находим значение A _скло , используя вычисление (12), в которой будет достигнут

• 4.    Подставляем полученные значения в выражение (11), чтобы найти итоговое значе-

• ние ^скло.

i ₂

ii

минимум СКЛО.

Используя эту функцию в качестве оценочной, можно применять методы регрессионного анализа для поиска параметров спектров мощности, при которых СКЛО с оценочной функцией будет минимальной.

В представленной статье для данного процесса используется симплексный метод Нелдера – Мида [13] для набора точек, распределенных равномерно в широком диапазоне пространства К ^{k - 1} , где к - количество параметров для исследуемой аппроксимации, при этом, уменьшая размерность на один, необходимо учитывать, что один из параметров вынесен из процесса регрессионного анализа, как показано выше.

Результаты

На Рисунке 3 и в Таблице представлены результаты аппроксимаций некоторых спектров мощности с использованием аппроксимаций, представленных выше.

На Рисунке 3 а представлена аппроксимация спектра, представленного в работе [14]. В данной работе исследовалась численно сгенерированная трехмерная МГД-турбулентность с использованием МГД-кода и варьирования входных значений звукового и альвеновского чисел Маха. Представлен случай с меньшим числом Альвена – Маха и толстым корпусом с переменным содержанием.

Тестирование спектра Учайкина – Золотарева по данным для межзвездной среды

На Рисунке 3 б аппроксимирован спектр, представленный в работе [15], где интерпретируются результаты, полученные в статье [16] с использованием гибридного метода решения идеальных изотермических уравнений МГД в периодическом ящике. В последующей статье [15] производился расчет сжимаемой МГД-турбулентности с третьим порядком точности с использованием гибридного существенно неколебательного решения идеальных изотермических уравнений МГД.

На Рисунке 3 в аппроксимирован спектр, представленный в работе [17], в которой производилось исследование распространения сильных ударных волн в двухфазной среде с использованием схемы Годунова второго порядка для решения уравнений МГД.

На Рисунке 3 г аппроксимирован спектр из работы [18]. Здесь авторы продолжают исследование по изучению диффузионного ударного ускорения в остатках сверхновых RX J1713.7-3946, рассматривая этот процесс как трехмерное МГД-моделирование ударной волны, взаимодействующей с межзвездными облаками.

На Рисунке 3 д аппроксимирован спектр энергии из работы [19], в которой изучаются статистика и масштабирование скорости, давления и плотности в сжимаемой турбулентности, в поле течения которого присутствуют крупномасштабные ударные структуры и трубчатые вихревые структуры. Аппроксимированный спектр кинетической энергии демонстрирует масштабное поведение в инерционном диапазоне.

На Рисунке 3 е аппроксимирован спектр, представленный в работе [20], где изучаются пространственно-усредненные спектры мощности по данным из системы обработки астрономических изображений NRAO AIPS. Аппроксимированный спектр является расчетным спектром в фазе теплой нейтральной среды.

Таблица

Значения ^ скло Для аппроксимаций разных исходных спектров и соответствующих аппроксимаций

Исходный спектр	Аппроксимирующий спектр
	Колмогорова	фон Кармана	логнормальный	УЗ
(а)	1,8291	1,8291	0,043737	0,010049
(б)	0,27905	0,13514	0,24802	0,017519
(в)	0,16846	0,057985	0,14685	0,019763
(г)	0,034753	0,0030914	0,028806	0,00085899
(д)	0,089469	0,0037637	0,0077488	0,00032568
(е)	2,6041	2,6041	0,056634	0,041652

Источник: таблица составлена автором.

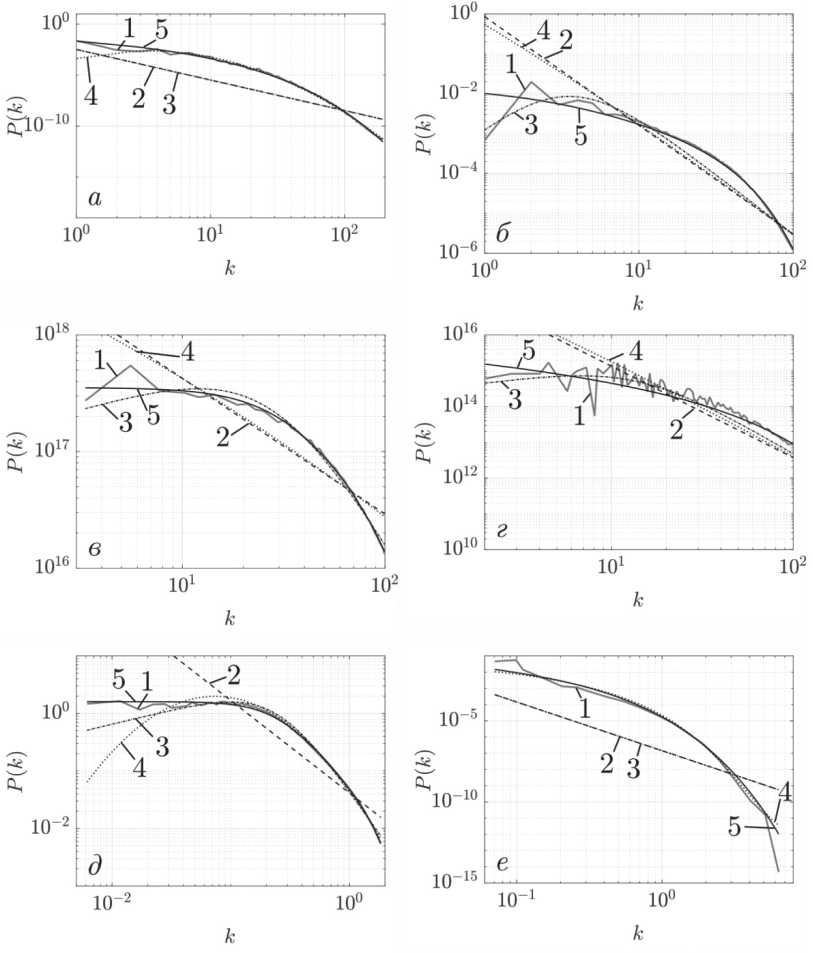
Рисунок 3. Графики аппроксимаций различными спектрами мощности: линия 1 иллюстрирует исходный спектр мощности (источники указаны в тексте статьи); штриховая линия 2 соответствует аппроксимации спектром Колмогорова (1); штрихпунктирная линия 3 – спектром фон Кармана (2); пунктирная линия 4 – логнормальным спектром Ли (3); линия 5 – спектром Учайкина – Золотарева (5).

Источник: рисунок выполнен автором на основе данных [13; 14; 16; 17; 18; 19].

Обсуждение

На данных рисунках представлены не все примеры аппроксимаций спектров, однако они достаточно полно демонстрируют особенности, с которыми можно столкнуться при аппроксимации спектров мощности турбулентности.

Тестирование спектра Учайкина – Золотарева по данным для межзвездной среды

Так, например, спектр Колмогорова является самой простой аппроксимаций, и для корректной аппроксимации требуется отсечь из аппроксимируемой области энергоне-сущий и вязкий интервалы, для которых колмогоровский спектр не определяется. Если этого не сделать, то значение СКЛО становится больше на несколько порядков.

Также наблюдается высокая нестабильность аппроксимации логнормальным спектром (3). Для некоторых спектров (например, см. Рисунок 3 а ) данный спектр аппроксимирует представленные спектры адекватно. При детальном изучении линий становится ясно, что данная аппроксимация имеет СКЛО, сравнительную с другими аппроксимациями в тех случаях, когда исходный спектр слабо возрастает в энергонесущем интервале, как на Рисунке 3 а или 3 е .

Спектр фон Кармана, с другой стороны, стабильнее реагирует на флуктуации в энер-гонесущем диапазоне, однако из-за степенной природы спектра СКЛО аппроксимации становится больше на несколько порядков, если у исходного спектра присутствует ярко выраженный вязкий интервал, например, как на Рисунке 3 б .

Спектр Учайкина – Золотарева в данном цикле аппроксимаций показал себя лучше остальных аппроксимаций: значение СКЛО для всех исходных спектров ниже, чем у других спектров. Такая универсальность показывает, что использование спектра мощности Учайкина – Золотарева является весьма эффективной аппроксимацией для широкого ряда спектров, которая позволяет аппроксимировать большое количество спектров с хорошей точностью в автоматическом режиме. Например, для параметров спектра Учайкина – Золотарева можно установить связи с параметрами кластеризации среды. Подобные исследования активно проводились для вопросов распределения галактик [21; 22], в которых данный спектр также применим.

Дополнительно стоит отметить, что до сих пор наши исследования были связаны со спектрами несжимаемой турбулентности, однако, как показано на Рисунке 3 д , спектр сжимаемой турбулентности также аппроксимируется спектром Учайкина – Золотарева, но потребуются дополнительная работа по изучению формирования сжимаемой турбулентности и уместности применения методов несжимаемой турбулентности.

Заключение

В целом проведенное исследование показывает, что спектр мощности Учайкина – Золотарева является весьма эффективной аппроксимацией, которая позволяет аппроксимировать большое количество спектров с хорошей точностью. Дальнейшие исследования могут использовать данную аппроксимацию для получения дополнительной информации об исследуемых моделях. Так, может быть полезным установка связи между параметрами спектра Учайкина – Золотарева и параметрами кластеризации среды.