Тетраэдры с одинаковым набором длин рёбер и объёмом, вписанные в одну сферу

Проблема, распознавания равных симплексов связана, с поиском общих геометрических характеристик, равенство которых позволит доказать изоморфизм симплексов [1]. Естественно в качестве общих характеристик выбирать длины рёбер симплекса. Однако для симплексов в R ³ (тетраэдров) равенство наборов длин рёбер ещё не обеспечивает их конгруэнтность. Другими наиболее естественными геометрическими характеристиками, связанными с тетраэдром, являются радиус описанной сферы п объём. Попытки автора, доказать символьно конгруэнтность тетраэдров с данным набором длин рёбер, объёмом и радиусом описанной сферы не привели к положительному результату, по зато удалось построить контрпример, который приводится в данной работе.

Утверждение. Существуют пекопгруэпт-иые тетраэдры с одинаковым набором длин рёбер и объёмом, вписанные в одну сферу. □

Будем считать, что нам задано конкретное распределение положительных чисел 1i (1 6 i 6 6) по рёбрам тетраэдра, (см. рис. 1).

¹⁴⁴ • V — I 1 • I 5 • ⁽ I 2 + I 6 + I 3 + I 4    I 5    I 1^{) +}

^{+ 1} 2 ¹ 6  ^{( 1} 3 ^{+ 1} 4 ^{+ 1} 1 ^{+ 1} 5    ¹ 2

22   2   2   2   2   2

^{+ 1} 3 ¹ 4  ^{( 1} 1 ^{+ 1} 5 ^{+ 1} 2 ^{+ 1} 6    ¹ 3

где Q —

222 222 22

¹ 1 • ¹ 2 • ¹ 4       ¹ 2 • ¹ 3 • ¹ 5       ¹ 1 • ¹ 3 •

1 1 • I 5 5 + 1 2 • 1 6 + 1 3 • 1 4

1 2)+

l ₆

¹ 4 • ¹ 5 • ¹ 6 ,

Теперь поменяем местами рёбра 1 1 и 1 ₂.

Бу

дем считать, что для рассматриваемых нами распределений соответствующие значения объёмов и радиусов совпадают. В результате такого сопоставления получаются 2 полиномиальные связи на длины рёбер тетраэдра. После упрощения и разложения на множители получается следующая система. уравнений:

( 1 2 - 1 2²) • ( 1 2 - 1 2) х

22 22 22 22   22

х (11 • 15 + 12 • 15 + 11 • 16 + 12 • 16 - 2 • 13 • 14) — 0, (12 -122) • (12 -12) х х (12 +12 +12 +12 -14 - 2 • 12) —о.

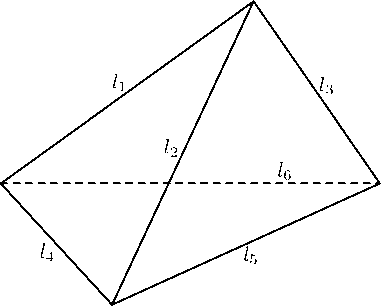
Рис. 1

Выпишем для этого распределения формулы для вычисления объёма ( V ) и радиуса описанной сферы ( R ) [2] и [3]:

36 • V ² • R ² = Q • ( Q - 1 1 • 1 5) • ( Q - 1 2 • 1 б) • ( Q - 1 3 • 1 4) ,

Рассмотрим все варианты совместимости полученной системы уравнений.

1 1 — 1 2 (остальные рёбра произвольны).

Так как именно эти рёбра, менялись местами, то получаются конгруэнтные тетраэдры.

1 5 — 1 6 — с (остальные рёбра произвольны).

В данном случае получаются конгруэнтные тетраэдры (см. рис. 2).

Действительно, у таких тетраэдров есть грань, построенная на отрезках c, с, 1 ₄. Кроме того, у каждого тетраэдра, есть ровно по одной вершине, из которой выходят рёбра 1 1, 1 ₂, 1 ₃. Таким образом, существует движение, переводящее один тетраэдр в другой.

Совместна, следующая система, уравнений:

22 22 22 2222

¹ 1 • ¹ 5 ^{+ 1} 2 • ¹ 5 ^{+ 1} 1 • ¹ 6 ^{+ 1} 2 • ¹ 6 ^{- 2} • ¹ 3 • ¹ 4 ^{— 0} ,

¹ 5 ^{+ 1} 6 ^{+ 1} 1 ^{+ 1} 2 ¹ 4 ² • ¹ 3 ^{— 0} •

Приведём систему к следующему виду:

2   2   2   222

(11 + 12) • (15 + 16) — 2 • 13 • 14, 22  22  22

( 1 ₁ + 1 ₂) + ( 1 ₅ + 1 ₆) — 1 ₄ + 2 • 1 ₃ .

Теперь воспользуемся леммой.

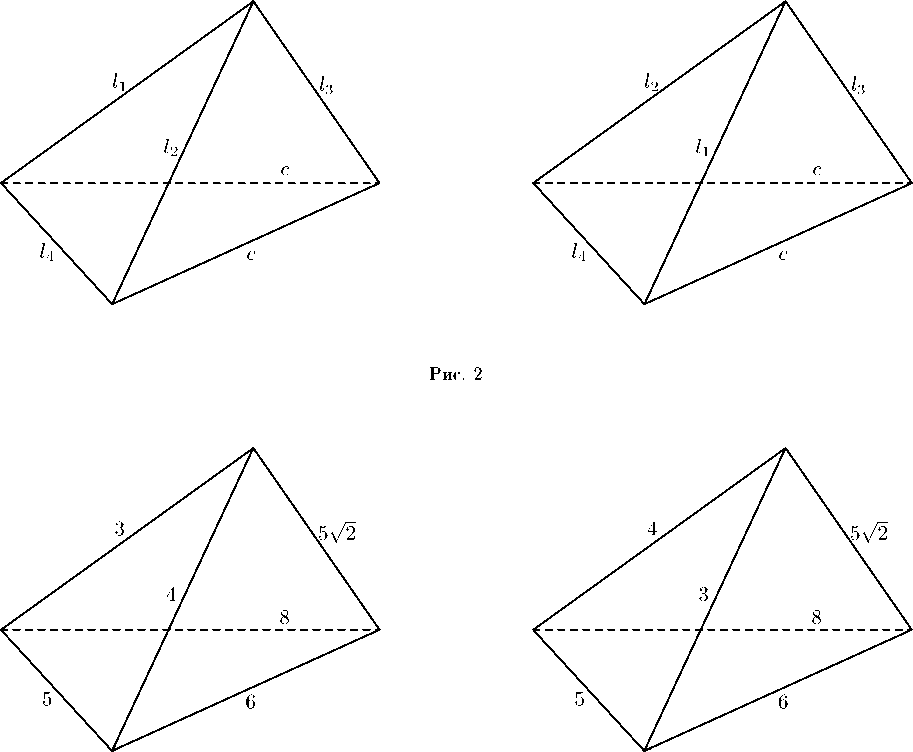
Рис. 3

Лемма. Пусть нам даны числа m, n, p, q, между которыми существует связь:

В заключение приводится вычисленное значе ние объёма, и радиуса, описанной сферы построен-

( m + n = p + q, I m • n = p • q.

пых иекоигруэитиых тетраэдров:

Тогда наборы чисел { m, n } и { p, q } совпадают. □

Доказательство. Действительно, по теореме Виета, эти наборы чисел являются корнями одного и того же квадратного уравнения, поэтому мио-

V =

R =

5 • V203

11 . 873;

5 • V203 • V52?

4 . 028 .

жества. совпадают.

Таким образом, полученная нами система, уравнений имеет две серии решений:

1 2 + 1 2 = 1 2

1 2 + 1 22 = 2 • 1 2

A ( 1 2 + 1 2 = 1 2 \

’      1 2 + 1 2 = 2 • 1 2 .

Возьмём для рассмотрения первое решение (второе решение рассматривается аналогично). Придавая рёбрам l 1, l 2, l 5, l 6 конкретные числовые значения ( l 1 = 3. l 2 = 4. l 5 = 6. l 6 = 8). получаем два. иекоигруэитиых тетраэдра, (см. рис. 3).

Тетраэдры с такими длинами рёбер действи тельно существуют, так как для них выполнены условия реализуемости тетраэдров с данной метрикой п данным комбинаторным строением [4]: выполнение строгого неравенства, треугольника, для граней и положительность квадрата, объёма.