Text Steganography Using Quantum Approach in Regional Language with Revised SSCE

Published Online November 2012 in MECS (http://www. DOI: 10.5815/ijcnis.2012.12.08

• I.    I ntroduction

  Information hiding is the ability to prevent or hidden certain aspects from being accessible to others excluding authentic user. It has many sub disciplines. One of the most important sub disciplines is steganography [2] which is derived from a work by Johannes Trithemus (1462-1516) entitled "Steganographia" and comes from the Greek language defined as "covered writing" [3]. It is an ancient art of hiding information in ways a message is hidden in an innocent-looking cover media so that will

not arouse an eavesdropper’s suspicion. Steganography diverges from cryptography in the sense that where cryptography focuses on keeping the contents of a message secret by encryption technique, steganography focuses on keeping the presence of a message secret [20], [21].

Another form of information hiding is digital watermarking, which is the process that embeds data called a watermark, tag or label into a multimedia object such that watermark can be detected or extracted later to make an assertion about the object. The object may be an image, audio, video or text only [22], [23]. A hidden channel could be defined as a communications channel that transfers some kind of information using a method

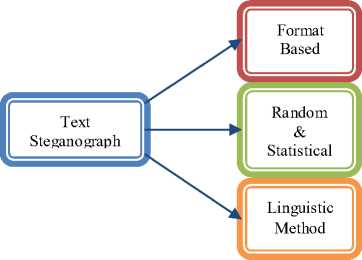
Figure 1: Types of Steganography originally not intended to transfer this kind of information. Observers are unaware that a covert message is being communicated. Only the sender and recipient of the message notice it. Steganography works have been carried out on different media like images, video clips, text, music and sound [24], [21].

In Image Steganography method the secret message is embedded into an image as noise to it, which is nearly impossible to differentiate by human eyes [25], [26], [7]. In video steganography, same method may be used to embed a message [6], [5]. Audio steganography embeds the message into a cover audio file as noise at a frequency out of human hearing range [7]. One major category, perhaps the most difficult kind of steganography is text teganography or linguistic steganography because due to the lack of redundant information in a text compared to an image or audio. The text steganography is a method of using written natural language to conceal a secret message as defined by Chapman et al. [4].

• A.    Quantum Steganography

Comparatively very little research work has been done in quantum steganography also. The idea of hiding secret messages as the error syndromes of a quantum errorcorrecting code (QECC) was introduced by Julio Gea-Banacloche in [28]. In his work Alice and Bob use the three-bit repetition code to transmit messages to each other using a shared secret key. All the noise in the channel that Eve perceives is because of these deliberate errors that Alice applies. In his model he assumes that Alice and Bob share a binary-symmetric channel. This work does not address the issue of whether the errors would resemble a plausible channel, nor does it consider the case where the channel contains intrinsic noise. Natori gives a simple treatment of quantum steganography which is a modification of super-dense coding [29]. Martin introduced a notion of quantum steganographic communication based on a variation of Bennett and Brassard's quantum-key distribution (QKD), hiding a steganographic channel in the QKD protocol [30]. Curty e.al. proposed three different quantum steganographic protocols [31].

• B.    Quantum gate [19]

Quantum circuit model of computation in quantum computing [10] [1] [9], a quantum gate or quantum logic gate is a basic quantum circuit which operates on a small number of qubits. They are the building blocks of quantum circuits, like classical logic gates are basically for conventional digital circuits. Quantum logic gates are reversible like other classical logic gates. However, classical computing can be performed by the help of only reversible gates. Quantum gates are represented as matrices. A gate which acts on k qubits is represented by a 2^kx2^k unitary matrix. The number of qubits in the input and output of the gate is equal. There are various types of quantum gates are represent the qubits. They are Hadamard gate, Pauli-X gate, Pauli-Y gate, Pauli-Z gate, Phase shift gates, Swap gate, Controlled gates, Toffoli gate, Fredkin gate, etc. Here we use Controlled gates to represent the qubits and control the operations.

• C.    Reversible Classical Logic [19]

The first concepts of the reversibility of computation were raised in the 1970s. There were two issues which are logical reversibility and physical reversibility, both were intimately connected. Logical reversibility reconstructs the input from the output of a computation or gate function. The NAND gate is explicitly irreversible, it has two inputs and one output, while the NOT gate is reversible (it’s own inverse). In case of Physical reversibility the NAND gate has only one output, one of it’s inputs has effectively been erased in the process,

whose information has been irretrievably lost. The change in entropy that we would associate with the lost of one bit of information is ln 2, which, thermodynamically, corresponds to an energy increase of kT ln 2, where k is Boltzman’s constant and T is the temperature. The heat dissipated during a process is usually taken to be a sign of physical irreversibility, that the microscopic physical state of the system cannot be restored exactly as it was before the process took place. Reversible logic gates are symmetric with respect to the number of inputs and outputs. The reversible NOT gate, whose truth table is given in Fig. 2. It can also write this in the form of a matrix, or as a graphic. The matrix form lists the lines in the truth table in the form 0 , 1 . t he matrix field with 1's and 0's such that each horizontal or vertical line has exactly one 1, which is to be interpreted as a one-to-one mapping of the input to the output. A two-bit gate closely related to the NOT gate is the two-bit Controlled-NOT (or C-NOT) gate. Controlled-NOT gate shows in Fig. 3, performs a not on the second bit if the first bit is 1 , but otherwise has no effect. The C-NOT is sometimes also called XOR, since it performs an exclusive OR operation on the two inputs bits and writes the output to the second bit.

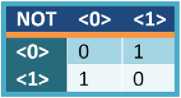
Figure 2: NOT Gate Truth Table

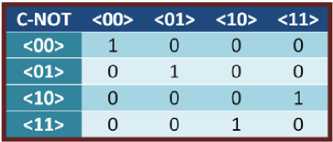
Figure 3: NOT Gate Truth Table

The Controlled NOT gate (also C-NOT or CNOT) is a quantum gate that is an essential component in the construction of a quantum computer. The proof of operation [32] is given below:

Let

basis.

10) =

11=

Let |^) = x|0) + y\1 =

and | ф = y 10) + x| 1 =

x

y

y

x

>

be the orthonormal

| ф be the flip

qubit of | ^ > .

Recall that ^) ® |в = а)в) = |a,в) --(1)

i. When control qubit is 0

First, we shall prove that: CNOT\ 0, ^ ) = 1 0, ^)

Before we compute, however, note that our specific definition of CNOT assumes an eigen basis of

	Г1		"0"		" 0 "		" 0 "
	0				0		0
100) —	0	,l01 —	0	,M—	1	,и—	0
	_ 0 _		_ 0 _		_ 0 _		_ 1 _

Then, it's not difficult to verify

x

that 1 0, ^ ) = x | 0)| 0) + y 0)| 1) =

Then

CNOT\ 0,v) —

x

y

x

y

y

— 10. ,)"

Therefore CNOT doesn't change the | ^ ) qubit if the first qubit is 0.

ii. When control qubit is 1

Now, we shall prove that CNOT | 1, ^ ) — |1 ф ) ,

which means that the CNOT gate flips the | ^ ) qubit.

Similarly have

1^1, ^>

to the

" 0 "

0  .

x

first demonstration, we

y

Then CNOT И -

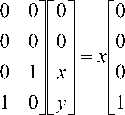
⁺ У

As we can see that 1 1 1) _—

and 1 1,0) —

.. (4)

using these on the equation above gives

CNOT| 1,^) — x | 1,1) + y 1,0) — |1 ( x 1 + y 0) ) — 11, ф - • • (5)

Therefore the CNOT gate flips the | ^ ) qubit into | ф if the control qubit is set to 1. A simple way to observe this is to multiply the CNOT matrix by a column vector, noticing that the operation on the first bit is identity, and a NOT gate on the second bit.

D. Text Steganography

The affluence of electronic documented information available in the world as well as the exertion of serious linguistic analysis makes this an interesting medium for steganographic information hiding. Moreover the Text is one of the ancient media used in steganography. Letters,

books and telegrams hide secret messages within their texts in earlier time i.e. before the electronic age comes. Text steganography refers to the hiding of information within text i.e. character-based messages. There are three basic categories of text steganography (Fig. 1) maintained here: format-based methods, random and statistical generation and linguistic methods. [8]

i. Format-based methods [8]: This methods use the

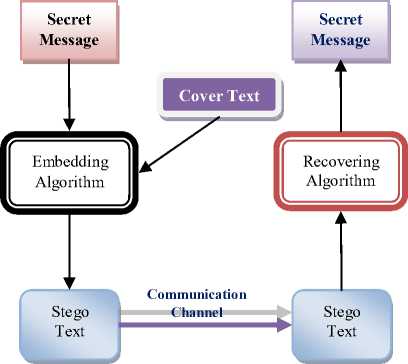
Figure 4: Mechanism of Text Steganography

physical formatting of text as a space in which to hide information. Format-based methods usually modify existing text for hiding the steganographic text. Insertion of spaces or non-displayed characters, careful errors tinny throughout the text and resizing of fonts are some of the many format-based methods used in text steganography.

• ii.    Random and statistical generation method [8]: This avoid comparison with a known plaintext, steganographers often resort to generating their own cover texts. Character sequences method hide the information within character sequences.

• iii.    Linguistic methods [8]: The affluence of electronic documented information available in the world as well as the exertion of serious linguistic analysis makes this an interesting medium for steganographic information hiding.

Fig. 4 shows the mechanism of text steganography. Firstly, a secret message will be covered up in a covertext by applying an embedding algorithm to produce a stego-text. The stego-text will then be transmitted by a communication channel to a receiver.

In this paper, an approach of quantum text steganography using Gujarati character mapping method has been proposed based on the use of some special character. Here the quantum truth table also mapped to increase the security level and complexity. A new code representation method Revised SSCE also has been proposed here to achieve high level of security. Before the embedding operation each character of the secret message has been encoded using Revised SSCE Value and then embeds into cover text by the proposed text steganography method to form the stego text. In this

method the length of the stego and the cover are same so prediction of existence of message is difficult in view of that characteristics, so this one is the unique method which has been developed in this steganography approach.

The proposed scheme has been enthused by the author’s previous work [11], [12], [13], [14], [15], [16], [17], [18] on various approaches of steganography methods. The quantum truth table approach has been incorporated from previous work [18] and The Revised SSCE Value incorporated from SSCE value in [11], [12], [18].

This paper is organized into the following sections. Section II describes the proposed model. Algorithms of various processes like embedding, extracting and GUI are discussed in Section III. Mathematical Analysis furnished in section IV. Analyses of the results are in section V. The last section descries the concluded part of the work.

• II.    T he P roposed M odel

Text steganography, whatever this paper exactly deals with, uses regional language, specifically the Gujarati text

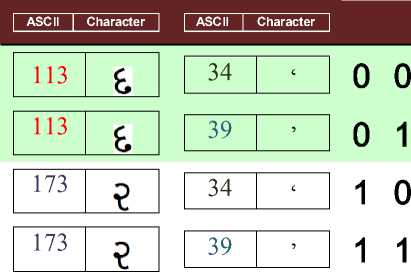
Figure 5: Mapping Technique

as the medium where to hide information. Here the explanation of text steganography remains wide in order to differentiate it from the more specific “linguistic steganography”. Text steganography can involve anything from changing the ASCII character from the specific position of an existing text.

<00*

<01>

1	32	Н^	59	117	69	120		105	115	65	32	6®
154	V	69	107	32	32	107	112	125	65	39	НО	113
35 ,	Л15	107	1	77		69	85	32	93	97	166	32
118	но	1	на	^	34	105	115	93	32	аз	59	100
107	83	107	32	106	НО	32	32	113	65	152	35	125
125	126	115	103	71	93	95	77	32	79	32	126	39
35	107	105	32	93	113	112	172	71	126	49	32	115
44	113	59	118	125	32	119	100	125	39	43	96	100
32	55	32	97	32	33	32	126	101	121	43	121	32
50	115	95	32	112	118	117	32	32	32	32	125	112
53	55	151	95	153	103	93	103	71	НО	32	97	154
32	113	32	121	55	32	100	164	39	118	152	121	42
79	59	52	125	125	НО	115	77	103	32	32	106	32
95	97	45	32	32	117	55	32	32	89	59	115	55
97	101	43	117	117	77	125	93	112	126	172	32	115
32	115	32	97	105	95	73	126	153	32	103	106	НО
112	95	95	55	112	32	113	32	33	67	115	59	33
на	103	115	115	115	89	44	93	32	120	39	96	126
32	115	107	95	32	126	32	121	32	112	106	32	107
45	55	32	32	117	93	117	НО	100	32	113	107	113

Figure 6: Quantum Truth Table Mapping

• A. Solution Methodology

The proposed system involves two windows i.e. SENDER SIDE and RECEIVER SIDE. The user will be someone who is aware with the process of information hiding and will have adequate knowledge of steganography systems. The user have a duty to select a plain text message from a file, another Gujarati text to be used as the carrier (cover text) and then use the proposed embedding method which will hide the message in the selected cover text and will procedure the stego text. The user at the receiver side should be able to extract the message from the stego text with the help of different reverse process in chronological manner to un-hide the message from the stego text. The GUI of the proposed solution has been shown in Fig. 7.

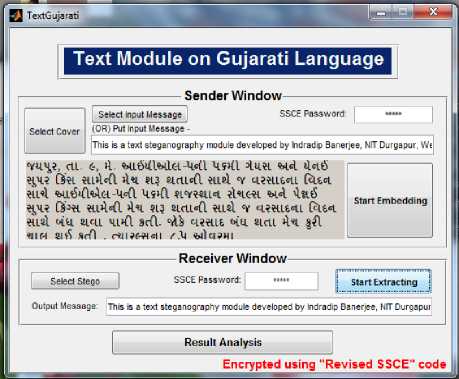
Figure 7: GUI Representation

• III.    Algorithms

In this section, algorithms for different processes used both in the sender side and receiver sides are described which are furnished below:

• A.    Algorithm for Message Encryption / Decryption

• •    Select the Passkey (SSCE Password)

• •    Select the message and pick one by one character.

• •    Convert to its ASCII equivalent.

• •    Change ASCII code to our generated code from SSCE Table (Figure 19) and add Passkey to produced a Revised SSCE value which is depending on Passkey.

• •    Convert to its character equivalent.

• B.    Algorithm for Message Embedding

• •    Select the message and encrypt the message with SSCE value. Then select the Gujarati cover. Check whether the selected text is capable of embedding. If not possible repeat this step otherwise continue.

• •    Map the quantum C-NOT gate to the matrix MATMSG (N x N) vertically or horizontally & Put the message value by replacing ’0’ in the matrix MATMSG.

• •    Check the message sequence and pick first two bit sequence (MSG). Start from the first character of the cover text (TX).

• •    Start checking & embedding.

o If MSG=‘11’ & character “ ” from the TX then change from ASCII (113,246) to (113,39)

o Else If MSG=‘10’ & character “ ” from the TX then change from ASCII (113,246) to (113,34)

o Else If MSG=‘01’ & character “ ” from the TX then change from ASCII (173,247) to (173,39)

o Else If MSG=‘00’ & character “ ” from the TX then change from ASCII (173,247) to (173,34)

• •    Repeat the above step for the remaining bit sequence of the message and prepare the stego text.

• C.    Algorithm for Message Extracting

• •    Select the stego text put in MATMSG (N x N) matrix and map the quantum C-NOT gate to the matrix vertically or horizontally.

• •    Extract the message value from ‘0’Th position of C-NOT. Pick values one by one from MATMSG and create MSG.

• •    Select the stego text TX.

o If “ ” and next ASCII is 39, MSG=’11’.

o Else If “ ” and next ASCII is 34, MSG=’10’.

o Else If “ ” and next ASCII is 39, MSG=’01’.

o Else If “ ” and next ASCII is 34, MSG=’00’.

• D.    Algorithm of GUI in Sender side

• •    Select the Cover Text from the set of Text files.

• •    Check whether the selected text is capable to do the embedding or not. If not possible then error.

• •    Select the message in text form.

• •    Embed the encrypted message in the cover text to form the stego text.

• E.    Algorithm of GUI in Receiver side

• •    Receive the text with embedded message along with positions.

• •    Extract the encrypt form of message from the Stego Text.

• •    Decrypt the message with the help of the previous mentioned SSCE values & Secret key.

• IV.    Mathimatical Analysis

Encryption and Decryption: The entry that lies in the i ^th row and the j ^th column of a matrix is typically referred to as (i, j) ^th entry of a matrix A is most commonly written as A[i, j] or « у.

A [ a i,j ] i=1,2,....,m and j=1,2,....,n

Row and Column operations are ways to change matrices. There are three types of Row operations and three types of column operations, which are furnished below –

Row Operations

• 1.    Interchange row i and j (R i <-- > R j )

• 2.    Multiply row i by s , where s ^ 0 (Ri--> Ri)

• 3.    Add s times row i to row j (_sR j-- > R j ) Column Operations

• 1.    Interchange column i and j (C i <-- > C j )

• 2.    Multiply column i by s , where s + 0 (C i-- > C i )

• 3.    Add s times column i to column j ( _s C j-- > C j ) Now for SSCE value we perform a column operation on matrix A .

After performing a column operation on A[i, j] it produce A ‘ .

A[i, j] - A ’ p, j]

After that transpose the A ' [i, j] matrix and formed A ‘ ^T [i, j] .

Now it is transformed to an array i.e. place in an orderly arrangement in a linear order.

■учу;, cii. 6, 4. ^(ИМы-ч-й 4s41 dma ^4 4ай уч; Ga ^11441 4m ey acudl aid у q;aib«ti Re,«t aid ^dlRa-mdl msdli егеетм ilmc-a mid 4ай уч; G^a ai44l 4m ey aeiidl aid ^ q;aiMi Rm aid dLi ami 4i4l sell Ri q;ai& du adi 4m §;4 I miy ytS sdl . cmi;«idi c .4 «mRini з PGsmi ysei4 кз ;=t ymi| i ^cii mIsyyL ^г1еЛ ад «1^44,$, _ги. 6, 4. здётМы-чч! 4s4l 4чу mi4 4чй уч; Ga ai44l 4m ets ycti4l aid ^ q;aiMi Rm aid i HiSdlmlc-i-mdl 4s4l уумц-ч ;imwi mR 4@uS уч; G=a ai44l 4m ey ycii41 aid "v m;aiMi Rim aid dm yqi 414I sell. Ri q;aiis i du acii 4m §;1 miy atS sell . emiK-aai <.ч Riq^Hl 3 RSmi ysei4 уз ;a ami $eii dsaqi sdell q;aii "vuy;, cti. 6, 4.

• Figure 8: Cover Text

For Revised SSCE value here we add Passkey (known as password) P with A ‘ ^T [i, j] transformed matrix and produced P. A ‘‘ ^T [i, j] .

V. R esults A nalysis

Figure 10: Stego Text

MESSAGE LENGTH (In Character)	CORRELATION VALUE
10	0.99976
50	0.998787621
100	0.997577235
200	0.995159513
300	0.992745838
400	0.990336183
500	0.987930524
600	0.985528835
700	0.983131092
800	0.98073727
900	0.978347344
1000	0.975961289

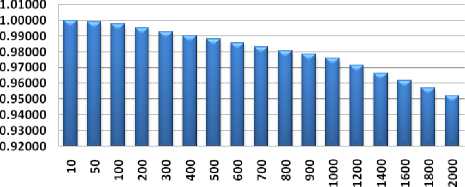
Figure 11: Correlation values of cover and stego text in different length of message

There are mainly three phases that should be reserved into account when discussing the results of the proposed method of text steganography with the help of Gujarati Language. The authors simulated the proposed system and the results are shown in the Fig. 8, 9 and 10. This method satisfies both security aspects and hiding capacity requirements. It generates the stego text with minimum degradation which is not very revealing to people about the existence of any hidden data, maintaining its security to the eavesdroppers. Besides the security level has amplified through the encoding of the secret message before embedding operation. This method hides two bit per word in the cover text which reflects the high embedding capacity of the system. Although the embedding capacity of the proposed method depends upon the embedding sequence, pattern of the cover text. This method hides two bit per word in the cover text which reflects the high embedding capacity of the system. Although the embedding capacity of the proposed method is depends upon the Gujarati characters. In this method the length of the stego and cover are same and unchanged. So due to the said reason the steganalysis part can also handle.

CORRELATION VALUE

Ы CORRELATION VALUE

Figure 12: Representation Correlation values of Cover and Stego

• A. Similarity Measure

For comparing the similarity between cover text and the stego text, the Correlation method for measuring similarity between two strings has been computed. The Correlation [27] is a measure of similarity between two strings.

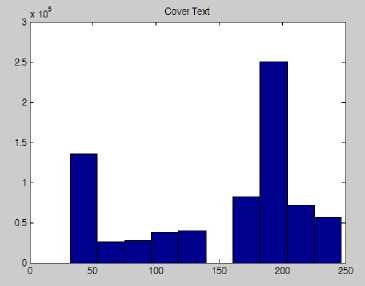
Figure 13: Graph of Cover Text

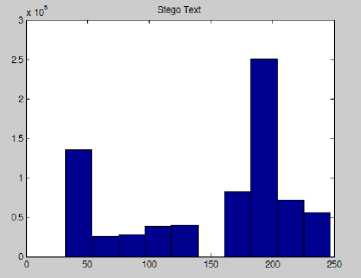
Figure 14: Graph of Stego Text

Correlation : The most familiar measure of dependence between two quantities is the Pearson product-moment correlation coefficient [27], or “Pearson’s correlation”. It

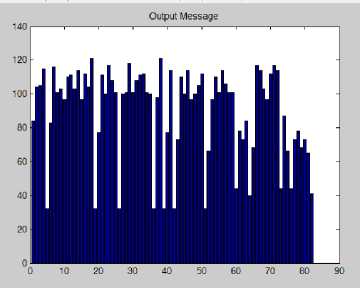
Figure 16: Graph of Output Message

Message Length (In Character)	Computation Time (in Second)
	Stego Generate (A)	Message Generate (B)	Difference (B-A)
10	0.1404009	0.1872012	0.0468003
50	0.6552042	0.6864044	0.0312002
100	1.2168078	1.3572087	0.1404009
200	1.9344124	3.0576196	1.1232072
300	2.7144174	3.3228213	0.6084039
400	3.5724229	4.3836281	0.8112052
500	4.5396291	5.616036	1.0764069
600	5.6940365	7.0512452	1.3572087
700	7.4256476	8.4864544	1.0608068
800	10.4208668	10.8576696	0.4368028
900	9.5784614	10.8888698	1.3104084
1000	9.3288598	11.4192732	2.0904134

Figure 15: Graph of Input Message

is obtained by dividing the covariance of the two variables by the product of their standard deviations. Karl Pearson developed the coefficient from a similar but slightly different idea by Francis Galton. The Pearson correlation is +1 in the case of a perfect positive (increasing) linear relationship (correlation), -1 in the case of a perfect decreasing (negative) linear relationship (anticorrelation)[27] and some value between -1 and 1 in all other cases, indicating the degree of linear dependence between the variables. As it approaches zero there is less of a relationship (closer to uncorrelated). The closer the coefficient is to either -1 or 1, the stronger the correlation

Secret Steganography Code for Embedding(SSCE) Table

	CO	5	s	<	co	5	co	<	co		CO	<	CO		CO	<	CO	<	s
10	1	1	96	2	59	3	78	4	1 04	5	1 30	g	166	7	1 91	8	906	g	931
20	2	1 1	27	12	53	13	79	1 4	1 05	15	131	16	157	17	1 87	13	207	1 9	939
30	3	21	98	99	54	93	an	94	1 06	25	132	96	158	27	1 83	pft	908	99	233
40	Д	31	99	39	55	33	81	34	1 07	35	1 33	36	159	37	1 84	38	909	39	234
SO	5	41	30	42	.56	43	82	44	1 08	45	1 34	4Б	160	47	1 85	48	91 0	49	235
60	6	51	31	69	57	63	83	54	1 09	55	155	68	181	57	1 88	58	911	59	938
70	7	51	32	69	58	63	84	64	110	65	1 36	66	162	67	1 87	68	21 2	69	237
ЯП	g	71	33	72	54	73	as	74	111	75	137	76	1®3	77	1 88	79	91 a	79	рза
90	9	81	34	89	60	83	86	84	112	85	1 38	86	1 64	87	1 89	88	214	89	239
1 no	to	91	35	92	61	93	87	94	113	95	*1 39	98	185	97	1 40	49	91 5	44	940
110	11	101	36	109	62	1 03	88	104	114	1 05	1 40	106	166	107	1 91	1 OS	21 6	109	241
1 90	12	in	37	119	63	113	89	114	115	115	1 41	118	187	117	1 49	112	917	114	949
1 30	13	191	38	129	64	1 93	90	124	116	1 25	1 49	126	168	127	1 93	1 28	21 8	1 29	243
140	14	131	39	132	65	133	91	134	117	1 35	1 43	1 36	1 69	137	1 44	1 32	91 4	1 34	944
1 50	15	141	40	149	66	1 43	92	144	118	145	1 44	1 46	170	147	1 95	1 4R	920	1 49	245
1 АП	16	151	41	152	67	1 53	33	154	119	155	1 45	156	171	157	1 46	1 AR	991	159	24A
1 70	17	161	42	169	68	1 63	94	1 64	1 20	1 65	1 46	166	179	167	1 97	1 AR	922	169	247
1 Я0	18	171	43	179	69	1 73	95	174	1 21	175	147	176	173	177	1 98	1 78	223	179	24R
1 40	IS	181	44	189	70	1 80	98	1 84	199	1 85	1 48	188	174	187	1 49	1 8Й	994	1 84	944
200	90	191	45	199	у	1 93	57	1 94	1 23	1 95	1 49	196	175	197	200	1 9R	225	1 99	250
910	21	901	46	909	79	903	98	904	1 94	906	1 SO	908	178	907	901	902	998	909	751
920	92	211	47	91 9	73	21 3	99	21 4	1 25	215	151	21 6	177	217	202	918	227	21 9	262
900	93	991	42	999	74	993	103	994	1 96	996	1 59	998	179	997	903	992	992	999	753
940	94	231	49	939	75	233	101	234	1 27	235	1 53	236	179	237	204	238	229	239	254
950	25	941	50	949	76	943	109	944	1 98	945	1 54	948	190	947	90S	942	930	944	p55
		251	51	252	77	253	103	254	129	255	155

Figure 19: SSCE Table between the variables. If the variables are independent, Pearson’s correlation coefficient is 0, but the converse is not true because the correlation coefficient detects only linear dependencies between two variables.

If we have a series of n measurements of X and Y written as x i and y i where i = 1, 2, . . . n then the sample correlation coefficient can be used in Pearson correlation r between X and Y . The sample correlation coefficient is

IL ( x i - x ⁾⁽ y i - y )

written r = i =1.....................   ......... (6)

• ^ХУ       ( П - 1) ^ x ^ y

where x and y are the sample means of x and y , s x and S y are the sample standard deviations of X and Y. The number of matching (but different sequence order) characters divided by two defines the number of transpositions. The Correlation score of comparing cover text and stego text is shown in Fig. 11 and the chart in Fig. 12 represent the Correlation of different stego of various length of message.

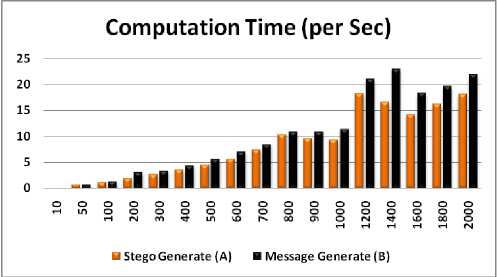
In Fig. 13 and Fig. 14 it has been observed that the cover and stego graphs both are remain same. The Fig. 15 and Fig. 16 shows that the Input and Output messages graphs are same; from this view also we can proof our technique. The computation time of Stego and Message generation exposed in Fig. 17 and the graph showing in Fig. 18. To observe the computation time it is proved that the receiver side message generation system is faster than sender side stego generation system.

• VI. C onclusions

In this paper the authors presented an approach of text steganography method using Gujarati language by the help of quantum truth table mapping technique. This property generates the stego text with minimum degradation. In this method the length of stego and cover remain same and this property enables the method to avoid the steganalysis also. The result shows that the performance of the technique is satisfactorily. Here the authors incorporate a Revised SSCE value which is depending upon the user’s entered Passkey to extend the security level. This work can be extended by using other Indian regional language.