Texture Classification based on First Order Local Ternary Direction Patterns

Published Online February 2017 in MECS

Texture characteristics provide important information for classification and retrieval of images. The challenging issues of texture descriptors are how to deal efficiently with variations in illumination, scale, orientation, etc... The constraints are the dimensionality and computational complexity. Texture is a fundamental feature of the appearance of object surfaces and is extensively used in object surface recognition and description. Texture is considered as a “neighborhood property”. One of the important and crucial tasks of image, video processing and pattern recognition is texture classification and it consequently requires the analysis of patterns in local pixel neighborhoods. The major challenges of texture classification are how to extract texture features that are insensitive to illumination changes, noise and rotationinvariant. An extensive work is carried out and a broad range of texture classification methods are proposed based on statistical properties of texture. This begins with the co-occurrence matrix method [1], which is one of the pioneering and still the bench mark method for texture classification. Later, a number of texture classification methods that were rotation- invariant are introduced. The well-known rotational invariant texture classification methods are based on: a circular autoregressive model [2], Markov random fields [3]–[5] and filter bank responses [6]–[10]. Recently texture classification methods based on local features gained lot of recognition in the research community, due to their ability in capturing more discriminative information of textures in local patterns for their respective applications. It started by the revolutionary approach derived by Ojala et al.to derive texture features by quantizing the local pixel values of a neighborhood in to two values and named it as local binary patterns (LBPs) [11,12]. Later several authors [13–19] carried out abundant work and derived efficient methods to further extend the benefits of LBP in various applications. The Binary features [12, 13, 15, 20, 21, 22] gained reputation and recognition due to their efficient design, computational simplicity and good performance. The LBP based methods are utilized in various applications, such as face recognition [23, 24,25], texture classification [26], facial expression recognition [27], age classification [28,29], image retrieval [30, 31, 32, 33], etc...The dimensionality of these descriptors grows exponentially by increasing the window size and number of neighbors considered resulting in, both, storage and computation complexity. After studying in detail on the methods based on LBP, we found one of the disadvantages of these methods is they completely ignored in measuring the directional features of texture information. The present paper derived a novel approach by measuring first order directional pattern measures between two neighboring pixels (yi , yj) located at an angle αo and βo around the central pixel. Many variants of LBP are proposed in the literature to improve the efficiency in representing the texture features: a variant of LBP used magnitude also as a descriptor[14],other variant discarded the some patterns with few occurrences[15], many researchers combined LBP with GLCM features and also with textons [16,36,37,231,9114]. The present also derived GLCM and its features on the proposed first order derivative patterns to increase the texture classification rate. Some researchers improved the threshold mechanism of LBP [34] to sustain against noise. The other approaches used vector quantization [38, 39, 40] to reduce the dimensionality.

A good classification results are obtained by LBP and many of LBP-like methods on different representative texture databases, they still have limitations. Firstly, the LBP and the related methods use scalar quantization in deriving binary patterns for neighborhood pixels, which is coarse. Secondly, they ignore completely the local texture derivative information. This paper addresses the above problems of LBP based methods by deriving a more efficient method called First Order Local Derivative Variation Pattern (FO-LDVP), which evaluates the relationship between the two first order derivatives along horizontal and vertical directions and represented this using a ternary pattern for deriving a new and more comprehensive local descriptor. There will be four such relationships (0o Vs.90o; 90o Vs. 180o ; 180o Vs.270o ; 270o Vs. 0o) around a central pixel of a circular or rectangle neighborhood.

The rest of the paper is organized as follows. The LBP and LTP are briefly introduced with their limitations in section two. The section three gives a detailed description about the proposed method FO-LDVP while section four presents results and discussions. Finally the conclusions are drawn in section five.

• II.    Main Contribution

• A.    Local Binary Pattern (LBP)

LBP is a useful tool to model texture images and it is defined as a gray scale invariant texture measure. To invariance feature is achieved in LBP by deriving the gray level value difference from the central pixel and all other gray levels of the neighboring pixels. By using a sign function on this difference the local neighborhood is quantized in to binary pattern. This binary pattern is coded as 8-bit word on 3 x 3 neighborhoods with 8-neighboring pixels. This binary word is multiplied by binary weights and thus deriving to represent the 8-different-jont histograms as a 1-D histogram with 256 bins. This results a LBP code for each central pixel of a 3 x 3 neighborhood ranging from 0 to 255. This operation can be viewed as applying a bank of oriented difference filters [44]. The range of LBP codes grow large if the size of the neighborhood increases. The Fig.1 and Fig.2 show the formation of LBP code. The LBP code is evaluated by the Eq. (1) and (2).

Y 1	Y 2	Y 3
Y 8	Y C	Y 4
Y 7	Y 6	Y 5

Fig.1. A 3x3 neighborhood.

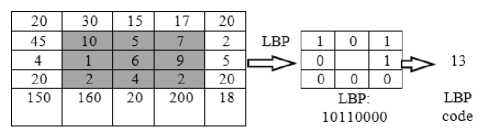
Fig.2. An example of calculating LBP code.

LBPp ,я= ∑Р=1 2 р-1 ∗/( Yp - Y_c )p=1,2…8        (1)

f ( Y ) = {^{1 Y}≥0 () = {₀ else

In Eq. (1), P is number of neighboring pixels, R is radius,Yp and Yc are the gray level value of neighboring and central pixel.

• B.    Local Ternary Pattern (LTP)

The concept of LBP is extended to three values code by Tan and Trigs [45] by adding a threshold factor t_f to the Y c. The pattern indicator f(Y) is quantized to zero, +1 and -1 based on Eq.(3)

LTPp , R = ∑p=l 3 P-1 ∗ f ( Yp - ^Yc )               (3)

+1 ^Yp ≥ Y_c + У

f ⁽ Y )= {0 | ^Yp ^- Y_c ^<  ^f |                   (4)

-1 Yp ≤ Y_c - tf

• C.    First Order-Local derivative variation Pattern (FO-LDVP)

The LBP and LTP are simple to implement, resistance to lighting changes and efficient ability to encode fine details. That’s why there are popular and widespread local descriptors among the researchers in computer vision and pattern recognition. The common problems of these (LBP and LTP based methods) are they all ignore the spatial distribution feature of texture in images e.g., the varying texture features in different directions. This will cause some loss of significant and useful texture information and by which the classification performance will be degraded. In conclusion, LBP and LTP derives the texture information based on grey level variation pattern of pixels, which is coded using only two directions (positive direction or negative direction) and they completely ignore the information regarding the direction of local features. This observation made us to propose the computation of gray-level derivative variation patterns on different directions and construct the spatial distribution pattern. The present paper evaluated the possible ternary directions for central pixel by measuring the first order derivates relationship among the horizontal and vertical neighbors (i.e. 0o Vs.90o; 90o Vs.180o; 180o Vs. 270o; 270o Vs. 360o). From this, the proposed FO-LDVP derived a number for the 3x3 neighborhood ranging from 0 to 80 and the detailed description is given below.

The present paper derived four first order derivatives along 0o, 90o, 180o and 270o around the central pixel of the neighborhood and they can be written as f^ ( Yc ) =f(14) -/( Yo )

Год" ⁽ Y_c ) = f ⁽ Y_г ) - f ⁽ Y_o )

/180° ( Y_c ) = f ( Y_B ) - f ( Y_o )

Ггод" ( c ) = f ( Y₆ ) - f ( Y_o )

The present paper derived local direction patterns in between the above two derivates of first order and named it as “First Order – Local derivative variation Pattern (FO-LDVP)”. The present paper derived four different First Order (FO) Local Derivative variation Patterns between two neighboring pixels located with angle of α^o and β^o around the central pixel. The four FO-local derivative patterns are defined as i.0^o Vs. 90^o ( D^ ₍ Y_c )) ii. 90^o Vs. 180^o ( Dk ₍ Y_c )) iii. 180^o Vs. 270^o ( D^ ₍ Y_c )) iv. 270^o Vs. 0^o ( D^ ₍ Y_c )).

The proposed FO-LDVP assigns a ternary pattern (0, 1, 2) by comparing the two neighboring pixel gray values (yi, yj) located at angle αo and βo respectively with the central pixel (two local derivatives). These ternary patterns represent the derivative direction patterns of the central pixel along with its two neighboring pixels (yi, yj).The  present paper transforms these derivative variation patterns into a decimal number to represent the direction of the structural pattern. This decimal number is denoted as FO-LDVP code. The present paper defined the possible direction of the central pixel in each of the above four first-order derivative directions with a ternary value (0, 1, 2) as given in the Eq. (5). The Eq. (6) gives the FO-LDVP code.

• 2    fa" ( Y_c ) ≥0 ciTtd. fpo ( Y_c ) ≥0

• ⎪ 1 fa" ( Y_c )<0 and fpo ( Y_c )>0

D’_d ( Y_c )=                    or                   (5)

fa" ( Y_c )>0 and fpo ( Y_c )<0

• ⎩ ⁰    fa" ( Y_c )<0 and У^ 0 ( Y_c )<0

FO - LDVP = ∑ D = 1 3 D-l ∗ ^Dd ( Y_c )           (6)

for d={1,2,3,4}

The Eq. (5) gives three possible derivative direction values for central pixel in each case. This derives four ternary pattern values on a 3x3 local neighborhood and by multiplying them with ternary weights and later concatenating them, will yield FO-LDVP code as given in Eq. (6). The FO-LDVP code ranges from 0 to 80. The Fig.3 illustrates FO-LDVP around the central pixel Yc considered in this paper.

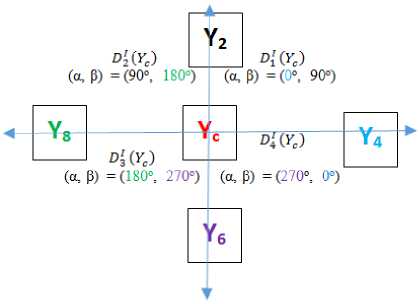
Fig.3. Representation of four FO-LDVP.

The central pixel Y c is marked with red color. The pixel that forms an angle 0^o, 90^o, 180^o and 270^o are shown with blue (Y 4 ), black (Y 2 ), green (Y 8 ) and purple (Y 6 ) colors respectively.

An example of FO-LDVP along the four different directions with respect to central pixel is given in Fig.4. When we apply the Eq. (6) for first combination i.e. α= 0o and β= 90o (Y2<-Yc->Y4), it has resulted a ternary value 2. In the same way the other combinations α=90o and β=180o (Y8<- Yc->Y2) resulted a ternary value 1 and other two ternary values for the combinations α= 180o and β= 270oand α= 270o and β= 0oare computed and shown in Fig.4. This results a FO-LDVP code 32 for the

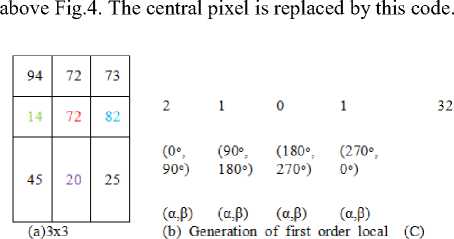
neighborhood ternary directional pattern (FO- FO_LTDijP LTDifP)                           code

Fig.4. Generation of first order local derivative variation pattern (FO-LDVP ) code.

• D. Gray Level Co-occurrence Matrix (GLCM)

• 7.    Entropy:

The present paper derived GLCM and other features on the FO-LDVP matrix image for efficient classification. The grey level range of FO-LDVP matrix ranges from 0 to 80. Therefore the size of the GLCM on FO-LDVP will be 81 x 81. The GLCM is one of the popular and bench mark method and it was derived by Haralick et al. [1]. GLCM is a second order statistical method. Construction of GLCM is based on the spatial relationship between gray tones in an image [46] and with this property it is able to characterize texture images very efficiently. The GLCM computation is given below: Initially the original texture image I quantized with reduced number of gray levels, from 0 to g-1. Then, GLCM is computed from the quantized image by scanning the intensity of each pixel and its neighbor, defined by displacement d and angle ø. A displacement, d could take a value of 1, 2, 3…n whereas an angle, 0is limited 0°, 45°, 90° and 135°. The following Fig.5 illustrates the formation of GLCM with different angles (0°, 45°, 90° and 135°) from a given window.

3	3	3
1	3	3
1	3	2

0o	1	2	3
1	0	0	2
2	0	0	0
3	0	1	3

=  ∑   ∑     ( , )-   (12)

Entropy= -∑   ∑     ( , )∗log( ( , ))    (13)

• 8.    Root mean square (RMS)

  45o	1	2	3
  1	0	0	2
  2	0	0	0
  3	0	0	2

  
  

  135o	1	2	3
  1	0	0	0
  2	0	0	1
  3	0	0	2

  
  

  90o	1	2	3
  1	1	0	1
  2	0	0	1
  3	0	0	3

  
  
  
  

  RMS= √ (  +   +  +⋯․+  )    (14)

  
  

  Skewness : The skewness of a distribution is defined as

  
  

  (      )

  =

  
  
  
  

  Fig.5. An example of GLCM formation. (a): The sample window. (b) (c) (d) and (e ) are 0^o, 45^o,90^o and 135^o degrees GLCM matrix of (a) respectively with a distance d=1;

  The present paper initially constructed GLCM on FO-LDVP with d= 1, 2, 3 and 4 and with 0^o, 45^o, 90^o and 135^o degrees. The four GLCM features i) Contrast, ii) Correlation, iii) Energy iv) homogeneity with 0 ° , 45 ° , 90 ° and 135 ° are evaluated on the referred database images and average of these are considered for texture classification. The four GLCM features are given below:

  1. Contrast :

  Contrast = ∑      {∑   ∑     ( , )},| - |=   (7)

  
  
  
  

  Variance

  
  

  ∑(    )

  =

  N

  
  
  
  

  11. Inverse Difference Moment (IDM): It is the local homogeneity. It is high when local gray level is uniform and inverse GLCM is high.

  
  

  =

  
  

  _VM-1_VN-1 y..

  ∑   ∑

  
  

  (     )

  
  
  
  

  Where X is image with size MxN

  
  

  12. Smoothness

  
  

• 2.    Correlation :

• 3.    Energy :

• 13.    Kurtosis: The kurtosis of a distribution is defined as

  4. Homogeniety, Angular Second Moment (ASM):

  
  

  (      )

  
  
  
  

Correlation = ∑    ∑    {  }  ( , ) {      }(8)

1Ox^Oy

ℎ    =1-(18)

∑     ∑( , )

where X is image

Energy:∑ ,    ( , )                 (9)

ASM= ∑   ∑   { ( , )}        (10)

Further the present paper evaluated the following nine features on GLCM of FO-LDVP image matrix: mean, standard deviation, entropy, root mean square error (RMS), variance, smoothness, kurtosis, skewness and inverse difference movement (IDM) with different orientations (0 ° , 45 ° , 90 ° and 135 ° ) and average of this is considered for classification. They are given below.

• 5.    Mean

• 6.    Standard deviation

=  ∑    ∑     ( , )                 (11)

The machine learning classifiers are used for classification purpose. Classification is done in two different ways one is only by considering the four GLCM features on FO-LTDP and the other is by integrating GLCM features on FO-LTDP with the other nine futures.

• III.    Experimental Results

To examine the efficacy of the proposed method, we carried out a series of experiments on two representative texture databases: Brodatz [47] and MIT VisTex [48]. The advantage of these different texture databases, they are constructed under different viewpoints, conditions of illumination, and scale. The present paper classified the textures in two ways with different displacements on various machine learning classifiers i) by using the only four texture features of Haralick ii) by integrating all the 13 features that are derived on the proposed GLCM on FO-LDVP as given in section C. The present paper measured texture classification rate using the following machine learning classifiers 1)Multi perceptron, 2) Naïvebayes, 3)J48 and 4) lbk. The proposed GLCM on FO-LTDP is compared with other representative LBP schemes, such as the LBP[12], the LTP [45], the CDTM scheme [49]] and TS [50] approaches.

A. Experimental Results on Brodatz Database

We selected 10 homogeneous texture image classes from the Brodatz database, as shown in Fig. 6 (Granite, Bark, Wood, Marble, Stone, Gravel, Wall, Brick, Pigskin and Grass). In each class, we have considered 6 texture images. The texture images are of size 512 x 512 pixels. Then, each image is divided in to 64, non-overlapped patches of size 64 x 64. In this way, we generated a dataset containing 3840(10 x 6 x 64) texture images, and with each class or category containing384 images. We have considered 3-texture images (3 x 64 = 192) in each category as training and other remaining three images (192 sub images) as test images, i.e. 50 % of images in each class are considered as test images. Test images are not part of database images.

Out of this 50 % of images are considered for training data set in each class.

Fig.6. Brodtaz texture database.

The table 1 and 2 shows the average classification rate by the proposed FO-LDVP method with four GLCM features and integrated features (13 features) respectively, with varying distances by using machine learning classifiers on both considered data bases. The graphs of Fig. 8 and Fig. 9 shows the classification rate of the proposed method. The graphs clearly indicates the proposed integrated GLCM features of FO-LDVP have shown high classification rate for d=3 and by using Ibk classifier. The Fig.10 compares the performance of the proposed FO-LDVP method for d=3 using 4-GLCM and integrated features and integrated features on proposed method shown high classification rate on all classifiers.

Table 1. Average classification rate of the proposed FO-LDVP using GLCM features.

Texture database	Classifiers	Classification rate (%)
		Distance value d on GLCM
		d=1	d=2	d=3	d=4
Brodtaz	Multilayer Perceptron	83.69	84.58	85.04	84.48
	Ibk	84.74	88.45	90.47	89.78
	J48	85.36	87.36	89.69	87.82
	Logistic	74.85	78.68	79.35	77.85
MIT VisTex	Multilayer Perceptron	80.49	81.42	82.48	82.01
	Ibk	83.14	85.41	87.48	86.48
	J48	79.89	80.76	82.75	81.45
	Logistic	69.48	70.88	75.74	74.87

B. Experimental Results on MIT VisTex Database

The MIT VisTex database is an alternative collection for Brodatz texture library and images of this are representative of real world conditions. These images do not conform to rigid frontal plane perspectives and studio lighting conditions. The MIT VisTex also comprises examples of many non-traditional textures. The present paper used 10 classes of MIT VisTex album texture images with 128×128 pixels and in each class 6 images are selected randomly. The classes of MIT VisTex images considered are (Bark, Brick, Grass, Wall, Stone, Gravel, Water, Granite, Wood and Marble) and shown in Fig. 7. Each texture image is sub divided in to sub images of size 64 x 64. This results a total of 4 sub images for each image and a total of 240 (10x 6x 4) image databases.

Table 2. Average classification rate of the proposed FO-LTD ir P using all 13 features.

Texture database	Classifiers	Classification rate (%)
		Distance value d on GLCM
		d=1	d=2	d=3	d=4
Brodtaz	Multilayer Perceptron	92.15	95.13	97.22	96.45
	Ibk	93.25	96.49	98.48	96.68
	J48	89.78	91.45	94.91	93.89
	Logistic	94.15	96.59	97.37	95.78
MIT VisTex	Multilayer Perceptron	84.68	87.68	91.2	90.24
	Ibk	74.85	80.41	89.95	86.36
	J48	72.65	79.68	86.68	84.69
	Logistic	80.16	84.41	89.67	87.16

Classification rate

Brodtaz

VisTex

Databases and Classifiers

^^^^^еd=3(With only GLCM features)

^^^^^wd=3( With all 13 features)

Brodtaz

VisTex

Databases and Classifiers

• d1 ■ d2 * d3       d4

Fig.10. Classification graph for the proposed method with integrated features (all 13 features) and with four GLCM features for d=3.

The Table 3 and 4 shows the classification results over the Brodatz and VisiTex database of the proposed and other methods, which are based on LBP model.

Fig.

.8. Classification graph using four GLCM features for the proposed method using various classifiers for d= 1,2,3 and 4.

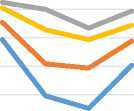
Table 3. Classification rate on Brodtaz database.

Methods	Classification rate (%)
LBP	40.58
LTP	57.85
LBP with variance	66.61
TS[50]	38.98
CDTM[49]	82.73
Proposed FO-LTDP with only 4 features of GLCM for d=3	91.62
Proposed FO-LTDP with integrated features (13 features as Specified in section C)d=3	98.69

Brodtaz

VisTex

Databases and classifiers

^^^^^еd1 ^^^^^w d2 ^^^^^w d3 ^^^^^^ d4

Fig.9. Classification graph for the proposed method with integrated features (all 13 features)

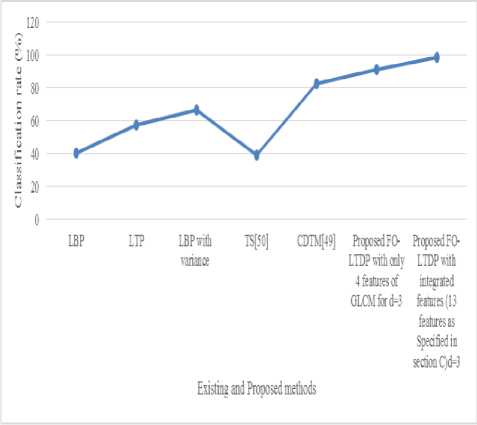
Fig.11. Comparison graph of proposed and existing methods on Brodtaz database.

Table 4. Classification rate on MIT VisTex database.

Methods	Classification rate (%)
LBP	39.95
LTP	52.36
LBP with variance	64.21
TS[50]	38.21
CDTM[49]	80.45
Proposed FO-LTD ir P with only 4 features of GLCM for d=3	89.68
Proposed FO-LTD ir P with integrated features (13 features as specified in section C) for d=3	92.74

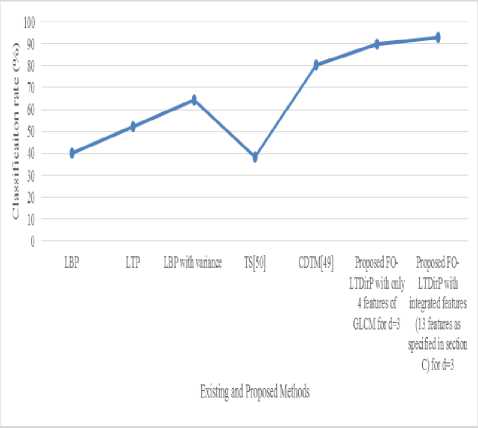
Fig.12. Comparison graph of proposed and existing methods on MIT VisTex database.

Table 3 shows the experimental results of all the listed methods. The LBPv achieves better results than LBP because it captures the magnitude information of the difference vector; however the coarse quantization over the variance limits its performances.

The results are presented in Table 3. As we can see from there, reducing the dimensionality of our feature vectors decreases the classification accuracy but the performance drop is relatively small. In particular, the achieved results still outperform those obtained for conventional LBP and LTP based approaches and show that we are able to derive an improved texture descriptor that is as compact and provides improved texture classification with reduced dimensionality. The best results are obtained for d=3 and on lbk classifier. Our experimental results, obtained from two representative databases (MIT Visitex and Brodatz), clearly show that FO-LDVP has higher texture classification accuracy than LBP and LBP-like methods.

• IV.    Conclusions

In this paper, we explored two disadvantages of LBP and LBP-like methods and found that they have ignored completely the direction responses around the central pixel. In this paper we have proposed a novel approach referred as FO-LDVP for texture image classification. The FO-LDVP used first order horizontal and vertical pixels relationship with central pixel and derived a ternary direction pattern. This process is continued for both horizontal pixels and vertical pixels around the central pixel i.e. 0o Vs. 90o, 90o Vs. 180o, 180o Vs. 270o and 270o Vs. 0o. The performance of the proposed method is compared with the LBP, LTP, LBPv, TS and CDTM methods. The range of FO-LDVP greatly reduced to 0 to 80 when compared to 0 to 255 (in case of LBP) and 0 to 3561 (in case of LTP). Finally, we derived the GLCM on FO-LDVP and this will have a dimension of 80 x 80 and it also reduced the dimensionality of GLCM from 255 x 255 and 3561 x 3561 in case of LBP and LTP based methods respectively. The extensive experiments results on the two referred data bases clearly demonstrate that the proposed approach outperforms LBP and LBP-like methods.