Texture Classification based on Local Features Using Dual Neighborhood Approach

Published Online September 2017 in MECS

Texture is one of the very fundamental and important appearances of the object surface. Texture is widely used in object surface recognition and description. Texture classification plays an important role in texture analysis. Classification and analysis of textures has wide range of applications, for example, in industrial inspections, medical image processing, face recognition, problems related to human faces like face, facial expression, age classification issues, remote sensing, etc. The texture classification method initially compares the features of a unknown test sample, with the training sample features with respect to spatial scale, orientation, grey scale properties etc... Then the unknown sample is given the class of training sample that is more identical or whose distance measure is least. Texture classification mainly dependent on the features extracted on the image or object surface. Numerous methods are derived in the past decades, to extract the features from local patterns in texture classification [1-5].

In the literature rotation invariant approaches has been developed. Circular auto regressive model are initially used to derive rotation-invariant texture classification [2]. Recently texton distribution methods are used for texture classification [3, 6, 7] and also for age classification [8].The revolutionary work of Ojala et al. “local binary pattern (LBP)” is extensively used for rotation invariant texture classification these days [9]. The LBP attracted increasing attention among the research scholars because of low computational complexity and invariance to monotonic illumination changes and rotation. The rotation invariant uniform LBP (LBPriu2), proposed by Ojala achieved a good rotational invariance performances. Later the original LBP operator [10] has been extended in several ways, such as neighborhoods with different sizes [9], multi-resolution [11], uniform patterns [12], prominent- LBP [31] etc. These developments on LBP mostly focus at capturing more discriminative and rotationally invariant information in local patterns and has a wide application, such as texture analysis and classification [13-16], face detection and recognition [17 - 25], image retrieval [26], etc.

The other variant of LBP called local ternary pattern (LTP) [27] quantized the difference between a pixel and its neighbors into three levels. Some variants of LBP, such as derivative-based LBP [28], dominant LBP [29] and center-symmetric LBP [30], prominent LBP [31], dual LBP [26] have been proposed recently to overcome the noise and other related problems of LBP. The PLBP [31] derived new transitions that contains set of ULBP’s and NULBP’s and achieved prominent results in face recognition. Another variant of LBP descriptors [32], combined LBP and co-occurrence features. In local quantized patterns (LQP) [33], a clustering method was adopted. The local color vector binary pattern (LCVBP) [34] is especially developed for color image applications. A texture classification method named local vector quantization pattern [LQVP] [35] developed recently aimed at quantizing the whole difference vector between the central pixel and its neighborhood pixels instead of each neighborhood pixels separately and it attained a good classification result on UIUC, Outex and Brodatz data bases.

Randen and Huso [36] after an extensive comparative study involving dozens of different spatial filtering methods concluded that the degree of computational complexity of most proposed texture measures in the literature is too high. To address this, the paper proposes a new feature description called ULBP-dual texture matrix (ULBP-DTM) for rotation and gray-scale invariant texture classification. At first, our approach quantizes the given texture image into ULBP coded image, this preserves the rotational invariant and fundamental units of texture image. The next step further quantizes the given ULBP texture image with ternary values and evaluates texture units by splitting the each 3 x 3 neighborhood in to dual neighborhood (cross and diagonal neighborhoods) of 4 pixels each. The GLCM features are evaluated on ULBP-DTM by using machinelearning classifiers for texture classification.

The rest of the paper is organized as follows. Section 2 briefly introduces LBP and its limitations; section 3 presents the derivation of ULBP-DTM. In Section 4 we present experimental results of proposed method and discussion. Finally, conclusions are drawn in Section 5.

• II.    Local Binary Patterns

LBP is a simple and efficient operator to describe local image pattern and it is a robust, theoretically and computationally simple approach. It brings together the separate statistical and structural approaches to texture analysis and this has resulted, a door for the analysis of both stochastic micro textures and deterministic macro textures simultaneously. The LBP has shown outstanding performance in many comparative studies, in terms of both discrimination performance and computational complexity. That’s why many researchers in the field of image and video processing are motivated to use LBP operator in their findings.

The derivation of the LBP follows that represented by Ojala et al. [9]. There is no universally accepted definition for texture. In general a texture T in a local neighborhood of a gray-scale image is defined as the joint distribution of the gray levels of P + 1 (P > 0) image pixels:

T = t(P c , P 0 , . . . , P n ),                     (1)

Where P c represents to the gray value of the center pixel and P n (n = 0, . . . , n-1) represent to the gray values of P equally spaced neighboring pixels on a circle of radius R (R > 0). That is according to LBP a texture is defined not only by the grey level values of a pixel P c also by the surrounding or neighboring pixels of P c . The neighboring pixel coordinates are given by (x_c + R*cos(2πp/P ), yc-R*sin(2πp/P )), where (x_c, y_c) are the coordinates of the center pixel. The values of neighbors that do not fall exactly on pixels are estimated by bilinear interpolation. Most of the textural information in an image can be obtained from local neighborhoods because correlation between pixels decreases with distance.

One can represent the local texture, based on the difference of grey level values between center pixel and neighboring pixels:

T = t(Pc, P0 - Pc, . . . , Pn - Pc) (2)

The above representation of texture is not true due to the limited nature of the values in digital images, further this representation describes the overall luminance of an image, which is unrelated to local image texture and does not provide useful information. The LBP measures only the signs of the differences, to achieve invariance with respect to any monotonic transformation of the grey scales. The LBP operator assigns a binomial weight 2^p to each sign S(P n - P c ).This transforms the sign differences in a neighborhood into a unique LBP code. The code characterizes the local image texture around (x_c, y_c). In practice, Eq. 4 represents the LBP code or local grayscale distribution which results in 2ⁿ distinct values. The process of formation of LBP code is shown in the Fig.1.

T~t(S(P 0 –P c ), . . . , S(P n-1 – P c )),            (3)

where

S(x) = 1 if x >= 0 else 0

LBP p.R (X c ,y c )=Z F= ^- o ¹5CP _/ - P_c)* 2^;

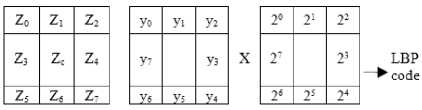
Fig.1. Representation of LBP.

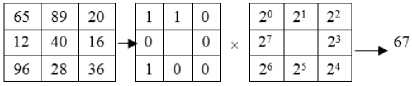
Fig.2. The derivation of basic LBP code.

A 3 x 3 neighborhood with 8-neighboring pixels derives a LBP code that ranges from 0 to 28-1= 0 to 255. The Fig.2 illustrates the process of LBP code derivation. The centre pixel 40 is replaced by the obtained LBP value 67. In this way a new LBP image is constructed by replacing the centre value with the corresponding LBP code. There is no unique way to label the coefficients and ordering the 255 LBP codes on a 3×3 neighborhood. The eight elements may be ordered differently. If the eight elements are ordered clock wise around the central pixel, the first element may take eight possible positions from top left corner to the left middle. This will result labeling of LBP code in 8-different ways. This will result 8-different LBP codes for the Fig.2 {13, 26, 52, 104, 208, 161, 67, 134}.

• III.    The Derivation of ULBP-DTM

  The number of LBP codes will be increased drastically if one increases the number of neighboring pixels (P) from 8 (2⁸ ) to 16 (2¹⁶) or 24(2²⁴) over a radius R. To quantify the varying performance of individual pattern attributes to the spatial structure of patterns the uniformity measure ‘U’ on LBP is defined. The uniformity corresponds to the number of circular spatial transitions (bitwise 0/1 changes) in the LBP. A LBP is treated as Uniform LBP (ULBP) if it contains at most two transitions from 0 to 1 or 1 to 0 in a circular manner. The remaining patterns are treated as non–uniform LBP (NULBP). The Pattern with 00000000, 01000000 and 01010101, derives 0, 2 and 8 transitions respectively. A LBP with (P, R) where P=8 and R=1 will have P * (P-1) + 2 = 58 ULBPs and 198 NULBP’s. Some of the researchers [37, 38] considered only ULBP’s because of the following reasons. a) The fundamental properties of texture image can be precisely represented by ULBP. b) 90 to 95% of the texture images hold only ULBP windows. c) Treating the 192 NULBP’s as miscellaneous will reduce lot of dimensionality without losing the texture content. The present paper given unique code for each ULBP i.e. from 1 to 58 and the code 0 is assigned to all remaining 198 NULBP’s. The quantization process of the basic 3 x 3 neighborhood in to ULBP coded image is shown in Fig.3. Here the central pixel 75 is replaced with zero (NULBP code) because the LBP window is a NULBP.

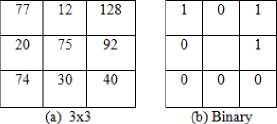
neighborhood             pattern.

Fig.3. ULBP quantization process.

(c)ULBP quantization.

The proposed ULBP-DTM initially quantizes the given grey level image in to ULBP window, by treating all noisy and non significant windows i.e. NULBPs in to miscellaneous. This quantization process represents the significant information of texture in the form of lines, curves, spots, blobs, edges etc… In the second step this paper further quantizes the ULBP coded image in to ternary representation by assigning one of three possible values (ternary patterns; 0, 1, and 2) to the neighboring pixels of ULBP windows i.e. using a threshold i.e. the grey level value of center pixel as specified in the equation 5.

(          0 if P i

c

T = ] 1 if P_t == P c   for i = 0,1,2, ... 7    (5)

I          2 if P i >P c

TUn =

and

ZT i *

i=0

3ⁱ ,T i e {0,1,2}

TU n e {0,1,2,^3^8-1}               (6)

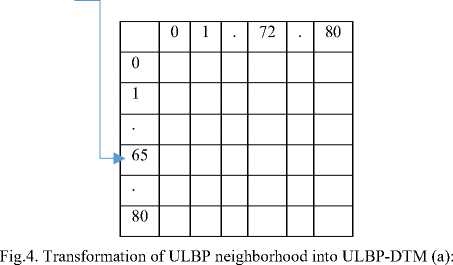
By assigning ternary weights to the ULBP neighborhood it generates a unique code ranging from 0 to 6561 as given in equation 6. The above ternary pattern approach on ULBP overcomes the sensitive to noise problem of LBP, which is particularly in the presence of smooth and weak illumination gradients in near uniform regions. That is ternary representation can better tolerate noise and it is significantly more distinctive. However one of the main disadvantages of this approach is it results a large set of TUn (0 to 6561) when compared to LBP (0 to 255) on a 3x3 neighborhood. To reduce dimensionality, while preserving the significant information this paper divided the ULBP ternary neighbourhood in to dual neighbourhoods and named them as cross-ULBP (CULBP) and diagonal-ULBP (DULBP). The CULBP and DULBP of a 3 x 3 neighbourhood consist of four pixels (Fig. 4). Multiplying each of the four ternary pattern elements of the CULBP and DULBP with ternary weights and concatenating them will result a code that ranges from 0 to 81 (34) as given in Eqn. 7 and 8. The CULBP and DULBP on a 3×3 grid can be represented in four ways as shown in Fig.5.1 and Fig.5.2 and this allows the formation of ULBP-DTM in 16 different ways. The ULBP-DTM is formed by placing CULBP code on the x-axis and DULBP code on the y-axis as in Fig.4. This ULBP-DTM has elements of relative frequencies of both basic windows and has a fixed size of 81 x 81. Since the values of CULBPn and DULBPn range from 0 to 80, the ULBP-DTM will have a fixed size of 81 x 81. This reduction is useful to reduce computational complexity of a GLCM. The GLCM method [40] gives reasonable texture information of an image that can be obtained from two pixels. The GLCM method characterizes the spatial relationship between a pixel and a neighboring pixel at a given specific distance and angle. The size of GLCM depends on gray level range of the image. The entire process of transforming an ULBP image neighborhood into ULBP-DTM is shown in Fig.4.

"■  ■    V/  Т,3 '-              (7)

N _DT u = ^ t=i T_t.3^i-1              (8)

12	5	2
53	10	8
14	15	10

a) 3x3 neighborhood with ULBP

2	0	0
2		0
2	2	1

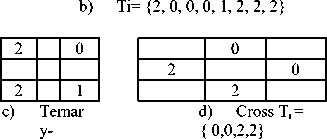
DULB P

30		31
33		32

Ternary weights for DTU DTU n = 65

	30
3 3		3 1
	32

e) Ternary weights for CTU

CTU n = 72

Ternary elements of DULBP and CULBP window; e & f) The ternary weights of DULBP and CULBP ( CULBP n & DULBP n ).

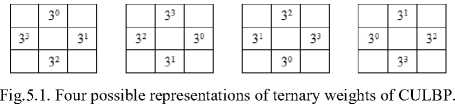
Fig.5.2. Four possible representations of weights of DULBP.

This paper evaluated 13 GLCM features on the ULBP-DTM using 0o, 45o, 90o and 135o degrees and performed the classification by computing average of these four rotations. The proposed ULBP-DTM model using GLCM combines the merits of both statistical and structural information of images and thus represents complete information of the facial image.

• IV.    Results and Discussions

This paper conducted experiments on three very large scale natural texture databases i.e. Brodtaz [41], UIUC [42] and Outex [43] and the experimental results are compared with other state of art methods CDTM [44], GLCM[40] , TS [39], TCTF [7]. The texture images of these databases are natural and captured under varying conditions like illumination, rotation, lightening, reflections etc…The present paper conducted experiments using various machine learning classifiers like Naïvebayes, Multi perceptron, Ibk and J48. This paper listed out the average classification rate, mean absolute error and root mean square error rates.

We selected 24 homogeneous texture image classes from the Brodatz database (Fig. 6). In each class, we considered 10 texture images. The texture images are of size 512 x 512 pixels. We extracted randomly 8 nonoverlapping patches with 128×128 size from each image. In this way, we generated a dataset containing 1920 (24 x 10 x 8) texture images, and with each class or category containing 80 images. We have randomly picked 20 texture patch images from each category as training and remaining are used for test images, i.e. 25% of images are considered for training purpose.

Fig.6. Sample image of Brodtaz textures.

The UIUC texture database is represented with 25 different categories of images, with 640×480 resolution, shown in Fig.7. The database contains images under significant viewpoint variations. This paper considered all 25 classes of UIUC database for experimental sake. And in each category we have randomly picked 10 images. We extracted 10 randomly non overlapped patches from each image with a size of 128 x 128. This makes the data base size of 2500 images with resolution of 128 x 128 (25 x 10 x 10). In each category we have used 20 texture patches as training set and remaining 80 images as test cases.

Fig.7. Sample images of the 25 classes from the UIUC database.

The Outex database includes two test suites: Outex_TC_10and Outex_TC_12 (TC12_000 and TC12_001) as shown in Fig. 8. Both TC10 and TC12 contain 24 classes of texture images captured under three illuminations (“inca”, “tl84” and“horizon”) and nine rotation angles (0° , 5° , 10° , 15° , 30°,45° , 60° , 75° and 90° ). There are twenty 128×128 images for each rotation angle under a given illumination condition. The 24×20 images of illumination “inca” and rotation angle 0°are adopted for the training process. For the TC10 dataset, we use the non-zero rotation angles with illumination “inca” for testing. For TC12 dataset, all the 24×20×9 samples captured under illumination “tl84” or “horizon” is used as the test data. In order to generate the codebook, we choose one image from each class on TC10 dataset, limiting the training set size to 24.

Fig.8. Sample images of the 24 classes from the Outex database.

This paper computed classification rates of textures on ULBP-DTM, using 13 GLCM features on the above three databases using NaiveBayes, Multilayer perceptron, Ibk and J48 classifiers on Weka tools . The 13 GLCM features in four principal directions are given as inputs to the classifiers and the average classification per texture class is listed in Table 1. We also computed average classification rate of each classifier on ULBP-DTM and presented in the last row of the table. The high classification rate is achieved by multilayer perceptron and in the remaining part of the paper, we will be mentioning this classification rate only on ULBP-DTM.

The paper evaluated the eight TS features [46] on all databases and average classification is listed in the Table 2. The eight TS features are 1) black-white symmetry (BWS), 2) geometric symmetry (GS), 3) degree of direction (DD), 4) micro-horizontal structures (MHS), 5) micro-vertical structures (MVS), 6) micro-first diagonal structures (MDS1), 7) micro-second diagonal structures (MDS2) and 8) central symmetry [46]. This paper also evaluated the 13 GLCM features on the raw texture image using 0o, 45o, 90o and 135o degrees and displayed the classification rate in Table 2. This paper evaluated the 13 GLCM features on CDTM [44] on 4-different ordering ways and the average classification rate is listed in the Table 2. This paper also computed the texture classification with our earlier method TCBTF [7] approach. The TCBTF [7] approach was only experimented on a particular type or category of textures i.e. stone textures of Brodtaz Texture, however in this paper we have tested the performance of this earlier method [7] on these three types of texture databases with huge number of images.

From Table 2 the following are noted down:

• •    The eight features derived on texture spectrum has resulted very poor classification rate of 55.36%.

• •    The TCTF and GLCM features have resulted a classification rate 80.44 and 61.29 respectively.

• •    The 13 GLCM features on CDTM with average of 4-different orientations has resulted good classification rate of 83.62.

• •    The proposed ULBP-DTM with the 13 GLCM features outperformed the other existing methods. The proposed ULBP-DTM achieved on average of 90.05% of classification rate.

• •    Outex and Brodtaz textures have resulted slightly higher classification rate on all approaches when compared to UIUC database. This is because UIUC database contains lot of orientations and scale changes when compared to other two databases.

The proposed ULBP-DTM exhibited more robustness to monotonic illuminations and other changes in the texture images than other methods due to the following reasons:

• 1.    The ULBP’s are fundamental rotation-invariant properties of local image texture consist of powerful texture feature.

• 2.    The ternary patterns derived on ULBPS resisted to noise and have shown more discriminative power.

• 3.    The division of neighborhoods, into dual neighborhoods reduced dimensionality to a greater extent, and that’s why the computational burden of evaluating GLCM features on ULBP-DTM is reduced to a greater extent from 256 x 256 to 81 x 81.

• 4.    The GLCM features derived on ULBP-DTM have shown high discriminative power on all databases.

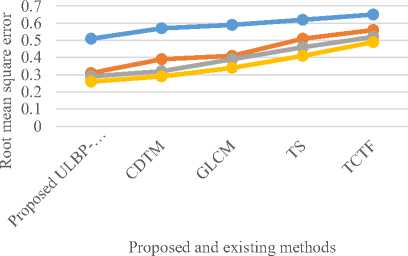
The graphs of Fig. 10, 11 and 12 , displays the average classification rate, mean absolute error rate and root mean squared error respectively on four different methods. The proposed ULBP-CDTM is resulted a high classification rate and low error rate on all databases when compared to the other existing method. The proposed ULBP-DTM method achieved on average classification rate of 90.05%, a low average mean absolute error of 0.30 and root mean squared error rate of 0.34 using multilayer perceptron classifier.

Table 1. Classification rate of proposed ULBP- DTM method on different databases using classifiers.

Databases/Classifiers	NavieBayes	Multilayer perceptron	Ibk	J48
Brodtaz	82.13	86.48	84.78	85.69
Outex_T10	91.98	95.41	88.15	88.45
Outex_T12	90.99	94.89	87.12	85.42
UIUC	81.78	83.43	81.15	81.78
Avg	86.72	90.05	85.30	85.33

Table 2. Classification rate of proposed and existing methods.

Databases/ Classifiers	Proposed ULBP-DTM method	CDTM	GLCM	TS	TCTF	Average classific ation rate per database
Brodtaz	86.48	82.46	60.18	54.76	79.56	72.68
Outex_T10	95.41	85.48	63.47	56.86	82.45	76.73
Outex_T12	94.89	87.86	64.82	57.63	84.44	77.92
UIUC	83.43	78.69	56.71	52.21	75.32	69.27
Avg	90.05	83.62	61.29	55.36	80.44

Classification rate (%)

я б 20

NavieBayes Multilayer     Ibk        J48

perceptron

Different classifiers

Brodtaz Outex_T10 Outex_T12 UIUC

Different databases

• Brodtaz     • Outex_T10

• •    Outex_T12 • UIUC

Fig.9. Classification rate of proposed ethod on considered databases.

• •  Proposed ULBP-DTM method

• • CDTM

• • GLCM

• TS

^*— TCTF

Fig.10. Comparison graph of proposed and existing methods on considered databases in terms of classification rate.

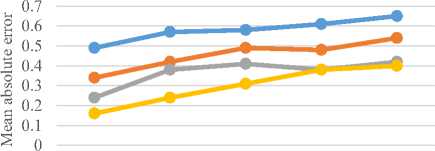
Fig.11. Comparison graph of proposed and existing methods on considered databases in terms of mean absolute error.

• Brodtaz     • Outex_T10

• Outex T12  • UIUC

Fig.12. Comparison graph of proposed and existing methods on considered databases in terms of root mean square error.

• V. Conclusions

  In this paper we integrated the structural and statistical features by deriving a new texture analysis method called ULBP-DTM and it is tested. The present method initially derived ULBP on the textural images to capture rotational invariant fundamental features and treated all 192 NULBP as miscellaneous. By this dimensionality is reduced while preserving the significant and fundamental features of textures. This paper derived ternary patterns on ULBP to reduce the effect of noise and to increase distinctiveness. To reduce the number texture units on ternary patterned texture the present paper divided the 3 x 3 neighborhood in to dual neighborhood and estimated texture units separately and established a relationship among them. This has reduced the dimensionality and derived a texture matrix of size 81 x 81 (in case of LBP it is 256 x 256 and 6561 x 6561 in case of TS). The performance of the proposed method has been compared with GLCM, TS, CDTM and TSTF. The performance of the proposed ULBP-DTM showed better performance

and proved to be an excellent gray-scale and rotation invariant texture descriptor.