The analytical dependence of the filling billets value to a given relative degree of deformation during cold rolling of tubes

For today to calculate the profiles of compression during rolling tubes used a hyperbolic dependence of the cross sectional area of tube (Fig. 1), in this case the degree of deformation of the billet is constant throughout the compression zone [1].

Determining the degree of deformation as e   = F (x) - F (x + 5)

F (x + 5)   ’ obtain the profile of compression zone (Fig. 1)

F ( x ) =

V ï

J e ( x ) dx + C

here F ( x ) - sectional area of tube at a point x in the compression zone [0, L],

V = F (0) m - volume of filling, m - linear filling rate, 5 - distance from the point x, at which fits volume of filling V_ï .

*

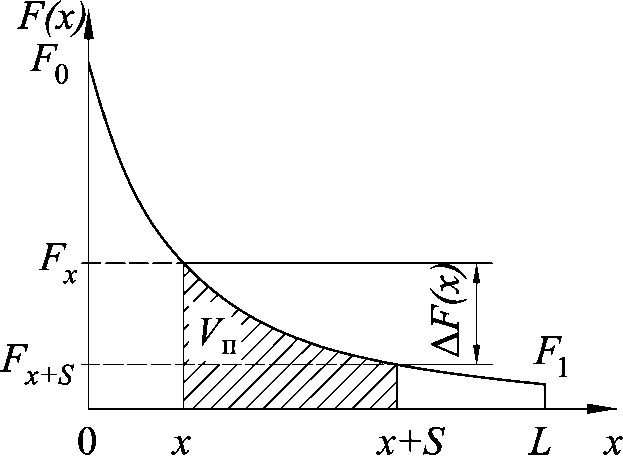
Fig. 1. Scheme of changes cross-sectional area of the tube along the deformation zone in cold rolling

At a given constant degree of deformation e ( x ) = e , integrating and using the initial conditions F 0 = F (0), F 1 = F ( L ), obtain:

F ( x ) =

F 0

X

(Ц f - 1) - + 1

F

Here: Ц _F = —

F ₁ obtain

- summary extract, F 1 - cross sectional area of the finished tube. Upon integration

F1 = Fm e L + m

.

From formula 3 the value of maximum filling expressed as m =

ε L

^ f ^- 1

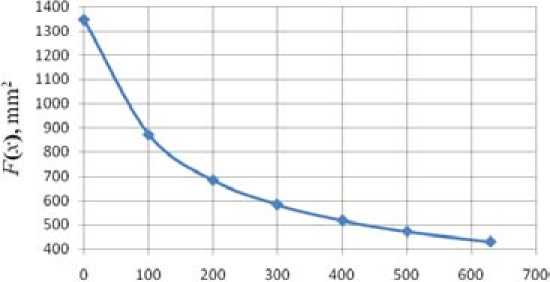
Consider the example of rolling tube diameter 77,5 mm, wall thickness 6 mm to 57 mm diameter tube with wall thickness of 2,5 mm. Fig. 2 shows a graph of change cross-sectional area of the tube on the hyperbola in the compression zone length of 633,35 mm. Filling equal to 12 mm, and the degree of relative deformation is constant and equal to 4 %.

It should be noted that, during rolling of aluminum alloy tubes private deformations limited by the plastic properties of metal, therefore, to maximize the productivity of the mills while maintaining high quality products it is necessary that along the length of compression zone change of the relative deformations decreased with a decrease in plasticity of the metal [1]. In this regard, it is the actual task of finding an analytic function to determine the maximum value of filling with a given degree of deformation.

Formula (2) is calculated with a given constant degree of deformation, which technologist selects averaged not to exceed the limit value. Therefore, we must choose a decreasing function of degree of deformation, such as a hyperbola

л; mm

Fig. 2. Graph of change cross sectional area of the tube along the deformation zone in cold rolling of tubes

е =----- a + bx

.

Using the given boundary conditions е(0) = е₀,е( L ) = е₁, where е₀ and е₁ - particular degree of deformation at the beginning and end of the compression zone, obtain

^{е (} x ) =-----Г°---- x

¹ + (^-1) x

N _ε    L

.

ε

Here N_е = ¹ - dimensionless quantity. By substituting the proposed degree of deformation in the ε₀

formula (1), after integration obtain [1]

F (x) =-----------------0----------r----- ln( N; + (1 - Nе ) x)

(Г F -1)(1--.-----^) + 1

Upon integration obtain

F =

F ₀ m

εεL ε

^{0 1} ln— + m

^е 0 ^{- е} 1

ε1

From here the value of filling is equal to m =

ε₀ε₁ L       _lnε _{0 .}

(е о -е , )(ц f -1) е , .

Denoting ε 0 , obtain г^е

ε1

0 ln µ

(Г е -1)(Г F - 1)

The quantity of feed (1.5) provides given starting and ending degree of deformation and decrease degree of deformation on hyperbola. In practice, can be taken ц_е = ц _F . If the filing determines the technologist, it follows from (1.5) obtain

= m (Ц f -1) 2

1   µFLlnµF and then e 0 = е1цF .

Thus defined initial and final relative degree of deformation for a given route, and filling. The technologist makes a decision on the application of the data, or changes the initial values. When considering the route of the rolling graph of changes in the cross section area of tube will look different (Fig. 3), in this case the relative degree of deformation varies from 7,6 % on hyperbole to 2,4 % (Fig. 4).

In conclusion, we consider another acceptable falling function of deformation degree – exponential e (x) = aeb.

Using the initial conditions, obtain the change of deformation degree

x e (x) = e о NL .

In this case, the sectional area of the tube varies according to the law

F ( x ) =

F 0

x

L

(Ц f —1) -^— + 1

N -1

and restrictions on filling would look like:

m = e о L ( N e - 1)

(Ц F -1)ln N e

1400 1300 1200

.. 1100 = 1000 4 900 3 800 ^ 700

600 SOO 400

0      100    200    300    400    500    600     700-

.V. mm

Fig. 3. Graph of change cross sectional area of the tube along the deformation zone in cold rolling of tubes

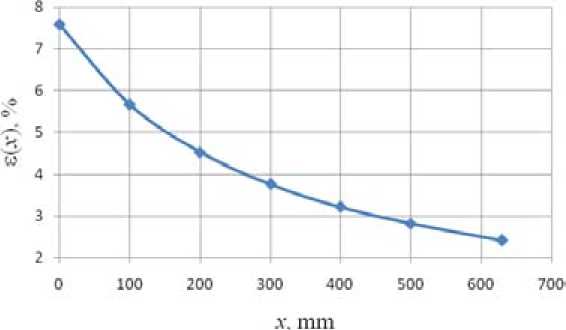
Fig. 4. Graph of change deformation degree of the tube along the zone of compression during cold rolling of tubes

In this case, you can also define the start and end deformation degree at a given by the technologist filing m mlnµ ε1 = L F и ε0=ε1µF .

Experimental tests at the Krasnoyarsk Metallurgical Plant on Long-mill CRT-100 showed, that the calculations of the stream caliber with a decreasing degree of deformation quality the tube especially critical applications is significantly improved, while rolling can be performed with the increase of 1.5 times the filling, rather than at a constant degree of deformation, which significantly affects the performance of the rolling mill.