The better pseudo-random number generator derived from the library function rand() in C/C++

Автор: Pushpam Kumar Sinha, Sonali Sinha

Журнал: International Journal of Mathematical Sciences and Computing @ijmsc

Статья в выпуске: 4 vol.5, 2019 года.

Бесплатный доступ

We choose a better pseudo-random number generator from a list of eight pseudo-random number generators derived from the library function rand() in C/C++, including rand(); i.e. a random number generator which is more random than all the others in the list. rand() is a repeatable pseudo-random number generator. It is called pseudo because it uses a specific formulae to generate random numbers, i.e. to speak the numbers generated are not truly random in strict literal sense. There are available several tests of randomness, some are easy to pass and others are difficult to pass. However we do not subject the eight set of pseudo random numbers we generate in this work to any known tests of randomness available in literature. We use statistical technique to compare these eight set of random numbers. The statistical technique used is correlation coefficient.

Еще

Pseudo-random number generator, library function, correlation coefficient

Короткий адрес: https://sciup.org/15017127

IDR: 15017127 | DOI: 10.5815/ijmsc.2019.04.02

Текст научной статьи The better pseudo-random number generator derived from the library function rand() in C/C++

The A sample program in C++ to generate 50 random members and print them is given below.

//A Sample Program to generate 50 random numbers

#include

#include using namespace std;

int main()

{ unsigned long int a[51];

int i;

for(i=1;i<=50;i++)

* Corresponding author.

E-mail address:

{

a[i]=rand();

cout<<" "<

if(i%10==0) cout<

} return 0;

} rand() is a library function contained in header file , it is a pseudo-random number generator (pRNG) which returns pseudo-random integer in the range 0 to 32767. It is repeatable, in the sense that every time above program is run the same sequence of random numbers are generated. One of the routines of rand() is illustrated below [1].

unsigned long int next = 1;

int rand(void)

{ next = next * 1103515245 + 12345;

return (unsigned int)(next/65536) % 32768;

}

Note that the random numbers are generated from a specific formula as given in routine, this mathematical formula is subject to change with time with attempts to generate better random numbers. Therefore this generator is called pseudo. However, because the numbers generated amongst themselves do not have any pattern they are called random numbers.

In this work we consider following 8 formulae of random number generators, all derived from the library function rand(), including rand() itself also as one of the formula.

In all of these formulae the effective power of rand() has been kept as one, but they generate different sequences of random numbers. So, a natural question that arises is, “Which is a better pseudo-random number generator amongst these eight ?” We answer this question in the sections to follow.

There are several other random number generators available in literature. In [2] following minimal standard random number generator has been proposed.

Ij+1 = a| (mod m)

a = 7s = 16807, m = 231 - 1 = 2 14748 3 6 47

[3] gives three random number generators ran0, ran1, ran2 based on the minimal standard discussed above. ran0 is a minimal standard. However, ran0 shows a low-order serial correlations. ran1 removes this defect of ran0 by shuffling its output. ran2 combines the generators ran0 and ran1 to give the best generator amongst ran0, ran1 and ran2. [4] chooses two different generators and combine them by either addition or subtraction to give a composite generator with very long periods, for eg., upto 2¹⁶⁰.
2. Correlation coefficient
2.1 Formula of correlation coefficient

However, in contrast, in our present work we do not take two different generators to find the composite generator but instead use the same generator rand() and combine them by multiplication and division. One advantage generating random numbers this way is that the range is increased, from 0 to infinity. We get infinity when value of rand() placed in denominator comes out to be 0. The largest integer generated in 1,00,000 iterations of pRNG given by formula 3 above is 4290421316, which is far more bigger than 32767 (the largest integer generated by rand() alone). Thus we have come up with pRNGs with a far more different and totally new recipe than the earlier works published in literature. The practical problem with pRNG generating infinity is that the computer does not understand it and the computer program will stop working after that. A remedy to this problem has been given in Result section to follow.

There are several tests of randomness available in literature. Some are easy as given in [5,6]. Marsaglia has worked exhaustively on these tests. Together with [7] he made up the Diehard Battery of Tests of Randomness which are included in a CD-ROM [8]. Tests more stringent than the Diehard Battery of Tests of Randomness: (1) The gcd Test, (2) The Gorilla Test and (3) The Birthday Spacings Test are given in [9]. These are a distillation of the Diehard Battery of tests.

These tests investigate absolute randomness amongst the members of data itself, i.e. they say whether a given sequence of unsigned integers is random or not. They, however, do not tell whether a given sequence is more random or not as compared to some other sequence. Hence in our present work we use the statistical technique of correlation coefficient to measure randomness in the sequence. This technique measures the relative strengths of randomness between different data sets. The data set with a lower value of correlation coefficient is more random than the data set with a higher value.

In C/C++ there is another library function srand(seed) to generate pseudo-random numbers [1]. With the use of this library function, every time we generate random number it is with a different seed, i.e. we can get different sequences of random numbers every time we run this routine. However, in this work we do not consider random numbers generated with srand(seed) library function. We will deal with this routine in future work.

Correlation coefficient, strictly speaking, is a measure of linear interdependence between two variables, say x and y of a data set [10]. We use it in our present work to measure the relative strength of randomness in multiple data sets. It is denoted by the letter r.

Consider the following data set

x	X1	X2	......	Xj	…..	x_n
y	Yi	y2	…….	y	…..	y_n

Let X = Xj — хц and Y= y, — y„ where хц and уц are respectively the means of variables x and y.

Then

X X Y r = ------ n Ox Oy where ox is standard deviation of variable x and ay is standard deviation of variable y.

Using the mathematical definition of standard deviation, the above equation for r can also be written as

X X Y r= , - -VX X2 X Y2

2.2 Interpretation of correlation coefficient

The value of r varies between -1 and 1. A high value of correlation coefficient shows strong correlation between the variables considered where as a low value shows weak correlation. Regardless of the sign the same numerical value of the positive correlation coefficient and the negative correlation coefficient shows a correlation of equal strength.

r=0 happens when the scatter of points (x j , y,), i = 1,2, ^.,n is totally random. r>0 happens when the line of best fit to the data set has positive slope. r<0 happens when the line of best fit to the data set has negative slope. As randomness in the scatter of points of the data set about the line of best fit reduces correlation coefficient moves away from 0. Thus correlation coefficient gives an idea of the relative strength of randomness between different data sets.
3. Result
- 3.1 Result based on Formula 1 to Formula 8 as stated above in section 1

In our present work we generate respectively 50, 100, 200, 300 and 400 random numbers by eight different formulae proposed in section 1 and find the correlation coefficient of each, for half of the data with respect to the other half, i.e. one half of the data is assumed the variable x and the other half is assumed the second variable y. Thus for the generation of 50 random numbers, sample size is 25 and we denote the absolute value of correlation coefficient for this sample size as r25. Thus for the sample sizes of 50, 100, 150 and 200 respectively the absolute values of correlation coefficients are denoted as r50, r100, r150 and r200.

A sample C++ program to generate 200 random numbers by Formula 3 given in section 1, and calculate correlation coefficient is given below.

//A Sample Program to calculate correlation coefficient

#include

#include using namespace std;

int main()

{ unsigned long int a[201];

int i;

unsigned long int x[101],y[101];

double sum1=0.0,sum2=0.0,sum3=0.0;

a[i]=pow(rand(),3)/pow(rand(),2);

cout<<" "<

if(i%10==0) cout<

} cout<

cout<<"Correlation coefficients";

sum1=sum1+double(x[j]);

sum2=sum2+double(y[j]);

{ sum1 = sum1+(double(x[j])-xavg)*(double(y[j])-yavg);

sum2 = sum2+pow((double(x[j])-xavg),2);

sum3 = sum3+pow((double(y[j])-yavg),2);

} r = fabs(sum1/sqrt(sum2*sum3));

cout<

N=25 N=50 N=100 N=150 N=200

Fig 1: The absolute value of correlation coefficients vs. sample size N for formula 1 to formula 8

Table 1: value of |r|ava for formula 1 to formula 8

Formula	\|Hav3
Formula 1	0.1028517
Formula 2	0.0423519
Formula 3	0.0232212
Formula 4	0.0411278
Formula 5	0.0165323
Formula 6	0.0255519
Formula 7	0.034642
Formula 8	0.0809405

We see from Table 1 that the absolute value of correlation coefficient is the lowest for formula 5, i.e. the linear interdependence between one half of random numbers generated and the other half is the least for formula 5.

3.2 Result based on new formulae of pRNG as stated below
One problem with pseudo-random number generators stated in formula 2 to formula 8 above in section 1 is that if the value of library function rand() placed in denominator in above formulae turns out to be zero, then the number generated is infinity and our computer program will stop to generate any further random numbers. We faced this problem with random number generator given by formula 2 above in section 1 in iteration number 8400. To overcome this problem we propose below following new formulae of pRNGs derived from the library function rand() of C/C++.

rand( )3 rand()*rand()+l

Formula 12:

rand( )4 rand( )3+l

Formula 13:

[rand( )*rand( )]2 rand( )3 + l

For these 7 formulae, i.e. formula 9 to formula 15, and formula 1 we generate respectively 50000, 100000 and 200000 random numbers and find the correlation coefficient of each, for half of the data with respect to the other half, i.e. one half of the data is assumed the variable x and the other half is assumed the second variable y. Thus for the generation of 50000 random numbers, sample size is 25000 and we denote the absolute value of correlation coefficient for this sample size as r. Thus for the sample sizes of 50000 and 100000 respectively the absolute values of correlation coefficients are denoted as ^ and r2.

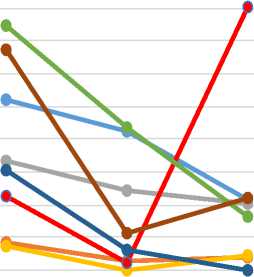
Same algorithm is used as given in section 3.1 but with different sizes of arrays a[ ], x[ ] and y[ ]. The plot of r, rl and r2 for different formulae is given below.

From Fig.2 we see that the curve for formula 11 is the closest to 0, on an average. This means that the absolute value of correlation coefficient is the smallest for formula 11, on an average, for all sample sizes and hence the randomness of the numbers generated by pRNG formula 11 is the greatest amongst the eight pRNG formulae compared.

However, from Fig.2 we can also find out mathematically the average of absolute value of correlation coefficient lrl_avg for each formula.

lrl_avg = Area under the curve for a chosen formula from Fig. 2/(100000-25000)

or Vrla^g = [0.5(r + ri)25000 + 0.5(ri + r2)50000] / 75000

The value of |r| _avg formula wise is given below.

0.009

0.008

0.007

0.006

0.005

0.004

0.003

0.002

0.001

N=25000 N=50000 N=100000

Formula 1 Formula 9 Formula 10

Formula 11 Formula 12 Formula 13

Formula 14 Formula 15

Fig 2: The absolute value of correlation coefficients vs. sample size N for formula 9 to formula 15 and formula 1

Table 2: value of lrla_V5 for formula 9 to formula 15 and formula 1

Formula	l^rlavy
Formula 1	0.00371158
Formula 9	0.00041733
Formula 10	0.00245084
Formula 11	0.00029679
Formula 12	0.00317576
Formula 13	0.0039695
Formula 14	0.00083501
Formula 15	0.00243022

We see from Table 2 that the absolute value of correlation coefficient is the lowest for formula 11, i.e. the linear interdependence between one half of random numbers generated and the other half is the least for formula 11.

4. Conclusion and Discussion

We can say from above result that the better pRNG (better than rand()) for short run, i.e. the number of iterations of random number generation algorithm around 400 is

rand()4 rand()3

But, however, the better pRNG (better than rand()) for long run, i.e. the number of iterations of random number generation algorithm equal to or in excess of 50000 is

rand()3

rand() *rand() + 1

This formula instead of rand() alone can be used in computer simulations, specially in Monte Carlo simulations. However, it is not applicable for cryptographic applications.

As stated earlier above, the pRNG formula 2 to formula 8 generates random numbers in the range 0 to infinity. Infinity as such is an undefined number, but if somehow we program our computer to manipulate infinity, these pRNGs are perfect random number generators and are better formulae than that given in formula 9 to formula 15. To find a way to make the computer manipulate infinity let us calculate the largest possible value that a given pRNG generates without rand() becoming zero. To be clear let us take the case of formula 3. The extreme possibility is that the value of rand() in numerator is 32767 and the value of rand() in denominator is 1. Now with these values consider the following algorithm unsigned long int a;

a=pow(32767,3)/1;

The problem with this algorithm is that it gives a warning- overflow in implicit constant conversion. And the value that is output to the terminal is 4294967295, which is not correct. A remedy to this problem is through following algorithm double a;

a=pow(32767,3)/1.0;

The output of this algorithm is 3.51812X1013, which is the correct value of mathematical operation carried out in the algorithm. So instead of creating integers if we create double precision floating point random numbers we immediately see a solution to infinity problem. For the particular case of formula 3 we modify our pRNG algorithm to create the random number “3.51812X1013 +rand()” whenever 0 is encountered for rand() in denominator. This way we have defined infinity for formula 3 to have value 3.51812X1013 + rand(). So if we create double precision floating point random numbers our pRNG formula 2 to formula 8 will turn out to be very-very good random number generators with exceptionally long periods.

Список литературы The better pseudo-random number generator derived from the library function rand() in C/C++

Kernighan, Brian W. and Ritchie, Dennis M., (1988), The C Programming Language, 2nd Ed., Pearson-Prentice Hall, New Delhi, India
Park, S.K. and Miller, K.W., (1988), Commun, ACM 31, 1192-1201
Press, W.H. and Teukolsky, S.A., (1992), Portable random number generators, Comput. Phys. 6, 521-524
Marsaglia, G. and Zaman, A., (1995), Some very-long-period portable random number generators, Computers in Physics, 8 117–121.
Knuth, Donald E., (1998), The Art of Computer Programming, Volume II, 3rdEd., Addison Wesley, Reading, Mass.
MacLaren, D. and Marsaglia, G., (1965), Uniform random number generators, Journ. Assoc. for Computing Machinery, 12, 83–89.
Marsaglia. G.,(1985), A current view of random number generators, Keynote Address, Statistics and Computer Science: XVI Symposium on the Interface, Atlanta, Proceedings, Elsevier.
The Marsaglia Random Number CDROM, with The Diehard Battery of Tests of Randomness, produced at Florida State University under a grant from The National Science Foundation, 1985. Access available at www.stat.fsu.edu/pub/diehard.
Marsaglia, G. and Tsang, W.W., (2002), Some difﬁcult-to-pass tests of randomness, Journal of Statistical Software, Vol 7, Issue 3.
Singpurwalla, D., (2015), A Handbook of Statistics: An Overview of Statistical Methods, bookboon.com (Ebook)

Еще

Статья научная