The calculation of the electrical conductivity of graphene nanofibers by discrete Fourier transformation method

Andrey Nomoev, Natalya Yumozhapova The calculation of the electrical conductivity graphene nanoribbons by discrete Fourier transformation method // Вестник Бурятского государственного университета. Химия. Физика. 2019. Вып. 2-3. С. 39-43.

Graphenenanoribbons (GNRs) are narrow strips of a one-atomic-layer thick twodimensional material made of carbon atoms arranged in a honeycomb structure. Its fascinating electrical, optical, and mechanical properties ignited enormous interdisciplinary interest from the physics, chemistry, and materials science fields [1, 2]. These nanomaterials boast potential solutions to downsizing of future electronics in both size and energy consumption, as well as opening the door to faster processing.

We have calculated the electronic properties of graphene within the density functional theory framework. We used the SIESTA code (Spanish Initiative for Electronic Simulation with Thousand of Atoms) [3], which employs linear combinations of numerical atomic orbitals to solve the Kohn-Sham equations with three dimensional periodic boundary conditions within a supercell [4]. This is convenient for treating infinite systems such as crystals, but can also handle finite systems by making the supercell sufficiently large separating the objects. The framework in the supercell approach is Bloch’s theorem, which states that for a periodic system the electronic wave function can be written as a product of a wavelike part and a cell-periodic part, i.e.

^(r') = elkX,kM where n is a discrete band index and k is a reciprocal lattice vector belonging to the first Brillouin zone corresponding to the supercell. The theorem allows for mapping the Kohn-Sham eigenvalue problem into the reciprocal space, where one can separately obtain for each k-point a discrete set of eigenvalues and eigen states of the Hamiltonian. The expectation value of some one-body operator ∂ is then calculated as

• (d) = — d4o(k)« ) Шко(к)

where for practical purposes the integral over the first Brillouin zone with volume Ω BZ is approximated by a sum over k-points with weight factors ω k (adding up to one). The numerical solution of the Kohn-Sham equation implies a finite basis set for the representation of the wave functions. The SIESTA method requires the use of atomic-like localized orbitals which guarantee the Hamiltonian and overlap matrix to be sparse. For each atom i positioned at R i a set of atom-centered orbitals is defined as a product of a spherical harmonic and a radial function

Xinlm^T^ Ф4п1 (Л)^!тп(Л)

where the distances are conveniently written in terms of ri = r — Ri and the angular momentum is labeled by l, m . The SIESTA basis implies that the calculation of the overlap matrix and most matrix elements of the Hamiltonian are two center integrals, which are effectively calculated within Fourier space where the convolution becomes a simple product. However, the density and some Hamiltonian matrix elements are calculated on a real-space grid, whose fineness is conveniently described by an energy grid cutoff. In SIESTA different parametrizations for the local density approximation and the generalized gradient approximation to the exchange-correlation functional are implemented. For our calculations we selected the generalized gradient approximation functional as described by the Perdew-Burke-Ernzerhof [5] which is proved to be one of the functionals that provide the smallest differences between calculated and experimental values in our field of interest. The current through the contact region has been calculated using Landauer-Buttiker formula [6]

K.Vb) = G0 T(E,Vb)dE

Where G 0 = 2(e²/h) is the unit of quantum conductance and T(E, V b ) is the transmission probability of electrons incident at an energy E through the device under the potential bias V b . The electrochemical potential difference between the left and right electrodes is eV b = µ L — µ R .

The calculation of the electrical conductivity using the TranSiesta package consists of the following steps:

• 1.    Obtaining for the equilibrium configuration of the simulated fragment.

• 2.    Generation of data on the construction and properties of electrodes (TSHS files), which contain the information necessary for calculating the electric current arising in the electrode — ribbon — electrode system at a finite potential difference.

• 3.    The calculation of the electrical conductivity, which begins with the usual procedure for calculating the density matrix using the Kohn–Shem scheme for periodic

systems. This calculation is used as input to the self-consistency procedure in the Green function method.

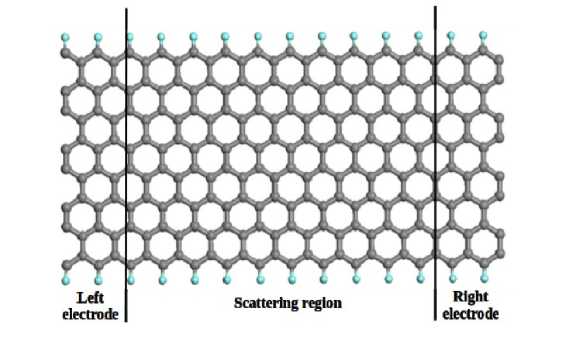
Fig. 1. Represented the response current for an electrode temperature of 300 K.

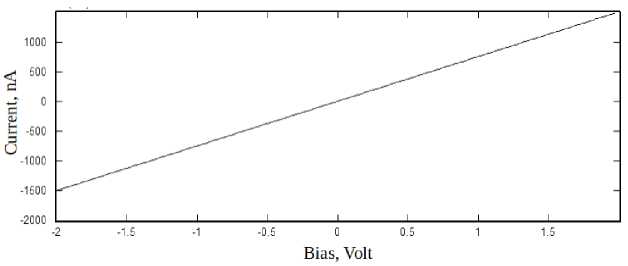
Fig. 2. Сurrent-voltage characteristics of the armchair GNR.

The figure below represented the response current for an electrode temperature of 300 K. The low-bias current-voltage (I-V) characteristic of the device are linear (fig. 2). Because the main contribution to the conductivity of GNRs is made by electrons. In a defectless armchair GNRs electrons pass through the nanoribbon without scattering, which corresponds to the quantum ballistic mechanism of conductivity.

Basic science has much to gain from studies of graphene. The electrical, optical, mechanical, and thermal properties of graphene achieve extreme values that are hardly met by any other materials. In this paper, we studied the electrical properties of graphenenanoribbon. We computed the current–voltage curve by method that come from the first principles methods.

This work was carried out according to the State assignment of the Institute of Physical Materials Science SB RAS and according to the RFBR project No. 18-42030004.