The Cayley graphs of finite two-generator burnside groups of exponent 7

Introduction. The definition of the Cayley graph was given by the famous English mathematician Arthur Cayley in the XIX century to represent algebraic group defined by a fixed set of generating elements.

During the last decades the Cayley graph theory has been developing as a separate big branch of the graph theory. The Cayley graphs are used both in mathematics and outside it. In particular, the Cayley graphs were used in information technology after the pioneering work of 1986 by S. Akers and B. Krishnamurti [1] who first proposed the use of these graphs to represent computer networks, including for topology modeling (i.e. methods of connecting processors to each other) multiprocessor computer systems (MCS) – supercomputersSince then, this direction is actively developing [2–11]. This is due to the fact that the Cayley graphs have many attractive properties, of which we distinguish their regularity, vertex transitivity, small diameter and degree with a sufficiently large number of vertices in the graph. Note that such basic network topologies as ”ring”, ”hypercube” and ”torus” are the Cayley graphs.

Let’s recall the definitions of the main terms used in the work.

Let X be a generating set of the group G , i. е. G = ( X ). The Cayley graph Г = Cay ( G , X ) = ( V , E ) is a named orgraph with the following properties:

• a)    a set of vertices V ( G ) correspond to the elements of G group,

• b)    a set of edges E (Г) consist of all ordered pairs ( g , xg ), where g e G и x e X .

Hence,

Г = Cay (G, X) = (V, E), where V = G andE = {(g, xg) |g e G, x e X} .

A number of vertices | V |is equal to the order of G . The Cayley graph is directed, and its degree s , i.е. the number of edges, going out of each vertice, is equal to the number of generating elements of the group: s = | X |.

We call the ball K s of radius s of a group G the set of all its elements, which can be presented as a group of words with length s in the alphabet X . For each nonnegative integer s , one can define the growth function of the group F ( s ), which is equal to the number of elements of the group G with respect to X , that can be represented as an irreducible group words with the length s . Thus,

F (0) = | K ₀| = 1, F ( s ) = | K s | - | K s — 1 |, s eN .

As a rule, the growth function of a finite group is represented in the form of a table which contains non-zero values of F ( s ).

Also, we note that, along with computing the growth function of a group, we define some characteristics of the corresponding Cayley graph, for instance, the diameter and the average diameter [12]. Let F ( s ₀) >  0, but F ( s ₀ + 1) = 0, then s ₀ will be the diameter of the Cayley graph of the group G in the generating alphabet X , which we will denote D_X ( G ). Accordingly, the average diameter D_X ( G ) is equal to the average length of minimal (irreducible) group words.

Unfortunately, although the computation of the growth function of a large finite group is solvable, it is a rather complicated problem. This is due to the fact that, in general, the task of the determination of the minimal word of a group element, as shown by S. Iven and O. Gol-dreich [13], is NP-hard (nondeterministic polynomial). Thus, in the worst case, the number of elementary operations that must be performed to solve this problem is an exponential function of |X|. Ih the case of large number of vertices in the Cayley graphs we need use MCS.

One of the widely used topologies of MCS is the k -dimensional hypercube. This graph is determined by the k -generated Burnside group of exponent 2. This group has a simple structure and is equal to the direct product of k copies of a cyclic group of order 2. Generalization of a hypercube is the n -dimensional torus which is generated by direct product of n cyclic subgroups wich may have different orders. In the articles [14–16] Cayley graphs of Burnside group of exponent 3, 4 and 5 are studied.

In this paper will research the Cayley graphs of some finite two-generated Burnside groups of exponent 7. We will use the algorithm from [16] to study the graphs. Since the orders of given groups are rather big we will apply MCS.

Cayley graphs study algorithm. Suppose B k = ( a 1 , a ₂ ^ is a finite two-generated Burnside groups of exponent 7 where a 1 and a 2 – generating elements and | B k | = 7 k . Using the computer algebra system GAP, it is easy to obtain pc-presentation (power commutator presentation) of this group [17]. In this case:

V g e B k ^ g = a x a x ² ... a x , x e Z ₇.

The basis for finding coefficients is a collection process (see [17, 18]) which is realized in computer algebra systems of GAP and MAGMA. Besides, there is an alternative method for product computation of group elements offered by F. Hall ([19]). Hall showed that z_i represents polynomial functions (in our case over the field Z ₇) depending on variables x 1 ,..., x i , y 1 , ..., y i which are now accepted to be called Hall's polynomials. According to [19]:

^z, = ^x, + y_t + P^{( x} 1 , . , ^x, - 1 , y 1 , . , y , - 1 ).

In the work [20] were calculated Hall’s polynomials of B k groups which allow to make product of group’s elements much quicker than via collection. On their basis we shall calculate the important special cases of polynomials necessary for further computation of Cayley graphs of B 14 groupand its factors.

• 1)    a 1 ■ a y a 2 ² ... a" = a y ^{+ 1} a y ² a ^⁴ ;

• 2)    a - ¹ ■ a y ¹ a y ² ... a 1 ^y 4 ⁴ = a y ¹ + 6 a y ² ... a 1 ^y 4 ⁴ ;

• 3)    a ₂ ■ a y ¹ a 2 ² ... a y = a Z a 2 ² ... a Z , where:

• ^z 1 = y^

z 2 = y 2 + 1,

• ^z 3 = y 1 ⁺ y 3 ,

• z 4 = ³ y 1 ⁺ у 4 ^{+ 4} y 2 ,

z 5 = У5 + У1У 2, z 6 = 5 У1 + У 6 + 3 У12 + 6 У13, z 7 = У 7 + 3 У1У 2 + 4 У12 У 2, z 8 = У 8 + 3 У1У 2 + 4 У1У 22, z 9 = 5 У1 + У 9 + 6 У12 + 5 У13 + 5 У14, zio = 2 У1 + У10 + 5 У1У 2 + 4 У1У з + 3 У12 У 2 + 3 У12 У з +

• ^{+ 6} У 13 У 2 ^{+ 4} У 12 ⁺ У 3 ,

zii = 5 У1 + У11 + 3 У1У 3 + 4 У12 У 3 + 3 У12 + 6 У13, z12 = У12 + 2 У12 У 2 + 6 У1У 2 + 5 У1У 22 + У12 У 2 + 6 У1У 2 У 3, z13 = У13 + 3 У1У 2 + 4 У12 У 2 + У1У 2 У3 , zi4 = У14+5 У1 у 2+ 3 У1 у 2+6 У1 у 2;

• 4)    a - ¹ ■ a ₁ ^{y i} а У ² ... a y = a z a z ² ... a z , where:

• z i    = У 1 ,

z 2 = y 2 + 6, z 3 = 6 У1 + У3, z 4 = 4 У1 + У4 + 3 У12, z 5 = У1 + У 5 + 6 У1У 2,

• ^z    6 = ² У 1 ⁺ У 6 ^{+ 4} У 12 ⁺ У 3 ,

• ^z    7 = ³ У 1 + У 7 + ⁴ У 1 У 2 ^{+ 3} У 12 У 2 ^{+ 4} У 12 ,

z 8 = 6 У1 + У 8 + 5 У1У 2 + 3 У1У 2, z 9 = 2 У1 + y 9 + У12 + 2 У13 + 2 y4, zio = 3 У1 + У10 + 2 У1У 2 + 3 У1У 3 + 4 У12 У 2 +

• ^{+    4 y} i2 ^y 3 ^{+ y} i3 ^y 2 ^{+ 3 y} i2 ^{+ y} i3 ,

z ii = ² y i ⁺ y ii ^{+ 4} y i У 3 ^{+ 3} У 1 У 3 ^{+ 5} У 3 ,

• ^z i 2 = y i ⁺ y i2 ^{+ 5} У 2 У 2 ^{+ 4} y i У 2 ^{+ 6} y i У 3 ⁺

• ^{+    2} y i У 2^{2 + 2} У 2 У 2 ⁺ y i У 2 У 3 ,

• ^z i 3 = ³ y i ⁺ y i3 ^{+ 4} y i У 2 ⁺ y i У 3 ^{+ 4} У 2 У 2 ^{+ 3} У 2 ^{+ 6} y i У 2 У 3 ,

• ^z i 4 = y i ⁺ y i4 ^{+ 4} y i У 2 ⁺ y i У 2 ⁺ y i У 2 .

Further the basic algorithm for computation of the Cayley graph of a finite group is provided [16].

Algorithm A–I

Input: a finite group     G = XX , °)    where

X = { x _i, x ₂,..., x m } is the generating set of G .

Output: the diameter D_X ( G ), the average diameter D_X ( G ) of the Cayley graph Г = Cay ( G , X ), and also growth function F ( s ) of the group G where 0 <  s <  D x ( G ):

• i.    s = 0, K o = { e }, F (0) = i, P = K o ;

• 2.    s = s + 1;

• 3.    K s = K s - i ;

• 4.    V x e X и V p e P :

  • 4.i.    g = x ° p ;

  • 4.2.    if g e K s , K = K и { g };

• 5.    P = K s - K s — i ;

• 6.    F ( s ) = | P |;

• 7.    if F ( s ) >  0, transition to 2; otherwise s ₀ = s - i, transition to 8;

• 8.    D x ( G ) = s 0 , D x ( G ) =      £ F ( s ) ■ s ;

• 9.    Exit.

| ^Ks 0I s = ⁰

In [16] is proved the correctness of algorithm A–I and also shown that T (| G |) e© (| G | ² ) under | X | « | G |, where T (| G |) is computational complexity of the algorithm A-I and © is simultaneously upper and lower complexity asymptotical estimate.

To lower the complexity a method for enumeration of elements is required. Suppose ax ...a^ k - random element from B_k . We shall define bijective mapping φ as follows:

Ф ⁽ g ) = ⁽ x k x k - i . x i ⁾ 7 ,

Ф ( ⁽ x k x k - i . ^x i ) 7 ) = al a x ² . a x = g .

Here ф ( g ) is an integer nonnegative number written in the sevenfold form, which we shall take as an ordinal number g . It is clear that ф ( g ) runs over values from 0 to (7 ^k - 1).

We modify A–I algorithm as follows. We shall add a Boolean vector of V of size 7 ^k to step 1, all elements of which originally are equal to 0. For convenience the indexing of elements of V begins with 0. As K ₀ = { e } and ф ( e ) = 0 therefore V ₀ = i.

Let’s replace the step 4.2 of the algorithm A–I as follows:

• 4.2.    ^{if V} ^ ( g ) = ⁰, K( g ) = ⁱ и K s = K s { g }.

As the complexity of the procedure of the group element transfer to a number and back is equal to © (i), according to [16] complexity of the modified algorithm A-I will be equal to © (| G |) .

Also, we shall note that in the step 4.1 all elements g are calculated independently of each other, therefore this section of the algorithm can be easily parallelized. In this case at first all products g are calculated simultaneously, then for every element do step 4.2 consequentially. Note that in step 4.1 products of group elements are calculated using Holl’s polynomials as suggested above.

The study of graphs B k . The modified algorithm A-I was implemented in C++. As a tool for parallelization, it was used the library OpenMP. For the calculations, it was used a computer with an 64-core processor and 512 Gb of RAM, running the Linux operating system. The program was compiled by the embedded compiler GCC. As the result characteristics of the Cayley graph of B k were calculated under k <  i4 for minimal ^ a ₁, aУ and symmetrical ^ a ₁, a _i ^{- i} , a ₂, a ₂^ generating sets. In the first case computation time under k = i4 takes about 18 hours, in the second – 36 hours. Table presents diameters D and average diameters D for the Cayley graphs of B k for the specified generating sets. For illustration in fig. 1, 2 growth functions of the group B 14 are presented.

Cayley graphs of group B _k characteristics

B k	B k = b, a 2)		B k = ^a-a a 1 ’, a 2 , a 2
k	D	D	D	D
2	12	6	6	3
3	14	8	8	5
4	18	11	11	7
5	23	15	12	8
6	28	17	15	10
7	28	20	17	12
8	35	23	21	14
9	36	26	22	16
10	39	28	24	18
11	42	31	26	20
12	43	34	27	21
13	49	37	31	23
14	56	41	34	25

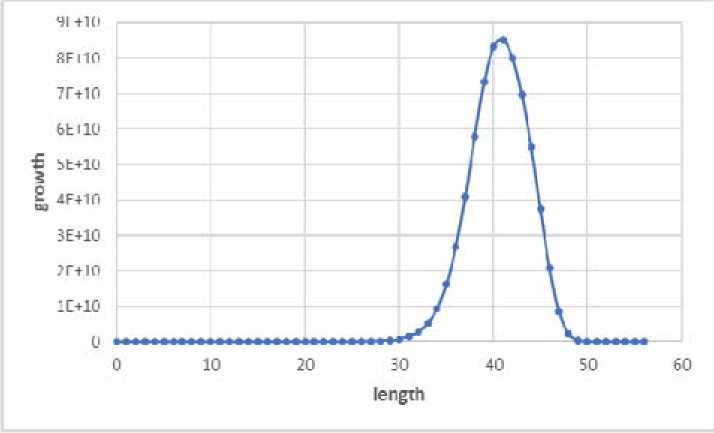
Fig. 1. The graph of the growth function of the group B ₁₄ = a a ,a a 2 ^

Рис. 1. График функции роста группы B₁₄ = ( a ₁ , a 2^

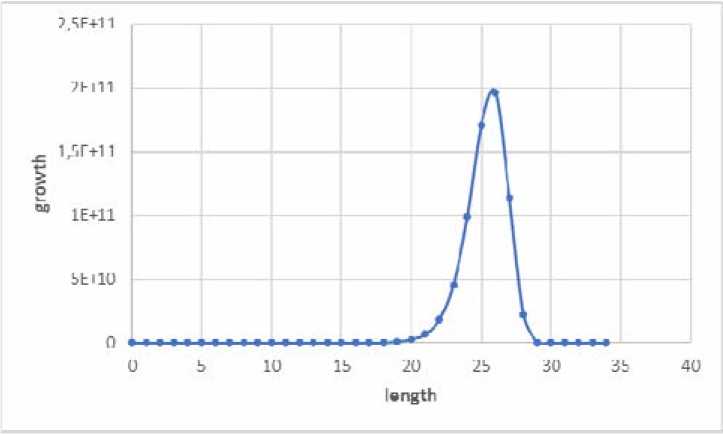
Fig. 2. The graph of the growth function of the group B ₁₄ = ( a 1 , a 1 1 , a 2 , a 2¹

Рис. 2. График функции роста группы B ₁₄ = / a 1 , a 1 1 , a ₂ , a ₂ ¹

Conclusion. As mentioned above the Cayley graphs represent an effective model for the topology of multiprocessor computing systems design. Therefore, for the creation of supercomputers with exaFLOPS performance (10¹⁸ floating point operations per second) knowledge of characteristics of super-large-scale Cayley graphs might be required. The results of this research can be used for perspective topologies design of MCS.

Acknowledgments. The reported study was funded by Russian Foundation for Basic Research, Government of Krasnoyarsk Territory, Krasnoyarsk Region Science and Technology Support Fund to the research project № 17-47-240318.