The choice of method of computer simulation for formation of pictures of danger of electromagnetic environment

The electromagnetic pollution of the environment is rapidly increasing, which justifies the need for monitoring and visualization of the electromagnetic (EM) environment using computer modeling [1, 2]. The basis of computational electromagnetics applied to modeling the electromagnetic field on objects with a standardized structural-geometrical configuration of design and technological elements is Maxwell's equations in either differential [3–5] or integral forms [4], [6].

• II.    Problem statment

When choosing a method and software for computer modeling, it is necessary to consider not only the basic requirements for mathematical models of the EM field, but also the range of frequencies being modeled, the form of representation of the distribution pattern of the electromagnetic field components, the multi-frequency modeling, and the ability to use the obtained data to generate maps of electromagnetic environmental hazards (based on the criterion of allowable exposure time) [2, 7]. This justifies the need for an extended analysis of known methods of computer modeling of the EM field on objects with radiating sources.

• III.    Theory

The modern approach to solving the system of Maxwell’s equations involves the use of numerical methods [1–3]. Depending on the mathematical framework, the characteristics of the modeled objects, and the problems to be solved in the field of computational electromagnetics, the following widely used calculation methods can be distinguished, which allow modeling the EM environment, as discussed, in particular: the boundary element method (method of moments), the finite element method, the finite difference method in the time domain, and the finite integration method [4–7].

The Finite Difference Time Domain (FDTD) method treats the time dimension in the same way as the spatial dimension [5]. Within this method, the studied portion of space and the time interval are subject to uniform discretization with the specification of initial conditions and the computation of electromagnetic components at the nodes of a structured grid. The advantages of the method, as structurally represented in Fig. 1, include the following:

– the computational operations are performed without using linear algebra hardware [2, 5], limiting the maximum dimension of the problem. This allows for the implementation of large-scale modeling of the spatial distribution of EM fields on objects with volumetric structures.

– operating in the time domain, this method enables obtaining results for a wide range of wavelengths in a single calculation cycle [8] and effectively simulating the electromagnetic field parameters over a broad frequency range, taking into account the spectral composition and superposition of EM fields and radiations.

– the FDTD method allows for the specification of nonlinear, anisotropic, and dispersive media [2], [7], making it suitable for modeling spaces both inside and outside buildings, considering the geometric characteristics of the modeled electromagnetic sources and the electrical properties of materials in the controlled space. Modeled objects and equipment within them are approximated by simple geometric primitives [9], which contributes to accelerated computations.

Despite the wide capabilities of the finite difference time domain method, its main drawback is the limited computational volume of the modeled space, which is usually achieved by assigning artificial boundary conditions [10]. Excessive use of these boundary conditions can lead to significant distortions of the modeled EM field components due to an increase in the computational domain. Therefore, it is impractical to use the finite difference method for large computational volumes [11].

To model the electromagnetic environment using the Finite Element Method (FEM), numerical solutions of the Maxwell’s differential equations with partial derivatives are employed [2, 7]. The

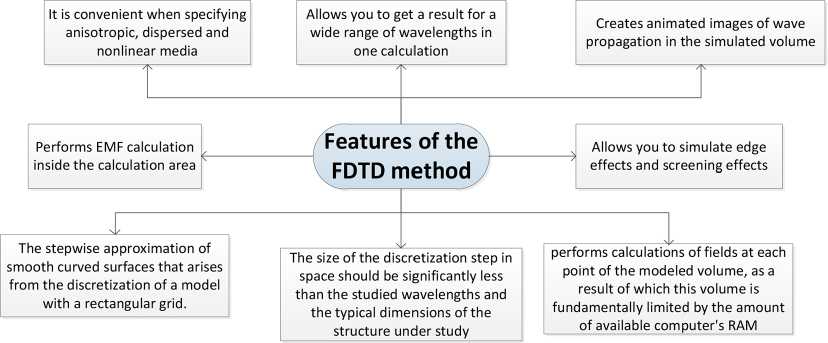
Fig. 1. Features of the FDTD method

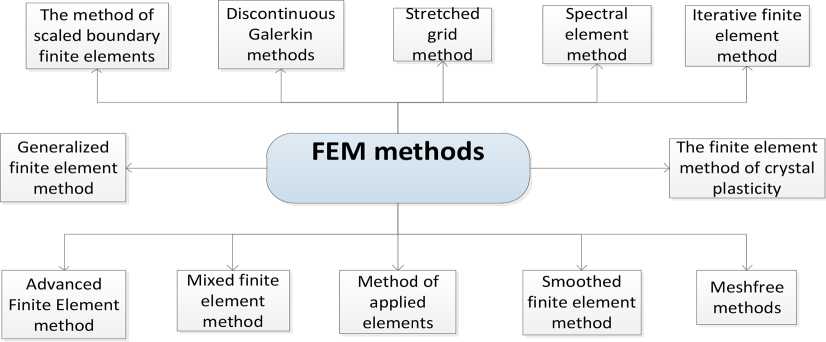
Fig. 2. Varieties of the finite element method essence of this method involves dividing the simulated object into a finite number of subdomains (elements) of rectangular, triangular, or tetrahedral shapes [8]. In each of these elements, an approximating function type is arbitrarily chosen, and its values at the element boundaries (nodes) serve as the solution to the problem and are not known in advance. The modeling process involves a series of computational operations, including the assembly of the so-called Dirichlet and mass matrices, the imposition of boundary conditions on them, and the formulation of a system of linear algebraic equations [6, 12].

The classification of finite element method variations is presented in Fig. 2. Among the most well-known electromagnetic modeling software packages based on this method, HFSS, ANSYS EMAG, and COMSOL Multiphysics can be highlighted [7].

Among the main advantages of the Finite Element Method (FEM), one can highlight the ability to determine EM parameters at any point in the analyzed space and to model volumetric objects with complex geometries and geometrically large and non-uniform electrical bodies [2]. However, this method is characterized by high computational resource requirements, and the simulation duration is the longest among other calculation methods [13, 14].

When using the Method of Moments (MoM), Maxwell’s equations are solved in the frequency domain without specifying boundary conditions. In this approach, discretization is performed only within the framework of a planar computational structure, which does not allow modeling the electromagnetic field in three-dimensional space [8, 13]. The classification of moment’s method variations is presented in Fig. 3.

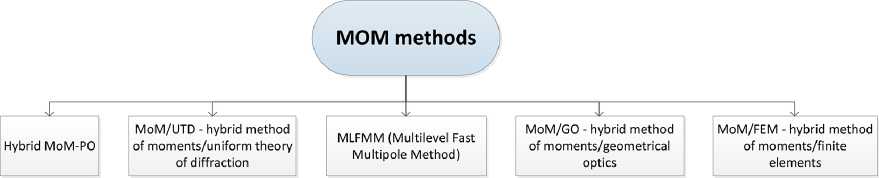
Fig. 3. Varieties of the MoM method

Among the main advantages of the Finite Element Method (FEM), one can highlight the ability to determine electromagnetic parameters at any point in the analyzed space and to model volumetric objects with complex geometries and geometrically large and non-uniform electrical bodies [13], [14]. However, this method is characterized by high computational resource requirements, and the simulation duration is the longest among other calculation methods [2–4].

The separate option of FDTD method is finite integration method (FIT method). FIT method is a discrete formulation of Maxwell’s equations in integral form for numerical solution, defining the calculation domain which is divided into orthogonal cells. A distinctive feature of this method is the ability to calculate multiple materials in a single cell of the computational grid, reducing the number of necessary cells for modeling and shortening the duration of computational operations for generating EM field distribution maps [9, 12].

However, the known software for performing arithmetic, logical, and other operations for monitoring and evaluating the electromagnetic environment does not allow the automated generation of hazard maps under the influence of EM fields across a wide frequency range, taking into account the complex influence using the method of finite integrals [15].

• IV.    Discussion of results

The evaluation of the results of computer modeling is considered on the example of the technological process of pre-sowing seed treatment in an ultrahigh frequency electromagnetic field at a conveyor-type installation. A similar installation for studying the influence of electromagnetic field operating parameters on the quality indicators of buckwheat seeds, developed at the Krasnoyarsk State Agrarian University, is shown in Fig. 4 [16].

As part of the conducted research, volumetric modeling of the electromagnetic environment from a microwave installation was performed using the most common methods. Considering that the adequacy of computer modeling of the considered methods in a narrowly limited calculated volume of

Fig. 4. Installation for seed treatment in a microwave field: 1 – hopper; 2 – microwave chamber; 3 – conveyor belt with cells; 4 – drum; 5 – electric motor the simulated space is almost the same, electromagnetic portraits of several frequency components of the electromagnetic field are formed. Fig. 5 shows an example of modeling the distribution pattern of the energy flux density at a frequency of 2450 MHz, obtained using the finite element method in the Comsol Multiphysics software package. Fig. 6 shows an electromagnetic portrait of the energy flux

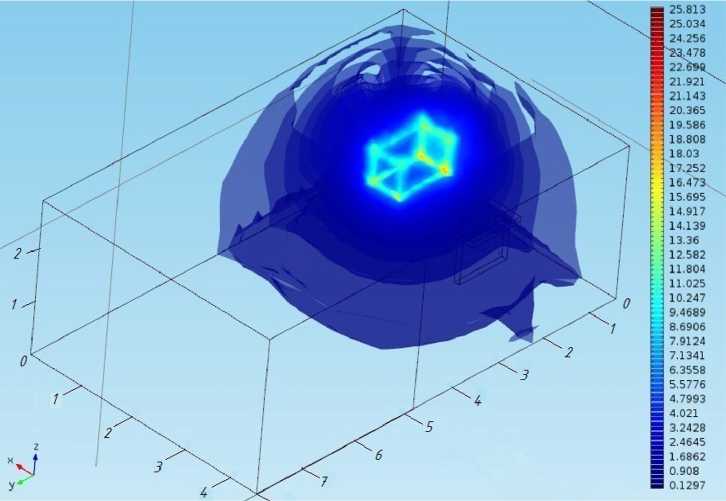
Fig. 5. Picture of the distribution of the energy flux density at a frequency of 2450 MHz, obtained using the FEM method

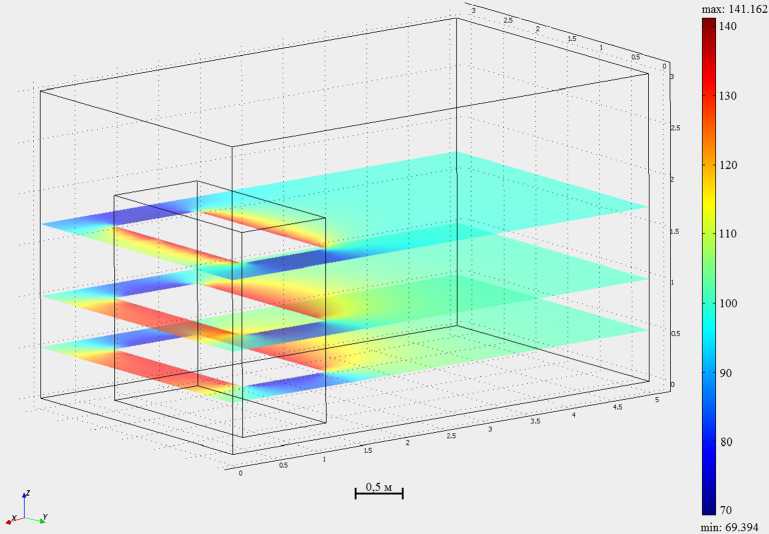
Fig. 6. Electromagnetic portrait of the energy flux density at a frequency of 760 MHz, obtained using the FDTD method

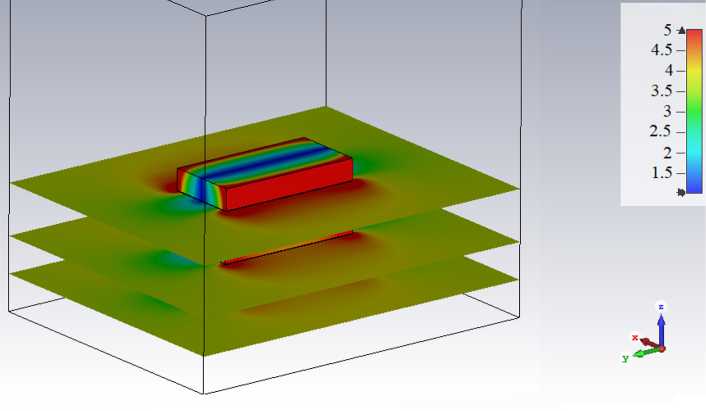
Fig. 7. A three-dimensional picture of the distribution of the electric field (V/m) at a frequency of 3 MHz, obtained using the FIT method density at a frequency of 760 MHz, obtained in the developed software [17] using the FDTD method. Fig. 7 shows a three-dimensional picture of the distribution of the electric field (V/m) at a frequency of 3 MHz, obtained in CST STUDIO using the FIT method.

Based on the analysis conducted, it can be stated that the method of moments requires a larger number of computational operations and does not allow for efficient modeling of electromagnetic fields in three-dimensional space. The method of finite integrals is labor-intensive and therefore impractical for calculating the parameters of EM fields and visualizing hazardous spatial zones. Furthermore, the duration of electromagnetic environment modeling when using this method is only slightly reduced compared to the FDTD method.

• V.    Conclusions

Thus, the finite difference time domain method proves to be the most suitable for modeling the electromagnetic environment both indoors and outdoors, taking into account the complex influence across a wide frequency range and enabling acceleration of the processes involved in generating EM field distribution and hazard maps. This is achieved through the use of established software developed at Altai State Technical University, allowing for the application of the FEM method in modeling complex volumetric objects and geometrically large and heterogeneous electrical structures.