The circumstances in which modular programming becomes the favor choice by novice programmers

Published Online July 2018 in MECS DOI: 10.5815/ijmecs.2018.07.01

The principle of modular design is defined [1] as splitting up large computation into a collection of small, nearly independent, specialized sub-processes. In other words, modular programming is a design principle that divides the functionality of a program into modules each responsible to one aspect of the desired functionality. The modules are independent and can be easily replaced or extended with minimal changes in other modules [2]. Modularity hence supports gradual development, easy maintenance and reusability. To be able to create a modular solution, one needs to possess abstract thinking abilities to deconstruct the solution into logical parts, and then integrate them to create the complete solution. Among the difficulties novice programmers encounter while coping with programming assignments, is the application of the modularity principle in their solutions [3].

The issue of modularity is part of the curriculum of introductory programming course [4]. During this course, students are engaged in problem solving in an increasing level of difficulty. At the beginning of the course, the students learn the basic structures of the programming language, such as variables, conditions, loops etc. Functions and classes are usually taught afterwards. In order to introduce the basic program structures, educators usually use non-modular examples, and give homework assignments in which all aspects of the program are applied in one module. As a result, students acquire "bad habits" of programming when it comes to modular code writing. These habits are sometimes difficult to change even though students learn to program using functions, which enables modular programming. Modular programming necessitates investing considerable mental efforts in pre designing the program, hence the "bad habits" are difficult to cutoff. However, real-world software systems are far more complex than homework assignments, and necessitate modularity for proper functionality and easy maintenance. Nevertheless, people prefer to invest minimal mental efforts in tasks involving problem solving, even if it comes at the expense of the solution's quality [5].

The issue of modularity is part of the curriculum of introductory programming course [4]. During this course, students are engaged in problem solving in an increasing level of difficulty. At the beginning of the course, the students learn the basic structures of the programming language, such as variables, conditions, loops etc. Functions and classes are usually taught afterwards. In order to introduce the basic program structures, educators usually use non-modular examples, and give homework assignments in which all aspects of the program are applied in one module. As a result, students acquire "bad habits" of programming when it comes to modular code writing. These habits are sometimes difficult to change even though students learn to program using functions, which enables modular programming. Modular programming necessitates investing considerable mental efforts in pre designing the program, hence the "bad habits" are difficult to cutoff. However, real-world software systems are far more complex than homework assignments, and necessitate modularity for proper functionality and easy maintenance. Nevertheless, people prefer to invest minimal mental efforts in tasks involving problem solving, even if it comes at the expense of the solution's quality [5].

Proper design requires the recursive dismantling of the solution into modules until it is simple units each responsible to one and only aspect. This recursive process requires abstract thinking and the ability to identify units that can be used to implement multiple functionalities. For this purpose, the unit design should include its structure (e.g., variables, algorithm), its inputs (e.g., parameters), and its output (e.g., return value, exception). Many programmers in general and novice ones in particular, do not invest sufficient efforts in the solution's design, due to lack of experience and skills. As a result, many software systems suffers from lack of modularity at some level [6, 7]. Software that is characterized by poor modularity cause high error rates and costly maintenance [8].

In this paper, we examine the level of code modularity of novice programmers under various conditions. Specifically, we set two goals: (1) Examine the programming style of novice programmers with special focus on modularity depending in the task's level of complexity and in the absence of explicit instructions regarding quality. (2) Examine whether there is a difference in the extent of use of modular programming between a complex task given at once and the same task that is disassembled into simple stages.

To address this aim, we gave two student groups a programming assignment. The first group (hereinafter Group-1) had to address the assignment given in three stages where each successive stage adds requirements to the previous one. The second group (hereinafter Group-2) had to address the same assignment provided at once.

In what follows, we present related works and theoretical background, the study, results and discussion and concluding remarks.

• II.    Related works and Theoretical background

In what follows, we present a brief theoretical background on modularity in programming; dual-process theory; and cognitive dissonance theory.

• A.    Modularity in programming

Modularity in programming refers to a technique design that separates the functionality of a code into independent, extendible, reusable, maintainable and interchangeable modules, each responsible for one aspect of the desired behavior of the program [2] Modular code is obtained by decomposing a problem into sub-problems, and designing a solution for each of them as an independent unit, accompanied by an interface definition for their execution (i.e., parameters, return value, etc.). Afterwards, these units are integrated to achieve the complete solution to the given problem. The above process is recursive in nature because the sub-problems created in the initial decomposition can be broken down again. During the decomposition, software components (e.g., classes, functions) are defined, each with an appropriate interface. Recursive process can be stopped at different stages of dismantling the problem and the deeper the level of decomposition, the more time and efforts required to define the components and their interfaces. In addition, on the "way back", to construct the complete solution, one should invest time and efforts in assembling the components into an integrated whole [9].

The concept of modularity in software systems was widely discussed in the research literature and lack of modularity was found as a source of errors, and costly maintenance [9, 10, 11, 12]. In addition, it was found that modular programming affects the quality of the product in a way that it improves the software's readability and understanding, facilitates maintenance and increases the reuse of the software components [11, 12].

In this study, we examine the level of modularity of code written by novice programmers as a function of the complexity of the problem under examination.

• B.    Dual-process theorey

Dual-process theory deals with the distinction between intuitive and analytical modes of thinking. This theory suggests that human cognition and behavior operate in two different modes, in parallel, called System 1 (S1) and System 2 (S2)[13, 14, 15]. These modes resemble our perception of intuitive and analytical modes of thinking ([16]. These modes are activated by different parts of our brain, and have different evolutionary history. The dualprocess theory refers to S1 thinking processes as being automatic and fast. They are perceived as unconscious, effortless, and inflexible. S2 thinking processes on the other hand, are being effortful and slow. In addition, they are perceived to be conscious, flexible, and expensive in terms of working memory resources. S1 and S2 systems differ mainly on the level of accessibility referring to the easiness and rapidness thoughts come to our mind.

Usually, S1 and S2 systems work hand-by-hand to provide responses adapted to the situation at hand. S1 is usually the first system to be activated and provide response to the current situation. S2 system then, may or may not be activated to monitor and critic S1's responses and override them if necessary. It is sometimes possible to explain people's erroneous answers (usually obtained by activating S1) to certain questions in the failure of activating S2. The dual-process theory is also used to explain problem-solving results obtained in mathematics and computer science education researches [5, 17, 18, 19].

In software engineering, as in mathematics, complex abstract concepts exist. Both domains require a certain amount of analytical rather than intuitive thinking. We find this theory suitable to explain novice programmers' performances referring to the level of modularity in their code.

• C.    Cognitive dissonance theory

Cognitive dissonance refers to the mental discomfort that might occur to an individual who at the same time holds two or more incongruous beliefs, ideas, or values. The occurrence of cognitive dissonance is a consequence of a person performing an action that contradicts personal beliefs, ideals, and values; and it can also happen when one is confronted with new information that contradicts her beliefs, ideals, and values [20, 21].

Leon Festinger (1957) established the Theory of Cognitive Dissonance, which refers to human tendency to strive for internal psychological consistency in order to mentally function in the real world. An individual who experiences internal inconsistency tends to become psychologically uncomfortable, and is motivated to reduce the cognitive dissonance. This can be achieved by making changes in the stressful behaviour, either by adding new information to the cognition causing the psychological dissonance to reduce the dissonance, and/or by actively avoiding contradictory information likely to increase the degree of the cognitive dissonance.

In the context of this study, we provide the students with a problem decomposed into stages each adds requirements to the previous one. The solution of each stage may or may not rely on the solution of the previous stage. Using the previous stage's solution is tempting since it requires fewer efforts than redesigning and rewriting the entire solution. Nevertheless, such course of solution results in code duplication and hence non-modular solution. This situation might raise a conflict, within this study we examine the ways students dealt with this conflict, and we use the dissonance cognitive theory to analyse their behaviour.

• III.    The Study

In what follows, we present information regarding the study participants, the data collection and analysis methods, and results with discussion.

• A.    The study participants

  The data were collected during the academic years 2017-2018. The study participants were third (and final) year Information Systems students in an academic college in Israel. Forty students participated in the research, All the participants were graduated from the following programming courses: "Introduction to computer science", and "Object oriented programming". In these courses, the students were exposed to the advantages of code modularity and its effects in both procedural and object oriented paradigms. The modularity was practiced via many courses' assignments. Out of these forty students, 12 were females.

To address the research aims, the participants were randomly assigned into two groups. The two groups (20 students in each) had to provide solution to the same programming assignment, which was presented to them in two different ways. The assignment was presented to the first group divided into three successive stages (See Fig. 1) each given after the completion of the previous. The second group had to address the same programming assignment, presented as a whole task (See Fig. 1). Both groups were given no specific guidelines other than the requirement to provide a solution in any programming language they deem fit.

• B.    The course of the study

In this section, we elaborate on the programming assignment (two versions), its expected modular solution, collection of data and analysis tools.

• 1)    The problem

The problem provided to the first group of the study participants is shown in Fig 1. They first had to address stage 1's requirements, and upon delivery of their solution, each student was given stage 2's requirements, followed by stage 3's requirements. The study participants of the second group were provided with the entire problem shown in Fig. 1, without separation to stages.

A good possible solution is presented in Fig. 2. The solution is considered modular, clear, and reusable. As shown, it includes two classes. One, class Polynomial (Fig. 2a) representing the Polynomial function and the other, class Program (Fig. 2b) represents the program, which uses it.

The Polynomial class has an array of coefficients with a constructor to initialize them. In addition, a method for each utility specified in the requirements: (1) evaluating the polynomial at point x; (2) building the derivation polynomial; (3) formatting a string to represent the polynomial; (4) testing for zero polynomial; (5) getting highest degree of the polynomial. In addition, two extra utility methods are defined, to support the implementation of the toString() method, one for the formatting of a coefficient, and second for the formatting of the degree of each component of the polynomial.

Stage 1:

You are asked to write a program (Java, or pseudocode) that takes the following input: (1) positive integer n referring to the highest degree of a polynomial function; (2) n+1 real numbers referring to the coefficients of that function; (3) additional real number x .

To remind you, a polynomial function of degree n: f(x) = a _n x ⁿ + a _n-1 x ^n-1 +^+ a 1 x 1 + a ₀ x ⁰

Then, the program evaluates the value of the given polynomial function at point x and prints the result. Herein, an example of a run:

Polynomial function's degree: 4

Coefficient of X ⁴ : 3

Coefficient of X ³ : -7

Coefficient of X ² : 0

Coefficient of X ¹ : 1

Coefficient of X ⁰ : -5

Provide x-value: 10

Evaluation of 3X ⁴ -7X ³ +X-5 at 10.0 is 23005.0

Stage 2:

In addition to the requirements of the previous task, the program has to compute also the derivative of f(x), that is f'(x), and evaluates its value at point x and prints the result.

To remind you, a the derived polynomial function of f(x) = a _n x ⁿ + a _n-1 x ^n-1 +...+ a 1 x 1 + a ₀ x ⁰ is calculated as f (x) = na _n x ^n-1 +(n-1)a _n-1 x ^n-2 +(n-2)a _n-2 x ^n-3...+ a 1

Herein, an example a run (following the previous printouts):

Evaluation of 12X ³ -21X ² +1 at 10.0 is 9901.0

Stage 3:

In addition to the requirements of the previous tasks, the program has to compute also the second, third, etc derivative polynomials of f(x), evaluates their values at point x and prints the results.

Herein, an example a run (following the previous printouts):

Evaluation of 36X ² -42X at 10.0: 3180.0

Evaluation of 72X-42 at 10.0: 678.0

Evaluation of 72 at 10.0 is 72.0

Fig.1. The problem.

• 2)    The problem's solution

The solution presented in Fig. 2 is modular since it is composed of several components, each responsible for one aspect of the requirements. Fixing a bug, replacing an algorithm (e.g., different printout, another form of derivation) or adding extra functionality is easy, since it requires the change of only one method, and does not require re-implementation of other methods. This solution is also clear, enabling its understanding even with the absence of documentation. Upon maintenance, it is easy to locate the code segment that requires a change, make the change, and test it with isolation from the rest of the code. It is also easy to add new methods (e.g., integral, adding) since it does not require any change in existing methods. Moreover, the implementation of a new method may be achieved via the use of existing methods, avoiding code duplications. This solution also supports reusability, as the Polynomial class is independent of the Program class, and hence can be taken to new systems and be used in other contexts, without dragging irrelevant code.

• C.    Data collection and analysis tools

The aim of the study was to explore the circumstances in which novice programmers consider modular design while developing software solutions, and the underlying reasons. Hence, we used qualitative research methods. During the study, we used various research tools to collect and analyze data in order to perceive a comprehensive yet in depth and particular overview regarding the above aim.

The data were comprised of the students' solutions of the given programming assignment from both student groups. During the review of the students' solutions, we classified each solution of every stage into three main categories: 1-non-modular, 2-partial-modular, 3-full-modular. In the first category, we classified solutions in which the entire code was written in one or two methods in a single class. In the second category, we classified solutions in which only one class exists, however, several methods are defined, each responsible for few aspects. In the third category, we classified solutions that resemble the modular solution (Fig. 2), in the sense that it contains a Polynomial class separated from the main class (program) that includes several methods.

Then we conducted open interviews with all the participants in which we asked them to elaborate on the reasons and motivations underlying their solutions with special focus on modularity.

In the data analysis process, we interpreted the research data through the dual process theory [14, 13, 22]. We also used concepts of cognitive dissonance theory (Fetinger, 1957, Cooper, 2011) to interpret the obtained results. In addition, we used content analysis methods [23, 24] to examine the impact of the assignment formulation on the level of modularity of the solution.

• IV.    Results and Discussion

In this section, we present the students' solutions (of both groups) and compare the differences between the levels of modularity in each. Then we discuss the findings and analyze them using the dual process and the cognitive dissonance theories.

public class Polynomial{ private double[] coefficients ;

public Polynomial( double [] coefficients) { this .coefficients = coefficients;

} public double evaluate(double x) { double sum = 0.0;

• sum += coefficients[i]*Math. pow (x, i);

return sum;

} public String toString() {

String str = "";

// first coefficient handled outside loop because of the sign str += formatCoefficient(coefficients[degree()]);

str += formattedDegree(degree());

for ( int i = degree()-1; i >= 0; i--){ if (coefficients[i] == 0.0)

continue ;

str += (coefficients[i] > 0.0)? "+":"";

str += formatCoefficient(coefficients[i]);

str += formattedDegree(i);

} return str;

} private String formatCoefficient(double d) { if (d==0.0 || d==1.0) return "";

else if (d == ( int )d) return ""+( int )d;

else return ""+d;

} private String formattedDegree(int i) { if (i==0) return "";

else if (i==1) return "X";

else return "X^"+i;

} public Polynomial derivate() { double[] derivativeCoefficients;

derivativeCoefficients[i - 1] = i * coefficients[i];

return new Polynomial(derivativeCoefficients);

}

}

Fig.2(a). The modular solution – Polynomial Class.

public static void main(String[] args) {

Polynomial p = acceptPolynomial ();

double value = acceptValue ();

do { evaluate(p,value);

p=p.derivate();

} while (!p.isZero());

} private static double acceptValue() {

+ " is " + value + ":"+ p.evaluate(value));

} public static Polynomial acceptPolynomial() {

int n = input .nextInt();

double [] coefficients = new double [n+1];

for ( int i=n; i>=0; i--) {

coefficients[i] = input .nextDouble();

} return new Polynomial(coefficients);

}

}

Fig.2(b). The modular solution – Program Class.

• A.    Group 1 – stage 1

At the first stage, the students were asked to write a computer program that gets input of a polynomial function that includes the degree of the polynomial, its coefficients and x-value (Fig. 1). The program evaluates and prints the polynomial's value in the given point x. Classifying the solutions to the above categories revealed that 85% were non-modular, 10% were partial-modular, and only 5% were modular.

The majority of the students provided a non-modular solution (Fig. 3). This solution addresses all the problem's requirements in one method. It includes a single class with a main method containing the code segments for handling the user input, initializing the polynomial coefficients and calculating the polynomial value at the given point. This code suffers from lack of clarity, and impossible for reuse. To understand the code, one must read it carefully and follow many line of noncohesive code. The code cannot be reused because it is built as a single unit. It is worth noting that none of the non-modular solutions dealt with the formatting of the polynomial output according to example given in the problem text (i.e., positive vs. negative coefficient, coefficient with zero or one value vs. other values, zero or one degree vs. other degrees). Instead, they output the polynomial component as is.

At this point, the students did not know that they might be required to use what they have already done at this stage, and therefore did not set the goals of modularity, clarity and reusability for themselves. From their point of view, they dealt with a specific task, and their solution met their own expectations regarding the required solution. The following excerpt is taken from the interviews conducted with the students. It reflects the students' thoughts in similar words:

" Why not use a modular solution? Good question. I did not really think about it. This looks like a specific task and we learned that a modular solution is effective when a generalization is required. If I knew there were follow-up tasks, I might have done a modular solution ."

In terms of the dual-process theory [14, 13, 22], we might say that the students did not activate S2 but instead turned to S1, which employs intuitive considerations. Activating S1 saves cognitive efforts. To be able to design a modular solution, the students had to demonstrate abstraction abilities and high programming skills. For novice programmers, these skills are not yet intuitive part of their professional toolbox and hence had to activate S2 in order to come with a modular solution. In the absence of explicit instructions regarding the desired quality of the solution, the students' goal is to deliver a solution that addresses the problem with minimal efforts investment. For that purpose, they implemented the first solution came to mind (activate S1) and were satisfied with the results. Minimal investment of mental efforts results in none modular solution as it avoids pre-design. This pattern of behavior is more common among novice programmers, which lack the understanding of the importance of modularity and thus concentrating on the shortest path to satisfactory solution.

It is worth noting the only student who provided a modular solution was an experienced programmer.

public class Program { public static void main(String[] args) {

// getting user input and initializing coefficients

int n = input.nextInt();

double [] coefficients = new double [n+1];

for ( int i=n; i>=0; i--) {

coefficients[i] = input.nextDouble();

}

}

}

Fig.3. Non-modular solution – stage 1

• B.    Group 1 – stage 2

In this stage, the students were asked to write a computer program that in addition to the requirements from the previous stage, requires the derivation of the given polynomial and computes the derivative's value at the given point x (Fig. 1). The students were provided with their previous stage solutions after we took a snapshot of them.

The classification of the students' solutions of this stage revealed that 75% were non-modular, 15% were partial-modular, and only 10% were modular. At this stage, majority of students still adhere to the non-modular solution (Fig. 3). As shown, they proceeded with the solution from the point where it ended in the previous stage, adding more lines of code in the main method, including code duplications. However, two students had improved their solution. One of them rewrote his solution and built a separate class to represent the polynomial function, and the other change the code structure by dividing the main method into several methods.

Among the other students who kept the course of non-modular solution, buds of understanding as regards to the need for modular problem was raised. Nonetheless, since they have already solved the first part in a non-modular way, they chose to continue with the same course of solution in order to avoid solving the problem from the beginning. In other words, at this stage we can see a start of understanding that a modular solution is more suitable, but laziness still prevails, and only 10% of students improved their solution. The following excerpt from the interviews reflects the students' thoughts as regards to the solution of the second stage (none modular) in similar words:

" In fact, it occurred to me that the code for the evaluation of the derivative polynomial is identical to part of the code I wrote earlier. However, since I already had a solution to the previous stage, it seemed a waste of efforts to rewrite the solution. Therefore, I decided to continue without changing the code from earlier stage."

From the above excerpt, we can learn that there was a dilemma between focusing their efforts in the new assignment and providing a satisfactory solution, as fast as possible (activating S1), and redesigning the entire solution of both stages (activating S2) to avoid code repetitions and improve modularity and clarity. The majority of the students preferred the first alternative to avoid greater cognitive efforts. In terms of dissonance cognitive theory (Cooper, 2011), we may say that the problem of this stage created a cognitive dissonance, and to overcome these stressful feelings, they justified their modus operandi in that it was a waste of time and effort to write the solution from the beginning without explicit requirements for modularity.

• C.    Group 1 – stage 3

In this stage, the students were asked also to calculate all the remaining derivative polynomials of the original one and computes their values at the given point x (see

Fig. 1). The students were provided with their previous stages solutions after we took a snapshot of them.

The classification of the students' solutions of this stage revealed that 60% were non-modular, 25% were partial-modular, and only 15% were modular. Three additional students redesigned their solutions at this stage and provided modular (or partial-modular) solutions. Still, majority of the students chose to invest minimal efforts in solving the task and avoid redesigning the entire solution.

public class Program { public static void main(String[] args) {

// same as phase 1

...

double [] derivativeCoefficients = new double [n];

sum = 0.0;

derivativeCoefficients[i - 1] = i * coefficients[i];

// calculating the polynomial value

}

}

Fig. 4. Non-modular solution – stage 2

The partial modular solution (Fig. 5) includes several methods in one class. In the majority of the solutions classified as partial-modular, we found methods for (1) user input; (2) evaluating the polynomial at the given point; (3) deriving a polynomial; etc. However, the methods themselves are partial-modular. For example, the derivate() method in Fig. 5 includes many commands: (1) creating an array of coefficients for the derivative function (2) calculating the coefficients (3) evaluating the derivative function at point x (4) printing the polynomial itself and the evaluation results. The derivate() method could be further divided into smaller, cohesive logical units, each responsible for a single operation. Clearly, the partial-modular solution (Fig. 5) is less clear and more difficult to reuse than the modular solution (Fig. 2).

During the interviews, one of the few students that changed their solution from non-modular to partial-modular stated:

" At this stage I noticed that repeated actions of polynomial derivation had to be done a second time and I saw that the code I wrote for the previous stages began to be cumbersome with lots of repetitions. Therefore, I decided to write a function that calculates the derivative and avoid some of these repetitions. If I would get the entire problem from the start, I might design and implement the derivative method from the start ".

The following excerpt was stated by one of the students who did not changed their solution:

"At this stage it became obvious to me that the continuing with the same course of solution will lead to many code repetitions. However, I did not consider redesigning since I wanted to complete the task as fast as possible, having in mind that the achieving a solution that solve the problem is the most important criterion."

At stage 3, in which the entire problem was revealed to the students, most of the students who solved the previous stages in a non-modular way came to realization that their course of solution was problematic (code repetitions, unclear). In terms of the dual-process theory [14, 13, 22], we may say that when receiving new information that do not support the previous choices regarding the course of solution, S2 was activated and a cognitive dissonance [20, 21] was created. The cognitive dissonance stems from the students' understanding that the solution they chose is problematic in that it requires repeatedly writing the same code for calculating the following polynomial derivatives, which contradicts the planning principles they have learned. In order to solve the dissonance, most of them chose to continue the course of solution they had chosen earlier, and attributed their choice to their desire to complete the assignment quickly. In contrast, few students have chosen to solve the cognitive dissonance by changing the course of solution into a more modular one. They realized that the quality principle is sufficiently important and hence cannot be ignored.

From the students' interviews, we concluded that giving the problem in stages makes it difficult for novice programmers to plan an optimal solution (modular) right from the beginning, but rather to focus on a specific, non-modular solution of each part separately. Moreover, when they already got all parts of the problem, they were not motivated to change the course of solution and throw stages. away the code they had already wrote for the previous public class Program { public static void main(String[] args) {

int n = input.nextInt();

double [] coefficients = new double [n+1];

for ( int i=n; i>=0; i--) {

coefficients[i] = input.nextDouble();

}

double x = input.nextDouble();

evaluate (coefficients, x);

derivate (coefficients, x);

} private static void evaluate(double[] coefficients, double x){ double sum = 0.0;

derivativeCoefficients[i - 1] = i * coefficients[i];

coefficients = derivativeCoefficients;

n--;

double sum = 0.0;

evaluate (coefficients, x);

}

}

}

Fig.5. Partial modular solution

At each stage, more information is added that makes it difficult for the students keep the non-modular course of solution and in fact increases the cognitive dissonance they experienced. However, since in early stages they chose to resolve the cognitive dissonance by justifying their course of non-modular solution with the problem character being concrete and simple one, in the successive stages they continue to justify their choice by providing additional excuses as minimal time investment yet providing a solution that address the problem requirements regardless quality.

• D.    Group 2 – Entire problem

The students in this group were given the entire assignment, which is composed of all the parts given to the first group (Fig. 1). They were also given no further instructions as regards to the nature of the desired solution.

The classification of the students' solutions of this stage revealed that 30% were non-modular, 40% were partial-modular, and only 30% were modular.

The students, who provided a modular solution (Fig. 2), asserted the following excerpt it similar words:

"When I read the problem it occurred to me right away that many calculations of polynomials are required. Hence, I created a polynomial class to contain all the necessary methods, just as we learned in object-oriented programming course. It was not a difficult task for me."

The students who provided partial modular solution asserted in similar words:

" When I read the problem, I identified repeated elements such as the polynomial derivation and the calculation of its value. However, it was difficult for me to design a perfect solution that included many classes and methods. I did my best to finish the task successfully. "

As to the students who provided non-modular solution, they justified it in similar words:

"As I progressed with my solution, I saw that it contains many code repetitions. But you [the researchers] didn't specified any criteria as regards to the quality of the solution, so I decided to invest the minimal efforts and come with a working solution… to provide a modular solution, it would have taken me longer time to achieve."

Evolution of modularity

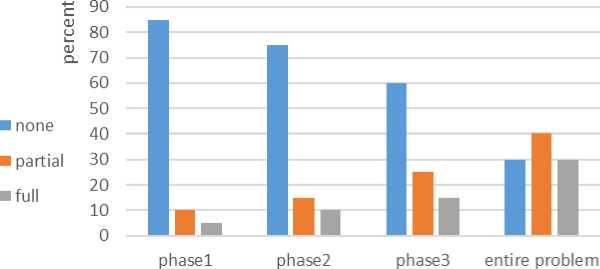
Fig.6. Evolution of modularity

From the above excerpts, we can learn that though the students received the same entire problem, each of them interpreted it differently according to their abilities and skills. Thirty percent of the students were able to identify the problem components, and define appropriate classes and methods to address them. From the first excerpt it can be learned that there are students who have internalized the importance of early planning of the solution, which eventually leads to a modular one. Yet, it was important for these students to provide a solution in a short time. They realized that investing time in planning the solution would lead to savings in coding time and result in a short and clear solution. The internalization of the importance of the designing stage before coding can indicate on abstraction abilities and planning skills. We may infer that the planning stage has become an integral part of the student's cognitive toolbox. In terms of dual-process theory, we may say that for these students, modular solution is achieved by activating S1.

Forty percent of the students provided partial-modular solutions. From the second excerpt, we learn that these students understand the advantages of modular design but encounter difficulties in its implementation. In terms of the dual-process theory, we might infer that modular design is not becoming completely an integral part of S1.

Thirty percent of the students were not able to grasp the problem as a whole, and instead they view it as a collection of sub-problems each to be addressed separately and successively, similar to the situation of the first group, which received the problem in stages. In terms of dual-process theory, we might infer that these students were not able yet to integrate modularity into their S1. This may be attributed to several reasons. The first reason is related to the cognitive efforts they are required to invest while planning a modular solution. Tough the students studied and practiced the concept of modularity in several courses; they were not necessarily exposed to the consequences of non-modular code. Namely, they were not required to change such code in order to add functionality or fix bugs in it. As a result, the modularity principle was not internalized completely. For some of them, it was not internalized at all, and remained hollow slogan. In addition, the students got used to address assignments that include explicit and detailed instructions. In the absence of such instructions, they set criteria of their own, which do not necessarily include modular considerations and pre-design. As a result, the importance of concepts such as modularity is not internalized and do not become a natural part of the cognitive toolbox.

• E.    Comparative analysis

Fig. 6 demonstrates the evolution of modular solutions across the stages of group-1 and the distribution of solutions of group-2.

As to group-1, it might be said that the number of non-modular solutions decreases from stage to the next stage, but remains high even after the third stage in which the entire problem was revealed to the students. As to group-2, 70% of the students provided partial or full modular solution and only 30% of them provided non-modular solutions. Comparing group-1-stage 3 with group-2 distributions reveals that although at this point both groups had the entire problem, there is a significant difference between the non-modular solutions among the groups. The difference between the groups may stem from the fact that the students of group-2 had the entire problem right from the beginning and were exposed to the complexity of the problem, while the students of group-1, had to cope with a simple problem that was getting complicated in each consecutive stage. Group-2' students were able to plan a solution that addresses all parts of the problem, identify the code repetitions and avoid them using modular design. Group-1's students, on the other hand, had to address a simple task at the first stage, without knowing the future requirements. Even when they got the additional requirements in successive stages, most of them kept their previous course of solution, while handling the new requirements as a patch, without changing the code written beforehand.

It is worth noting that among group-2's solutions, 30% provided non-modular solutions although exposed to all the requirements at the beginning. Many of them justified their behavior by asserting that no specified criteria as regards to the quality of solutions was set, hence they chose the fastest path to come with a working solution. Some of them asserted that retrospectively they understand that modular solution could save time by avoiding code repetitions, however, when coping with the task it did not occur to them.

• V.    Implications to Instruction

• VI.    Concluding Remarks

In this study, we explored the level of modularity in code produced by novice programmers. The research data revealed that when a problem includes several functionalities that have to be addressed with repetitive operations, more students turn to modular programming, although it was not easy for them. Modular programming requires abstraction and generalization skills to be able to design the solution before implementation. This is especially difficult when novice programmers are involved. However, when the same problem is give as a collection of simple sub-problems given successively, the vast majority of students tend to solve the problem in a non-modular way. This tendency might be explained via dual-process theory [14, 15, 25] that asserts that natural tendency of people is to invest minimal efforts in solving problems they are confront with (activating S1). We also found that even after they understand that a modular solution would fit better, a situation, which evokes cognitive dissonance [20, 21], they adhere the original course of the solution. To overcome the cognitive dissonance, many of them assert that it seems ineffective and a waste of time to "throw away" what they have done so far and start all over again.

In a follow-up study, we intend to apply the recommendations specified in the "Implications to instruction section", and examine its effect on the students' programming style.

In order to gain further refined insights, this study should be repeated with large groups of students separating them according to academic achievements, and compare their performances to products of experienced programmers.