The Construction of two classes of 4-valent tri- Cayley Graphs over Cyclic Group

Автор: Xiaohan Ye, Huanzhi Zhang

Журнал: International Journal of Mathematical Sciences and Computing @ijmsc

Статья в выпуске: 1 vol.10, 2024 года.

Бесплатный доступ

The symmetry of the graph has always been a hot topic in graph theory and the vertex-transitive graphs are a class of graphs with high symmetry. Cayley graphs which are the highly symmetrical graphs play an important role and much work has been done in the study. The tri-Cayley graph is a natural generalization of the Cayley graph. A graph is said to be a tri-Cayley graph if it admits a semiregular subgroup of automorphisms having three orbits of equal length. Koács et al. classified the cubic symmetric tricirculants in 2012 and Potočnik et al. classified the cubic vertex-transitive tricirculants in 2018. Currently, there is no research on the classification of 4-valent tri-Cayley graphs over cyclic group. In this paper, we will construct two classes of 4-valent tri-Cayley graphs over cyclic group and discuss their automorphism groups. In addition, the vertex transitivity, edge transitivity and arc transitivity are proved.

Еще

Tri-Cayley graph, cyclic group, vertex-transitive, automorphism group, edge-transitive, arc-transitive

Короткий адрес: https://sciup.org/15019070

IDR: 15019070 | DOI: 10.5815/ijmsc.2024.01.01

Текст научной статьи The Construction of two classes of 4-valent tri- Cayley Graphs over Cyclic Group

All groups considered in this paper are finite, and all graphs are finite, connected, simple and undirected. For the group-theoretic and graph-theoretic terminology not defined here we refer the reader to [1,2].

A graph is said to be a tri-Cayley graph if it admits a semiregular subgroup of automorphisms having three orbits of equal length. Note that every tri-Cayley graph admits the following concrete realization. Let A , A , A , R , R and R be subsets of a group G with identity element e such that A = A ¹, A = A ^- ¹, A₂ = A - and e £ A о A о A . Then we let X = TCay( G ; A , A , A ; R , R , R ) be the graph with vertex set Z₃ x G , and edge set the union of ^{{(0, g ^),(0, a 0 g Wl a 0 ^e A 0 ^} , ^{{(0, g ^),(1, ^r 0 g ^)} ^r 0 ^e R 0 ^} , {{(1, g Ш a 1 g ^)} a 1 ^e ^A 1 ^} , ^{{(1, g ^),(2, ^r 1 g ^)} r ^e R 1 ^} ,

{{(2, g ),(2, a ₂ g )|| a ₂ e A ₂} and {{(2, g ),(0, r ₂ g )|| r ₂ e R ₂} . For the case when | R 0 1 = | R 1 | = | R 2 1 = 1, Tcay

( G ; A , A , A ; R , R , R ) is also called one-matching tri-Cayley graph. Also, if | A | = | A | = | A | = s , then Tcay ( G , A , A , A ; R , R , R ) is said to be an s -type tri-Cayley graph.

The tri-Cayley graph is a natural generalization of the Cayley graph, which was proposed by Kutnar et al. [3] when they studied the the structure of strongly regular tri-Cayley graphs and gave a structural description of strongly regular tri-Cayley graphs of cyclic groups. The symmetry of the tri-Cayley graph has also been a hot topic, and the main research focus being on classifying tri-Cayley graphs with specific symmetry properties over a given finite group. In recent years, the main research focus being on classifying tri-Cayley graphs with specific symmetry properties over cyclic group. For example, in [4], it gave that the complete bipartite graph K , the Pappus graph, Tutte’s 8-cage and the unique cubic symmetric graph of order 54 are the only connected cubic symmetric tricirculants; all finite connected cubic vertex-transitive tricirculants were classified in [5].

Moreover, it is well known that the symmetric graph is an important graph not only in algebraic graph theory, but also has a wide range of applications in real life. For example, more efficient algorithms can be realized by using the symmetry of the graph in the field of the Internet models. Therefore, it is necessary for us to study the vertex-transitive graphs. Marušič and Pisanski [6] classified the cubic edge-transitive bi-Cayley graphs over cyclic group. Boben et al. [7] studied some properties of the cubic 2-type bi-Cayley graphs over cyclic group. For additional results regarding the biCayley graphs over cyclic group we refer the reader to [8-11]. The bi-Cayley graphs over abelian group were also studied, and for results about it, we refer the reader to [12-14]. Later, the bi-Cayley graphs over finite groups with more complex structures were further studied. For example, cubic symmetric bi-Cayley graphs on nonabelian simple groups were classified and the full automorphism groups of these graphs were determined in [15]; trivalent vertex-transitive biCayley graphs over dihedral groups were classified and Cayley property of trivalent vertex-transitive bi-dihedrants was presented in [16]. Currently, there is no research on the classification of 4-valent tri-Cayley graphs over cyclic group. In this paper, we will construct two classes of 4-valent tri-Cayley graphs over cyclic group and discuss their automorphism groups. In addition, the vertex transitivity, edge transitivity and arc transitivity are proved.

2. Research Method

All the necessary definitions, some preliminary results and the most basic Lemma 3.4 are presented in Section 3. According to the definition of tri-Cayley graph and Lemma 3.4, we will construct two classes of 4-valent tri-Cayley graphs over cyclic group. Next, we will discuss their automorphism groups and the vertex transitivity, edge transitivity and arc transitivity are proved in Section 4 and Section 5.

3. Definition and Preliminaries

For a finite, connected, simple and undirected graph X , we use V ( X ), E ( X ), A ( X ),Aut( X ) to denote its vertex set, edge set, arc set and full automorphism group, respectively. A graph X is said to be vertex-transitive , edgetransitive and arc-transitive (or symmetric ) if Aut( X ) acts transitively on V ( X ), E ( X ) and A ( X ), respectively. In a graph, we denote that N ( v ) is the set of vertices at a distance of i from the vertex v , called the i-step neighborhood of the vertex v . Especially, N ( v ) is the set of all vertices adjacent to v . We denote that z is the cyclic group of order n . Let G be a permutation group on a set Ω and α ∈ Ω , the vertex-stabilizer of α in G is denoted by G _α = { g ∈ G ∣ α ^g = α }, that is, the subgroup of G fixing the vertex α .

In this section, we always assume that X = TCay( G ; A , A , A ; R , R , R ) is a connected tri-Cayley graph over a group G . To study the content of Section 4 and Section 5, we give the following definition and preliminaries.

Definition 3.1 For any i ∈ = {0,1,2} and g , h ∈ G , we define R ( h ) :z × G × G by

R ( h ): ( i , g ) ( i , gh ). (1)

It is easy to see that R ( h ) R ( h ′ ) = R ( hh ′ ) . Set R ( G ) = { R ( h ∣ ) h ∈ G } . Then R ( G ) is semiregular subgroup of Aut( X ) isomorphic to G .

Lemma 3.2 ([17]) If there is a finite group G acting on the finite set Ω and α ∈ Ω , then we have

| α ^G | = | G : G α |. (2)

Lemma 3.3 If X = TCay(G; A ,A ,A ;R ,R ,R ) is a connected tri-Cayley graph over a group G , then at most one of R , R and R is empty.

Lemma 3.4 The following hold.

(1) Up to graph isomorphism, if R ≠ ∅ , then R can be chosen to contain the identity element of G , where i = 0,1,2.
(2) G is generated by A ∪ A ∪ A ∪ R ∪ R ∪ R .

Proof: (1) By Lemma 3.3, without loss of generality, let R = ∅ . Take r , r ∈ R , r ′ , r ∈ R . Let X = TCay( G ; A , A , A ; R , R , ∅ ) and Y = TCay( G ; A , r ^- ¹ Ar , r ′^- ¹ Ar ′ ; r ^- ¹ R , r ′^- ¹ Rr , ∅ ) , we define

ρ : V ( X ) V ( Y ) by

ρ : (0, g ) (0, g ), (1, g ) (1, r ^- ¹ g ), (2, g ) (2, r ′^- ¹ g ). (3)

It is easy to see that ρ is a bijection.

If {(0, g ),(0, a ₀ g )} ∈ E ( X ) , then a ₀ ∈ A ₀. It follows that {(0, g ),(0, a ₀ g )} ^ρ = {(0, g ),(0, a ₀ g )} ∈ E ( Y ).

If {(0, g ),(1, r ₀ g )} ∈ E ( X ) , then r ₀ ∈ R ₀ and so r ^- ¹ r ₀ ∈ r ^- ¹ R ₀. It follows that {(0, g ), (1, r ₀ g )} ^ρ = {(0, g ),(1, r ^- ¹ r ₀ g )}

∈ E ( Y ).

If {(1, g ), (1, a g )} ∈ E ( X ) , then a ∈ A and so r ^- ¹ a r ∈ r ^- ¹ Ar . It follows that {(1, g ),(1, a g )} ^ρ = {(1, r ^- ¹ g ),(1, r ^- ¹ a g )} = {(1, r ^- ¹ g ),(1, r ^- ¹ a ₁ rr ^- ¹ g )} ∈ E ( Y ).

If {(1, g ),(2, rg )} ∈ E ( X ) , then r ∈ R and so r ′^- ¹ rr ∈ r ′^- ¹ R r . It follows that {(1, g ),(2, rg )} ^ρ = {(1, r ^- ¹ g ),(2, r ′^- ¹ r ₁ g )} = {(1, r ^- ¹ g ),(2, r ′^- ¹ r ₁ rr ^- ¹ g )} ∈ E ( Y ) .

If {(2, g ), (2, a g )} ∈ E ( X ) , then a ∈ A and so r ′^- ¹ a r ′ ∈ r ′^- ¹ A r ′ . It follows that {(2, g ),(2, a g )} ^ρ = {(2, r ′^- ¹ g ), (2, r ′^- ¹ a g )} = {(2, r ′^- ¹ g ),(2, r ′^- ¹ a r ′ r ′^- ¹ g )} ∈ E ( Y ) . Therefore, X = TCay( G ; A , A , A ; R , R , ∅ ) ≅ Y = TCay( G ; A , r ^- ¹ Ar , r ′^- ¹ A r ′ ; r ^- ¹ R , r ′^- ¹ Rr , ∅ ) . The following is discussed in four cases:

(i) If 1 ∈ R and 1 ∈ R , then the conclusion clearly holds.
(ii) If 1 ∈ R but 1 ∉ R . We know that R ≠ ∅ , it follows that there exists r ∈ R . Thus, 1 ∈ r ^- ¹ R = { r ^- ¹ ∣ s s ∈ R } .
(iii) If 1 ∈ R but 1 ∉ R . We know that R ≠ ∅ , it follows that there exists r ′ ∈ R . Let r = 1 ∈ R , then 1 ∈ r ′^- ¹ R r = r ′^- ¹ R = { r ′^- ¹ ∣ t t ∈ R }.
(iv) If 1 ∉ R and 1 ∉ R . We know that R ≠ ∅ , it follows that there exists r ∈ R . Thus 1 ∈ r ^- ¹ R = { r ^- ¹ ∣ s s ∈ R } . And X = TCay( G , A , A , A ; R , R , ∅ ) ≅ Y = TCay( G , A , r ^- ¹ Ar , r ′^- ¹ Ar ′ ; r ^- ¹ R , r ′^- ¹ Rr , ∅ ), then 1 ∈ R . Therefore, the case (iv) becomes (iii). The result then follows.
(2) Because X is a connected tri-Cayley graph, then for each g ∈ G , it follows that there exists a walk connecting (0,1) to (0, g ) . For any a ∈ A , r ∈ R , a ∈ A , r ∈ R , a ∈ A , r ∈ R , by the (1) of the Lemma, we have

{(0,1),(2,1),(0, r ₂),(1, r ₂),(2, r ₁ r ₂),(0, r ₁ r ₂),(1, r ₀ r ₁ r ₂),(2, r ₀ r ₁ r ₂),(2, a ₂ r ₀ r ₁ r ₂),

(1, a ₂ r ₀ r ₁ r ₂),(1, a ₁ a ₂ r ₀ r ₁ r ₂),(0, a ₁ a ₂ r ₀ r ₁ r ₂),(0, a ₀ a ₁ a ₂ r ₀ r ₁ r ₂) = (0, g )},

{(0,1),(0, a ₀),(2, a ₀),(0, r ₂ a ₀),(1, r ₂ a ₀),(2, r ₁ r ₂ a ₀),(0, r ₁ r ₂ a ₀),(1, r ₀ r ₁ r ₂ a ₀),(2, r ₀ r ₁ r ₂ a ₀),

(2, a ₂ r ₀ r ₁ r ₂ a ₀),(1, a ₂ r ₀ r ₁ r ₂ a ₀),(1, a ₁ a ₂ r ₀ r ₁ r ₂ a ₀),(0, a ₁ a ₂ r ₀ r ₁ r ₂ a ₀) = (0, g )},

{(0,1),(1, a ),(0, a ),(0, a a ),(2, a a ),(0,r a a ),(1,r a a ),(2,r r a a ),(0,rr a a ), (1,r0r1r2a0a1),(2,r0r1r2a0a1),(2,a2r0r1r2a0a1),(0,a2r0r1r2a0a1)= (0,g)} and so on. Therefore, we obtain that G is generated by A ∪ A ∪ A ∪ R ∪ R ∪ R .

Let X = TCay( G ; A , A , A ; R , R , R ) be a connected tri-Cayley graph over a group G . According to the definition of tri-Cayley graph and Lemma 3.4, we will construct two classes of 4-valent tri-Cayley graphs over cyclic group G = Z = 〈 b 〉 . As shown below:

X 1 = TCay( G ; ∅ , ∅ , ∅ ;{1, b },{1, b },{1, b }); (7)

X 2 = TCay( G ;{ b , b ^- ¹},{ b , b ^- ¹},{ b , b ^- ¹};{1},{1},{1}). (8)

4. X₁=TCay(G; 0 , 0 , 0 ;{1,b},{1,b},{1,b})

Theorem 4.1 Let X = TCay( G ; 0 , 0 , 0 ;{1, b },{1, b },{1, b}) be a connected 4-valent 0-type tri-Cayley over a group G . Then X is vertex-transitive.

Proof: For any b e G , we define y ^: V ( X ) ^ V ( X ) by

γ :(0, bⁱ ) (1, bⁱ ), (1, bⁱ ) (2, bⁱ ), (2, bⁱ ) (0, bⁱ ) , (9)

where i = 0,1, ,10 . It is easy to see that γ is a bijection. Next, we claim that γ ∈ Aut( X ) . We have

N ((0, bⁱ )) ^γ = {(1, bⁱ ),(1, bⁱ ⁺ ¹),(2, bⁱ ),(2, bⁱ ^- ¹)} ^γ = {(2, bⁱ ),(2, bⁱ ⁺ ¹),(0, bⁱ ),(0, bⁱ ^- ¹)} = N ((1, bⁱ )),

N ((1, bⁱ )) ^γ = {(2, bⁱ ),(2, bⁱ ⁺ ¹),(0, bⁱ ),(0, bⁱ ^- ¹)} ^γ = {(0, bⁱ ),(0, bⁱ ⁺ ¹),(1, bⁱ ),(1, bⁱ ^- ¹)} = N ((2, bⁱ )),

N ((2, bⁱ )) ^γ = {(0, bⁱ ),(0, bⁱ ⁺ ¹),(1, bⁱ ),(1, bⁱ ^- ¹)} ^γ = {(1, bⁱ ),(1, bⁱ ⁺ ¹),(2, bⁱ ),(2, bⁱ ^- ¹)} = N ((0, bⁱ )).

Therefore, γ ∈ Aut( X ) and so 〈 R ( G ), γ 〉 acts transitively on V ( X ). Then X is vertex-transitive.

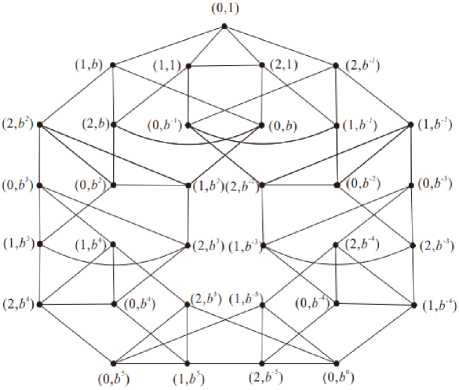
Fig 1. The tri-Cayley graph X = TCay( G ; ∅ , ∅ , ∅ ;{1, b },{1, b },{1, b }) .

Theorem 4.2 Let X = TCay( G ; ∅ , ∅ , ∅ ;{1, b },{1, b },{1, b }) be a connected 4-valent 0-type tri-Cayley over a group G . Then Aut( X ) = 〈 R ( G ), γ 〉 Z , where γ is defined in Theorem 4.1.

Proof: By Lemma 3.2, we can get that

| A | = | A (0,1) ||(0,1) ^A | = | A (0,1)(1,1) ||(1,1) ^A ^(0,1) ||(0,1) ^A | = | A (0,1)(1,1)(2,1) ||(2,1) ^A ^(0,1)(1,1) ||(1,1) ^A ^(0,1) ||(0,1) ^A |, (13)

where A = Aut( X ) . By Theorem 4.1, we know that X is vertex-transitive, one has | (0,1) ^A | = 33 . Next, we will get | A | in three steps.

^{(i) |} ^A (0,1)(1,1)(2,1) ^| ⁼ ^1.

We know that vertices (0,1) , (1,1) and (2,1) are fixed and N ((0,1)) = {(1,1), (1, b ), (2, b ^- ¹), (2,1)} . Suppose there exists η ∈ A shch that (1, b ) ^η = (2, b ^- ¹) . By Figure 1, we can get that

| N ((2, b ²)) ∩ N ((0,1))| = | N ((1, b ^- ²)) ∩ N ((0,1))| = 1 (14)

and

| N ((2, b )) ∩ N ((0,1))| = | N ((0, b ^- ¹)) ∩ N ((0,1))| = | N ((0, b )) ∩ N ((0,1))| = | N ((1, b ^- ¹)) ∩ N ((0,1))| = 2. (15)

We know that vertices (1,1) and (2,1) are fixed, one has (2, b ²) ^η = (1, b ^- ²) , (2, b ) ^η = (0, b ^- ¹) and (0, b ) ^η = (1, b ^- ¹) . Applying the connection relationship of edges, we have the following result. For N ((0,1)) , we have (0, b ³) ^η = (0, b ^- ³) , (0, b ²) ^η = (2, b ^- ²) and (1, b ²) ^η = (0, b ^- ²) ; for N ((0,1)) , we have (1, b ³) ^η = (1, b ^- ³) , (1, b ⁴) ^η = (2, b ^- ⁴) and (2, b ³) ^η = (2, b ^- ³) ; for N ((0,1)) , we have (2, b ⁴) ^η = (0, b ^- ⁴) , (0, b ⁴) ^η = (1, b ^- ⁴) and (2, b ⁵) ^η = (1, b ^- ⁵) ; for N ((0,1)) , we have (0, b ⁵) ^η = (2, b ^- ⁵) and (1, b ⁵) ^η = (0, b ⁶). However,

| N ((0, b ⁵)) ∩ N 5 ((0,1))| = 3 ≠ | N ((2, b ^- ⁵)) ∩ N 5 ((0,1))| = 2 (16)

and

|N((1,b5))∩N5((0,1))|=2≠|N((0,b6))∩N5((0,1))|=3,(17)

a contradiction. Therefore, | A|

(ii) | (2,1)A(0,1)(1,1)

We know that vertices (0,1) and (1,1) are fixed and N ((0,1)) = {(1,1), (1, b ), (2, b ^- ¹), (2,1)} . By Figure 1, we can get that [(0,1),(1,1),(2,1)] is the unique 3-cycle passing through the vertex (2,1). Thus there is no a graph automorphism which causes the vertex (2,1) to become the vertex (1, b ) or (2, b ^- ¹) and fixes vertices (0,1) and (1,1) . Then the vertex (2,1) is fixed. Therefore, | (2,1) ^A ^(0,1)(1,1) | = 1 .

(iii) | (1,1) ^A ^(0,1) | = 2 .

We know that the vertex (0,1) is fixed and N ((0,1)) = {(1,1), (1, b ), (2, b ^- ¹), (2,1)} . By Figure 1, we can get that [(0,1),(1,1),(2,1)] is the unique 3-cycle passing through the vertex (1,1). Thus there is no a graph automorphism which causes the vertex (1,1) to become the vertex (1, b ) or (2, b ^- ¹) and fixes the vertex (0,1) . For any b ∈ G , we define δ : V ( X 1 ) V ( X 1 ) by

δ:(0,bi) (0,b-i), (1,bi) (2,b-i), (2,bi) (1,b-i),(18)

where i = 0,1, ,10 . It is easy to see that δ is a bijection. Next, we claim that δ ∈ Aut( X ) . We have

N((0,bi))δ={(1,bi),(1,bi+1),(2,bi),(2,bi-1)}δ={(2,b-i),(2,b-i-1),(1,b-i),(1,b-i+1)}=N((0,b-i)),(19)

N((1,bi))δ={(2,bi),(2,bi+1),(0,bi),(0,bi-1)}δ={(1,b-i),(1,b-i-1),(0,b-i),(0,b-i+1)}=N((2,b-i)),(20)

N((2,bi))δ={(0,bi),(0,bi+1),(1,bi),(1,bi-1)}δ={(0,b-i),(0,b-i-1),(2,b-i),(2,b-i+1)}=N((1,b-i)).(21)

Therefore, δ ∈ Aut( X ) . Since o ( δ ) = 2 and (0,1) ^δ = (0,1) , then (1,1) ^A ^(0,1) ≅ Z . Therefore, | (1,1) ^A ^(0,1) | = 2 .

Consequently, Aut( X ) = 〈 R ( G ), γ 〉 Z , where γ is defined in Theorem 4.1.

Theorem 4.3 Let X = TCay( G ; ∅ , ∅ , ∅ ;{1, b },{1, b },{1, b }) be a connected 4-valent 0-type tri-Cayley over a group G . Then X is not edge-transitive.

Proof: By Figure 1, we can get that there exists a 3-cycle [(0,1),(1,1),(2,1)] passing through the edge {(0,1),(1,1)} but not passing through the edge {(0,1),(1, b )}. Therefore, X is not edge-transitive.

Theorem 4.4 Let X = TCay( G ; ∅ , ∅ , ∅ ;{1, b },{1, b },{1, b }) be a connected 4-valent 0-type tri-Cayley over a group G . Then X is not arc-transitive.

Proof: By Theorem 4.1 and Theorem 4.3, we can get that X is not arc-transitive.

5. X 2 = TCay(G;{b,b^-1},{b,b^-1},{b,b^-1};{1},{1},{1})

Theorem 5.1 Let X = TCay( G ;{ b , b ^- ¹},{ b , b ^- ¹},{ b , b ^- ¹};{1},{1},{1}) be a connected 4-valent 2-type tri-Cayley over a group G . Then X is vertex-transitive.

Proof: For any b ∈ G , we define φ : V ( X ) V ( X ) by

φ :(0, bⁱ ) (1, b ^- ⁱ ) , (1, bⁱ ) (2, b ^- ⁱ ) , (2, bⁱ ) (0, b ^- ⁱ ), (22)

where i = 0,1, ,10 . It is easy to see that φ is a bijection. Next, we claim that φ ∈ Aut( X ) . We have

N ((0, bⁱ )) ^φ = {(1, bⁱ ),(2, bⁱ ),(0, bⁱ ⁺ ¹),(0, bⁱ ^- ¹)} ^φ = {(2, b ^- ⁱ ),(0, b ^- ⁱ ),(1, b ^- ⁱ ^- ¹),(1, b ^- ⁱ ⁺ ¹)} = N ((1, b ^- ⁱ )), (23)

N ((1, bⁱ )) ^φ = {(2, bⁱ ),(0, bⁱ ),(1, bⁱ ⁺ ¹),(1, bⁱ ^- ¹)} ^φ = {(0, b ^- ⁱ ),(1, b ^- ⁱ ),(2, b ^- ⁱ ^- ¹),(2, b ^- ⁱ ⁺ ¹)} = N ((2, b ^- ⁱ )), (24)

N ((2, bⁱ )) ^φ = {(0, bⁱ ),(1, bⁱ ),(2, bⁱ ⁺ ¹),(2, bⁱ ^- ¹)} ^φ = {(1, b ^- ⁱ ),(2, b ^- ⁱ ),(0, b ^- ⁱ ^- ¹),(0, b ^- ⁱ ⁺ ¹)} = N ((0, b ^- ⁱ )). (25)

Therefore, φ ∈ Aut( X ) and so 〈 R ( G ), φ 〉 acts transitively on V ( X ). Then X is vertex-transitive.

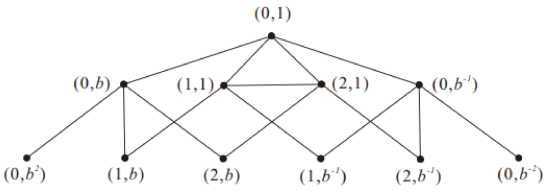
Fig.2. The induced subgraph of X = TCay( G ;{ b , b ^- ¹},{ b , b ^- ¹},{ b , b ^- ¹};{1},{1},{1}) .

Theorem 5.2 Let X = TCay( G ;{ b , b ^- ¹},{ b , b ^- ¹},{ b , b ^- ¹};{1},{1},{1}) be a connected 4-valent 2-type tri-Cayley over a group G . Then Aut( X ) = 〈 R ( G ), φ 〉 Z , where φ is defined in Theorem 5.1.

Proof: By Lemma 3.2, we can get that

| A | = | A (0,1) ||(0,1) ^A | = | A (0,1)(1,1) ||(1,1) ^A ^(0,1) ||(0,1) ^A | = | A (0,1)(1,1)(2,1) ||(2,1) ^A ^(0,1)(1,1) ||(1,1) ^A ^(0,1) ||(0,1) ^A |, (26)

where A = Aut( X ) . By Theorem 5.1, we know that X is vertex-transitive, one has | (0,1) ^A | = 33 . Next, we will get | A | in three steps.

(i) | A (0,1)(1,1)(2,1) | = 2 .

For any b ∈ G , we define ρ : V ( X ) V ( X ) by

ρ:(0,bi) (0,b-i) , (1,bi) (1,b-i) , (2,bi) (2,b-i),(27)

where i = 0,1, ,10 . It is easy to see that ρ is a bijection. Next, we claim that ρ ∈ Aut( X ) . We have

N((0,bi))ρ={(1,bi),(2,bi),(0,bi+1),(0,bi-1)}ρ={(1,b-i),(2,b-i),(0,b-i-1),(0,b-i+1)}=N((0,b-i)),(28)

N((1,bi))ρ={(2,bi),(0,bi),(1,bi+1),(1,bi-1)}ρ= {(2,b-i),(0,b-i),(1,b-i-1),(1,b-i+1)}=N((1,b-i)),(29)

N((2,bi))ρ={(0,bi),(1,bi),(2,bi+1),(2,bi-1)}ρ={(0,b-i),(1,b-i),(2,b-i-1),(2,b-i+1)}=N((2,b-i)).(30)

Therefore, ρ ∈ Aut( X ). Since o ( ρ ) = 2, (0,1) ^ρ = (0,1), (1,1) ^ρ = (1,1) and (2,1) ^ρ = (2,1) , then A ≅ Z . ^{Therefore, |} ^A (0,1)(1,1)(2,1) ^| ⁼ ^2.

(ii) | (2,1) ^A ^(0,1)(1,1) | = 1.

We know that vertices (0,1) and (1,1) are fixed and N ((0,1)) = {(1,1), (2,1), (0, b ), (0, b ^- ¹)} . By Figure 2, we can get that [(0,1),(1,1),(2,1)] is the unique 3-cycle passing through the vertex (2,1). Thus there is no a graph automorphism which causes the vertex (2,1) to become the vertex (0, b ) or (0, b ^- ¹) and fixes vertices (0,1) and (1,1) . Then the vertex (2,1) is fixed. Therefore, | (2,1) ^A ^(0,1)(1,1) | = 1 .

(iii) | (1,1) ^A ^(0,1) | = 2 .

We know that the vertex (0,1) is fixed and N((0,1)) = {(1,1), (2,1), (0, b), (0, b-1)} . By Figure 2, we can get that [(0,1),(1,1),(2,1)] is the unique 3-cycle passing through the vertex (1,1). Thus there is no a graph automorphism which causes the vertex (1,1) to become the vertex (0, b) or (0, b-1) and fixes the vertex (0,1) . For any b∈ G, we define θ:V(X2) V(X2)by

θ:(0,bi) (0,b-i) , (1,bi) (2,b-i) , (2,bi) (1,b-i) ,(31)

where i = 0,1, ,10 . It is easy to see that θ is a bijection. Next, we claim that θ ∈ Aut( X ) . We have

N((0,bi))θ={(1,bi),(2,bi),(0,bi+1),(0,bi-1)}θ= {(2,b-i),(1,b-i),(0,b-i-1),(0,b-i+1)}=N((0,b-i)),(32)

N((1,bi))θ={(2,bi),(0,bi),(1,bi+1),(1,bi-1)}θ={(1,b-i),(0,b-i),(2,b-i-1),(2,b-i+1)}=N((2,b-i)) ,(33)

N((2,bi))θ={(0,bi),(1,bi),(2,bi+1),(2,bi-1)}θ={(0,b-i),(2,b-i),(1,b-i-1),(1,b-i+1)}=N((1,b-i)) .(34)

Therefore, θ ∈ Aut( X ) . Since o ( θ ) = 2 and (0,1) ^θ = (0,1) , then (1,1) ^A ^(0,1) ≅ Z . Therefore, | (1,1) ^A ^(0,1) | = 2 .

Consequently, Aut( X ) = 〈 R ( G ), φ 〉 Z , where φ is defined in Theorem 5.1.

Theorem 5.3 Let X = TCay( G ;{ b , b ^- ¹},{ b , b ^- ¹},{ b , b ^- ¹};{1},{1},{1}) be a connected 4-valent 2-type tri-Cayley over a group G . Then X is not edge-transitive.

Proof: By Figure 2, we can get that there exists a 3-cycle [(0,1),(1,1),(2,1)] passing through the edge {(0,1),(1,1)} but not passing through the edge {(0,1), (0, b )} . Therefore, X is not edge-transitive.

Theorem 5.4 Let X = TCay( G ;{ b , b ^- ¹},{ b , b ^- ¹},{ b , b ^- ¹};{1},{1},{1}) be a connected 4-valent 2-type tri-Cayley over a group G . Then X is not arc-transitive.

Proof: By Theorem 5.1 and Theorem 5.3, we can get that X is not arc-transitive.

6. Conclusions

We know that it is very difficult to classify 4-valent tri-Cayley graphs over cyclic group. In this paper, we construct two classes of 4-valent tri-Cayley graphs over cyclic group. Meantime, the automorphism groups of two classes of 4-valent tri-Cayley graphs over cyclic group are discussed. In addition, the vertex transitivity, edge transitivity and arc transitivity are proved. The method in this article has reference value. In later work, we can use this idea to classify 4-valent tri-Cayley graphs over other group.

Acknowledgments

This work is supported by National Natural Science Foundation of China (grant numbers 12126317 and 11501172).

Список литературы The Construction of two classes of 4-valent tri- Cayley Graphs over Cyclic Group

J. A. Bondy, U. S. R. Murty, Graph Theory with Applications, Elsevier North Holland, New York, 1976.
H. Wielandt, Finite Permutation Groups, Academic Press, New York, 1964.
K. Kutnar, D. Marušič, S. Miklavič, P. Šparl, Strongly regular tri-Cayley graphs, European Journal of Combinatorics. (2009), 30(4), 822-832.
I. Koács, K. Kutnar, D. Marušič, S. Wilson, Classification of cubic symmetric tricirculants, The Electronic Journal of Combinatorics. (2012), 19(2), 24.
P. Potočnik, M. Toledo, Classification of cubic vertex-transitive tricirculants, arXiv preprint arXiv: 1812.04153, 2018.
D. Marušič, T. Pisanski, Symmetries of hexagonal molecular graphs on the torus, Croatica Chemica Acta. (2000), 73(4), 969-981.
M. Boben, T. Pisanski, A. Žitnik, I‐graphs and the corresponding configurations, Journal of Combinatorial Designs. (2005), 13(6), 406-424.
A. Devillers, M. Giudici, W. Jin, Arc-transitive bicirculants, Journal of the London Mathematical Society. (2022), 105(1), 1-23.
W. Jin, Two-arc-transitive bicirculants, arXiv preprint arXiv: 2211.14520, 2022.
I. Koács, B. Kuzman, A. Malnič, S. Wilson, Characterzation of edge-transitive 4-valent bicirculant, Journal of Graph Theory. (2012), 69, 441-463.
T. Pisanski, A classification of cubic bicirculants, Discrete Mathematics. (2007), 307(3-5), 567-578.
I. Kovács, A. Malnič, D. Marušič, Š. Miklavič, One-matching bi-Cayley graphs over abelian groups, European Journal of Combinatorics. (2009), 30(2), 602-616.
J. X. Zhou, Y. Q. Feng, Cubic bi-Cayley graphs over abelian groups, European Journal of Combinatorics. (2014), 36, 679-693.
M. Conder, J. X. Zhou, Y. Q. Feng, M. M. Zhang, Edge-transitive bi-Cayley graphs, Journal of Combinatorial Theory, Series B. (2020), 145, 264-306.
J. M. Pan, Y. N. Zhang, An explicit characterization of cubic symmetric bi-Cayley graphs on nonabelian simple groups, Discrete Mathematics. (2022), 345(9): 112954.
M. M. Zhang, J. X. Zhou, Trivalent vertex-transitive bi-dihedrants, Discrete Mathematics. (2017), 340(8), 1757-1772.
M. Y. Xu, Finite group preliminary, Science Press, Bei Jing, 2014.

Еще

Статья научная