The deformability of polycarbonate / poly (ethylene terephthalate) blends

DOI:

Polymer blends represent great practical interest, since they allow to obtain novel polymeric materials, not restorting new polymers synthesis. Polycarbonate (PC) and poly(ethylene terephthalate) are used during many years as engineering materials, having many useful properties. PC/PET blends are of great interest and consequently a large amount of their miscibility structure and properties has been fulfilled [6-8; 16]. It was found out [16], that the blends PC/PET with PC large content had two glass transition temperatures, whereas blends rich in PET exhibited only one. Hence, these blends are only partly miscible. The most interesting feature of these blends mechanical behaviour is their deformability maximum within the range of 60-80 mass. % PET. The authors [16] have pointed out that physical fundamentals of this effect are unclear. Therefore the purpose of the present work is the study of this important from practical point of view effect with fractal analysis notions usage.

Experimental

Polycarbonates were used o n the basis of bisphenol A of Lexan 131-111 ( M _n = 13.300 and M _w = 34.200) provided by General Electric Co. and the poly(ethylene terephthalate) was a bottle grade material (intrinsic viscosity = 0.74 dl/g), supplied by Celanese Plastics and Specialties Co., with the commercial designation Petpac 2113 [16].

Pellets of PC and PET were combined in the desired weight ratio and then dried for 1214 hours in an air oven at 353 K to remove sorbed water. Further the dried pellets were heated to 408 K to promote crystallization of PET and blended in melt with the usage of screw extruder, having screw diameter of 19 mm and screw length/diameter ratio of 20. The extrudate was quenched by passing it through an ice water bath and was chopped into pellets. Then the blends pellets were subjected to injection molding by a ram type machine to form ASTM D-638 dog-bone specimens for mechanical testing. The tension testing was fulfilled on testing machine of Type T5002 of firm Lloyd Instrument Ltd. production at temperature of 293 K and a cross head speed of 50 mm/min [16].

Results and Discussion

As it is known [14], the most general informator about solids structure is its fractal dimension d _f , which can be calculated according to the equation [1]:

d f = ( d - 1)(1 + V), (1)

where d is the dimension of Euclidean space, in which a fractal is considered (it is obvious, that in our case d = 3), n is Poisson’s ratio, which is determined by the mechanical tests results with the aid of the relationship [10]:

о Y _ 1 - 2v E " 6(1 + v) ’

where s _Y and E are yield stress and elastic modulus of polymeric materials, respectively.

Within the frameworks of fractal analysis limiting strain at break ε ^l _f ^im is determined theoretically as follows [11]:

In Fig. 2 the dependence of e _f on fractal dimension d _f for blends PC/PET is adduced. As one can see, good enough linear correlation e _f ( d _f ) is obtained, which can be approximated by the following empirical equation:

lim _ DcD - 1 - 1

^£ f = ^C ”

where C „ is characteristic ratio, which is an indicator of polymer chain statistical flexibility [5], D_ch is fractal dimension of a chain part between its fixation point, characterizing molecular mobility level [12].

C „ value is connected with dimension d f by the following relationship [12]:

2 d

C„ =------- f -----+ -,

” d ( d - 1)( d - d_f ) 3

and the simplest method of dimension D _ch estimation is the empirical formula [12]:

£ f = -25( d_f - 2.25), %.            (6)

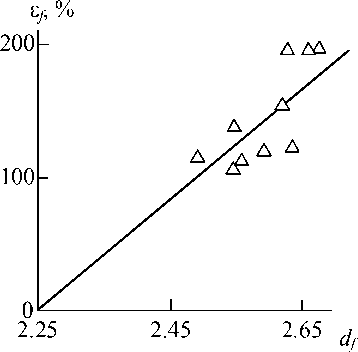
Fig. 2. The dependence of strain at break e _f on structure fractal dimension d_f for blends PC/PET

D _ch = 2.1 d _f - 3.8 .               (5)

In Fig. 1 the comparison of the obtained experimentally and calculated according to the equation (3) dependences of strain at break e _f on PET content C _PET in blends PC/PET is adduced. As one can see, well enough both qualitative and quantitative (the average discrepancy of theory and experiment makes up ~15 %) correspondence of the indicated dependences is obtained.

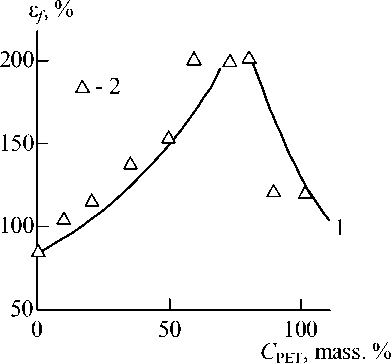
Fig. 1. The calculated according to the equation ( 3 ) ( 1 ) and obtained experimentally ( 2 ) dependences of strain at break e on PET content C in blends ^f PC/PET ^PET

The equation (6) allows to estimate limiting maximum e _f magnitude for the considered blends PC/PET. As it is known [1], the greatest value d _f for real solids is equal to 2.95 and in this case maximum value e _f is equal to ~298 %. The linear dependence e _f ( d _f ) extrapolation to e _f = 0 at d _f = 2.25 is also of interest, the causes of which will be considered below.

There exists a number of specific effects, which should be taken into consideration at their study: components interaction, level of autohesion between them and so on. Interaction between components of the considered blends, i.e. PC and PET, can be described with the aid of Flory-Huggins interaction parameter c _AB [13], which is defined within the framework of fractal analysis with the aid of the equation [9]:

D f = 1.50 + 0.-5x ab (7)

where D_f is dimension of macromolecular coil, which is estimated for linear polymers according to the formula [9]:

Id,

D f = -3 f .                 (8)

In Fig. 3 the dependence of ef on Flory-Huggins interaction parameter cAB is adduced, which is approximated well enough by linear correlation and is described analytically by the following empirical equation:

For the considered PC/PET blends D^a_f^v = 1.73 and then the equation (10) can be written as follows:

e f = 275x ab , % .                (9)

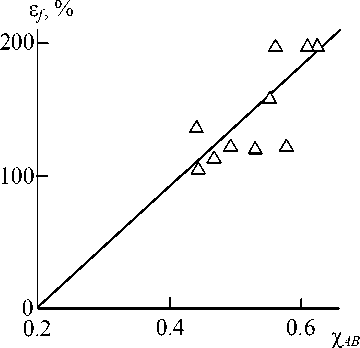
Fig. 3. The dependence of strain at break e _f on Flory-Huggins interaction parameter c _AB for blends PC/PET

At the greatest value D _f = 1.967 according to the equation (8) at d _f = 2.95 the value c _AB = 1.038 and the greatest value e _f = 285 %, that corresponds well enough to the cited above similar value e _f , which was estimated according to the formula (6).

The level of autohesion between PC/PET blend components can be estimated with the aid of shear strength of autohesional bonding t _c , which is given within the frameworks of generalized fractal model as follows [15]:

1пт _c = R 22 ^{D f —} 3 — 8-218. (13)

The obtained according to the equation (13) values t _c vary within the limits of 0.00510.0217 MPa, that corresponds to shear strength of autohesional bonding of other polymer pairs [4]. In Fig. 4 the dependence e _f (τ¹ _c ^/2) is adduced (such form of the indicated dependence is chosen with the purpose of its linearization) for the considered blends, which has shown e _f growth at t _c increasing, that can be expressed analytically as follows:

e _f = 417<^/2, %-             (14)

Let us note, that the dependence e _f (τ¹ _c ^/2) is extrapolated to e _f = 0, i.e. absolutely brittle solid, at t _c = 0. This means, that availability of finite nonzero strength of autohesional bonding between blend components is the necessary condition of their nonzero deformability.

ln^T c = ⁽ N c ^— c ) - 4-4,            ⁽¹⁰⁾

where N_c is intersections (contacts) of macromolecular coils number in boundary layer of autohesional bonding, c is constant, which is defined according to the equation [15]:

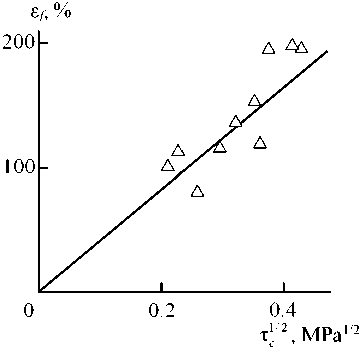
Fig. 4. The dependence of strain at break e _f on shear strength of components autohesional bonding t _c for blends PC/PET.

Let us return to the plot of Fig. 2, which gives zero value e _f at d_f = 2.25. As it follows from the equation (8), the indicated value d_f corresponds to the dimension of permeable (transparent) macromolecular coils of D_f = 1.50 [2], i.e. such coils, which can pass freely through one another. This effect reflects the relationship (12) – at D_f £ 1 .50 the exponent at R_g becomes a negative one, that results to N_c sharp reduction and according to the equation (13) – to corresponding reduction of shear strength t _c of autohesional bonding PC-PET.

c = 16.6( D a - 1-50),

where D ^a _f ^v is average fractal dimension of macromolecular coils.

The value N _c can be calculated (in relative units) according to the following relationship [19]:

2 D — d N c ~ R _g f ,

where R_g is gyration radius of macromolecular coil, which further at the first approximation is accepted equal to 15 nm.

Conclusions

Thus, the present work results have shown that the extreme enhancement of the strain at break for PC/PET blends is due to corresponding structural changes of the indicated blends, which are characterized by their structure fractal dimension variation. The blends deformability rise can be achieved by the enhancement of either Flory-Huggins interaction parameter, or shear strength of their autohesional contact. The transparence threshold of macromolecular coil achievement results in sharp reduction of strain at break, i.e. its decrease practically up to zero value.

Acknowledgements

The work is performed within the complex project on creation of hi-tech production with the participation of the Russian higher educational institution, the Contract of Tanneta JSC with the Ministry of Education and Science of the Russian Federation of February 12, 2013 No. 02.G25.31.0008 (Resolution of the Government of the Russian Federation No. 218).