The dependence analysis of durability, the catastrophe risk and the transport effectiveness on the airplane construction mass

One of the main perfection characteristics of the civil aviation airplanes is ratio between the construction mass to the quantity of passenger seats, i. e. the airplane construction mass per a passenger seat. The lower this index is, the higher the airplane economic effectiveness will be. From the other hand, decreasing the construction mass is connected with decreasing its durability and increasing the catastrophe risk. In the work the attempt to analyse the conditions and restrictions within the limits of minimizing aircraft deadload is done.

The maximal take off mass of the airplane M _max may consist of: the payload mass M _П.Г (passengers and cargos), the fuel mass M_Т and the airplane construction mass M _К . For example, for the airplane Tu-204, the flying mass components are:

M max = 107,9T;

M _П.Г = 25,2 T;

M_Т = 32,7 T;

M = 50 T.

К

When M_Т and M _max are fixed, the change is possible only due to construction mass and the payload mass.

Aircraft construction durability the ability to resist the flight loads without destruction are defined by the section area of its power elements. When the construction materials are non-changeable, the durability is directly proportional to the construction mass. The durability defines the destruction risk or the catastrophe risk and it is exactly connected with payload mass. For Tu-204 airplane the connection is defined as:

M П.Г = M max - M t - M k = 75,2 - M k .

The task is to specify the influence of construction mass on its destruction probability, i. e. catastrophe realization.

Tu-204 airplane mass is 50 t. It is defined due to the condition of its ability to resist the double overload n without destruction under the maximal mass with the structural load factor k = 1.5. And the probability of destruction, due to NFC, must be <  1 ■ 10 ^{- 9} [1].

If the airplane construction mass Mmax is divided into the overload value n = 2 and the safe load factor is k = 1.5, then under MК = 16.6 t the airplane with maximal take off mass will be destructed with probability Q = 1.

The viewed conditions define the two points of destruction functional dependence Q = f ( M k ) of construction mass. It is absolutely obvious, that when M_k f 50 t , then the probability of destruction exists, although it becomes less then 1 ■ 10 ^{- 9} . We can predict, that the probability of destruction will asymptotically tend to zero while the construction mass increasing. This prediction may be realized if the exponential dependence equals to Q = f ( M k ).

Then, according to the earlier highlighted conditions, we can reveal Tu-204 aircraft construction destruction probability:

Q = exp0.6138(16.6 - M k ).

Due to that formula the calculations of construction mass destruction probabilities and payload masses are calculated. They are shown in the tab. 1.

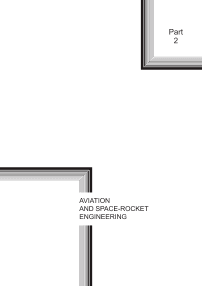
It is very difficult to build the graphic dependences Q = f ( M k ) in its changeable range from 1 to 5.82 ■Ю ^{- 15} . That is why the dependence LnQ = f ( M _ПГ) is shown in

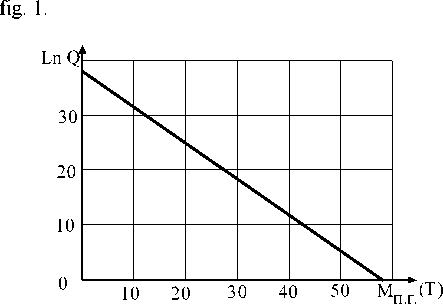
Fig. 1. Dependence of the airplane destruction probability of useful load mass

Tab. 1 and fig. 1 show us that in the range the construction mass is increasing, the probability of construction destruction is continuously decreasing. In order to have the graphic representation of the curve character Q = f ( M k ) there is a view of that line at the beginning and ending parts of M_k changing range in fig. 2 and 3.

Construction masses, useful load masses and airplane destruction probabilities

Table 1

М k , т	16,6	20	30	40	50	60	70
M п.г , т	58.6	55.2	45.2	35.2	25.2	15.2	5.2
Q	1	0.124	2.6 ⋅ 10–4	5.78 ⋅ 10–7	1 ⋅ 10–9	2.7 ⋅ 10–12	5.82 ⋅ 10–15

The presented pictures demonstrate that the meaning of rated construction destruction probability 1 ⋅ 10 ^{- 9} is neither peculiar nor characteristic point on the line Q = f ( M_k ). There is a question how could we make the border meaning of catastrophic situation probability 1 ⋅ 10 ^{- 9} ? The answer is in paragraph 2.4 of ICAO continuing airworthiness manual [2]. It is said that: “…2.4. To estimate the design acceptability, it was necessary to specify the well-grounded probability meanings defined due to the next basement:

a) the exploitation experience claims that serious aviation event due to the exploitative and constructive character, may appear approximately one time per one million hours of flight. In 10 % of events it may be connected with breakdown conditions appearing due to aircraft systems breakdown. It was thought that for new constructions the probability of serious aviation events (that were summoned by the system breakdown) must not exceed that index. That is why it is necessary the probability of a serious aviation event happening due to the breakdown conditions does not exceed one event per 10 million hours of flight, so the probability must be less than10–7;

b) in order to be sure that index is realised, it is necessary to complete the complex quantitative analysis of the airplane’s systems work reliability. The random assumption was made about approximately 100 potential breakdown conditions, which could prevent the continuing safe flight and landing. The predetermined probability of an event, which was 10 ^{- 7} distributed uniformly among those conditions, finally the probability of each breakdown condition not more than 1 ⋅ 10 ^{- 9} was stipulated. So, the upper limit of probability of one breakdown condition, which will not allow continuing the flight safely and completing the landing, is based on the level of 1 ⋅ 10 ^{- 9} for each flight hour…”

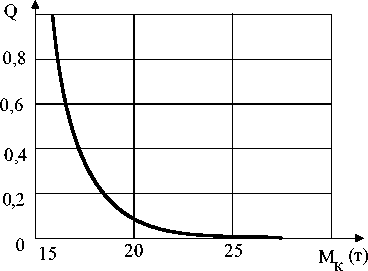
Fig. 2. Dependence of probability during lesser masses

This limit is undoubtedly defined for such breakdown condition, which is stipulated by insufficient reliability and durability of the airplane construction and each of its systems. It is obvious, that there are some essential uncertainties in determination of standard value for probability of catastrophic event 1⋅10-9 .

Fig. 3. Dependence of probability of construction destruction in range of the calculated mass

So in paragraph 2.4, a definition of serious aviation event frequency is less than 1 ⋅ 10 ^{- 7} . It contains two suppositional estimations changing during the period of exploitation.

In paragraph 2.4, b the random assumption about 100 potential breakdown conditions, which guide to a catastrophe, was adopted. Finally, the upper boarder of catastrophic events probability was got caused by the breakdowns of aviation technique, that is 1 ⋅ 10 ^{- 9} per a flight hour. This estimation is perceived as generalized estimation of airplane constructing experience. It is obvious, careful obtaining of such estimation by the theoretical and experimental materials is impossible.

Airplane developers have to prove the inadmissibility of the catastrophic breakdown conditions with probability not more than 1 ⋅ 10 ^{- 9} in evidential documentation, which confirms that an airplane meets the demands of NFC. It is also a very difficult task.

There are estimations of attitude of the airplane construction mass to the maximal take off mass in the tab. 2 and 3. The average meaning of relative construction mass for short range airplanes is 0,586, for the medium range aircraft – 0.542, and for the long haul – 0.472. That divergence for airplanes of different classes is quite explainable.

The short range airplanes have the nonstop flight duration of 1–2 hours, and the long haul – 10–12 hours of flight. Having the same resource of 60 thousands of flight hours, the short range airplanes experience 5 times more load cycles, defined by take offs and landings, in comparison with long hauls. The diversity of relative masses for the same type of aircrafts is in limits of 11–12 %, it is very essential and hard to explain.

Judging by data of the table 1 and fig. 3 it is clear that, for examined Tu-204 aircraft, the decreasing destruction probability from meaning of 5.78⋅10-7 up to 1⋅10-9 for 1 hour demands to increase the mass of construction payload from 40 to 50 t, that in practice will guide to decreasing payload mass from 35.2 to 25.2 t. The reliability of airplane within destruction probability meanings of 1⋅10-9 for 1 hour is hard to predict and prove, and its increasing is connected with valuable decreasing payload mass and commercial outcome – the competitive ability. The reliability increasing and decreasing the catastrophe damage, in this case, is connected with increasing the transport cost.

According to this 11–12 % of one class airplane construction diversity, under the same level of machine building production may be reckoned among various risk levels of the developers of airplanes, because decreasing the airplane’s construction mass by 10 % increases the destruction risk from 1 ⋅ 10 ^{- 9} up to 5 ⋅ 10 ^{- 8} .