The development and investigation of the efficiency of the differential evolution algorithm for solving multi-objective optimization problems
Автор: Erokhin D. A., Akhmedova Sh. A.
Журнал: Siberian Aerospace Journal @vestnik-sibsau-en
Рубрика: Informatics, computer technology and management
Статья в выпуске: 2 vol.20, 2019 года.
Бесплатный доступ
In practice problems, which consist in the search of the best (optimal) solution according to the different irredundant and contradictory (conflicting) criteria, called multi-objective problems, are of frequent occurrence. One of the most commonly used methods for solving this kind of problems consists in combination of all criteria into the single one by using some linear relation. However, despite the simplicity of this method, solving problems with its help may cause other problems related to the determination of the mentioned linear combination, namely related to the determination of the weight coefficients for each criterion. The incorrect selection of these coefficients may lead to non-optimal solutions (according to the Pareto theory). In this regard, recently various population-based algorithms have been proposed for solving the described problems, which are the modifications of these population-based algorithms for solving singleobjective optimization problems. This article describes the developed modifications of the Differential Evolution algorithm (DE) for solving multi-objective unconstrained optimization problems based on the well-known NSGA (Nondominated Sorting Genetic Algorithm) and MOEA/D (Multiobjective Evolutionary Algorithm Based on Decomposition) schemes, which use the Pareto theory. The investigation into the efficiency of the Differential Evolution algorithm for solving multi-objective optimization problems in relation to the chosen mutation operator of the original DE algorithm and to the multi-objective scheme was conducted. The developed modifications were tested by using some well-known multi-objective real-valued optimization problems with 30 variables, such as ZDT1, ZDT2, ZDT3, etc. The practical problem of spacecraft control contour variant choice was solved as well. The experimental results show that better results were achieved by the Differential Evolution algorithm with the simplest mutation operators combined with the NSGA scheme. Thus, the applicability of the described modification for solving practical multi-objective optimization problems was demonstrated.
Optimization, differential evolution, Pareto theory, MOEA/D, NSGA, mutation
Короткий адрес: https://sciup.org/148321669
IDR: 148321669 | УДК: 591.87 | DOI: 10.31772/2587-6066-2019-20-2-134-143
Текст научной статьи The development and investigation of the efficiency of the differential evolution algorithm for solving multi-objective optimization problems
Introduction. Complex technical and organizational systems control requires constant decision making taking into consideration various criteria and limited resources. Such kind of problems (multi-objective optimization problems) can be found in different areas, including aerospace industry (for example, [1–3]). For some of them it is possible to find solutions, which would be optimal with respect to all criteria. However, the opposite situation, namely when the criteria conflict with each other, occurs more frequently. In that case there is s a need to determine a set of solutions (best possible variants), where each one of them can be considered as a compromise between all criteria.
There are various ways to determine the mentioned set of solutions, but the most popular among them is the Pareto dominance theory [4]. Generally speaking, a multiobjective optimization problem includes a set of D parameters (variables), a set of K objective functions of these variables, and a set of M constraints. It is necessary to find a solution, that is optimal according to all K criteria, while solving a multi-objective optimization problem; and the problem is formulated as follows:
y = f ( x ) = ( f ( x ) , f 2 ( x ) ,-, fK ( x ) ) ^ opt , (1)
gj (x)^ 0, j = 1, r, hj (x ) = 0, j = r +1, M,
where x = ( x 1 ,x 2 ,..., xD ) is possible solution.
Let us consider the multi-objective unconstrained optimization problems. Generally, there are no additional requirements of functions f ( x ) , i = 1, ^, K , that would be convenient for optimization (for example, convexity, differentiability, etc.). Functions can be defined algorithmically; variables can be continuous, discontinuous, binary and even mixed. This fact significantly reduces the class of optimization algorithms, which could be applied to solving such problems.
In this study modifications of the Differential Evolutions (DE) algorithm [5] for solving multi-objective opti-
mization problems based on the well-known schemes such as MOEA/D (Multiobjective Evolutionary Algorithm Based on Decomposition) [6] and NSGA (Nondominated Sorting Genetic Algorithm) [7], that use the Pareto theory, are introduced. Moreover, efficiency of these modifications was examined in accordance with the chosen DE’s mutation operator [8].
Differential Evolution. Differential evolution or DE is a population-based meta-heuristic approach initially developed for solving multidimensional optimization problems. It was firstly introduced by K. Price and R. Storn in 1995 [5] for solving single-objective optimization problems. The DE algorithm is a direct optimization method, thus it only needs values of the objective function; it uses some of ideas the proposed for the genetic algorithms such as mutation as well.
The DE starts with the random initialization of the population that contains N individuals, to be more specific the set of N vectors is randomly generated. Each individual is represented by its coordinates in the search space with D dimensions. Then a new generation is created in the following way. For each individual xit three different vectors from the old generation are randomly chosen, after that a new mutant vector vit is generated by using the mutation operator.
Nowadays there are various mutation schemes for the differential evolution algorithm [8]. In this study five most popular mutation strategies were used ( rand , best , current_to_best , best2 , rand2 ):
v j = xR 1, j + F ( xR 2, j - x R 3, j ) ; (3)
v j = x best , j + F ( xR 1, j - xR 2, j ) ; (4)
tt t t t t vj = xi, j + F (xbest, j - xi, j ) + F (xR 1, j - xR2, j ) ; (5) vj = xbest, j + F (xR 1, j - xR2, j ) + F (xR3, j - xR4, j ) ; (6)
v t j
= x R 1, j
+ F ( x R 2, j
-
x R t 3, j
) + F ( xR4, j
-
xR 5, j ) .
In these formulas indexes R 1, R 2, R 3, R 4 and R 5 are numbers randomly chosen from the range [1, N ], all of them differ from the index i and each other; F is the scaling factor, namely the maximum possible distance by which the search area can be expanded in one variable; xbtest – the best position found by the population during t iterations.
The next step is the crossover, which is performed for the mutant vector. During the crossover its coordinates (or at least a part of them) can be replaced with some probability ( CR ) by the coordinates of the parent vector. A new obtained vector is called a trial vector. If the value of the objective function calculated for the trial vector is better than the value of the objective function calculated for the parent vector, then the parent vector should be replaced by the trial vector in a new generation, otherwise it stays the same.
Modifications of the DE algorithm for solving multi-objective optimization problems. In this study two well-known schemes for the multi-objective optimization problems were used: Multiobjective Evolutionary Algorithm Based on Decomposition (MOEA/D) [6] and Non-dominated Sorting Genetic Algorithm (NSGA) [7].
Modification of the DE algorithm based on the scheme NSGA works as follows. First of all, in addition to the population of individuals an external archive is generated, in which optimal according to the Pareto theory solutions are saved. This archive is updated at each iteration.
Besides, on every iteration during the crossover the additional second archive of size 2 N , in which initially all individuals from the population are stored, is created. As was mentioned before, during crossover trial vectors, that can replace parent individuals in population, are generated. If the parent individual from the second additional archive is non-dominant with respect to the respective trial vector then the latter is discarded and the parent individual stays the same, and vice versa, if the trial vector is non-dominant then it replaces the parent vector in the second archive. However, if the parent and trial vectors are not comparable then they both are stored in the second additional archive. It should be noted that the trial vectors, which are stored in the mentioned archive, later participate in the crossover, and for them the mutant vectors are generated by using individuals saved in the same archive.
On the next step the second additional archive is truncated to the size N by using the sorting of individuals according to the degree of their non-dominance proposed for the NSGA scheme [7]. Individuals are sorted in the mentioned archive as follows. For each individual its rank, which is denoted as “ rank ”, is determined. If an individual is non-dominant with respect to all other individuals from that archive then its rank = 0. After that the individual, which is non-dominant with respect to all other individuals from archive except the one with the rank = 0, is determined. Therefore, its rank is assigned to 1. If there are more than one such an individual, then the same rank is assigned to each of them. The process continues until all individuals in the population are ranked.
Next, the ranked individuals are selected according to the Crowding-distance metric ( I ) described in [9]. For each objective function the solutions with the smallest and largest values of this metric are determined. It is assumed that the metric value for these solutions from the second additional archive reaches its maximum. For other solutions from the archive the distance (metric value) is calculated as follows:
K
I [ i ] = Z k = 1
f k [ i + 1 ] - f k [ i - 1 ] max min Jk Jk
Here parameters fk max and fk min are the maximum and the minimum values of the k -th objective function, fk [ i + 1 ] and fk [ i - 1 ] are values of the k -th objective function for the ( i + 1)-th and ( i – 1)-th individuals respectively.
After that, the i -th individual is compared with the rest ( i = 1, ..., 2 N ) until it is better than any individual according to the rank or to the value of the metric (the higher, the better). In this case, it is saved in a truncated archive, the comparison is stopped and the next individual is considered. These actions are repeated until the number of individuals in the truncated archive is equal to N .
The external archive, in which non-dominated solutions are stored, is updated by the individuals stored in the additional archive. The population that consists of individuals from the truncated archive passes to the next generation.
Now let us consider the modification of the DE algorithm, developed on the basis of the MOEA/D scheme [6]. As for the previous modification, initially an external archive for the non-dominated solutions according to the Pareto theory is generated; moreover, this archive is updated at each iteration. Further, the population of N individuals is initialized randomly.
For each i -th ( i = 1, ..., N ) individual, the vector L i consisting of weight coefficients for the corresponding objective functions (one coefficient per objective function) is generated. The coefficients are generated randomly within the range [0, 1] and vector L i is normalized.
Next, the reference vector z = ( z 1 , z 2 ,..., zK ) , where Z j is the best currently found value of the j -th ( j = 1, …, K ) objective function f j , is determined. In addition, for each i -th individual, a set of indexes B ( i ) is created, it consists of T indexes of the nearest to L i neighbors, to be more specific the distances between the vectors L i and L j ( j = 1, …, N and j ≠ i ) are calculated using the Euclidean metric, and then T indexes of the nearest neighbors are selected.
Thus, for each i -th individual, where i = 1, …, N , the set of indexes B ( i ) = { i (1), …, i ( T )} is defined such as L i (1), …, L i ( T ) are the T closest vectors to the vector L i . Then, during the mutation for the described schemes (3)–(7) indexes R 1, R 2, R 3, R 4, R 5 for the i -th individual are randomly chosen from the set B ( i ).
At the crossover step the trial vector U is generated, after that the vector z is updated. Finally, according to the rule described in [6] the individual in the population is updated (it is replaced by the trial vector U ).
Experimental results. The investigation into the efficiency of the DE algorithm with different mutation strategies and schemes for the multi-objective optimization problems was conducted by using the following test problems: ZDT1, ZDT2, ZDT3, ZDT6, Schaffer’s Min-Min (SCH) and DTLZ2 [10]. The following parameters were used for testing:
-
1) S – the maximum number of optimal according to the Pareto theory solutions, which were saved during the algorithm’s work; it was set to 100;
-
2) N – the population size, it was equal to 100;
-
3) MaxGen – the maximum number of iterations equal to 250;
-
4) F = 0.4;
-
5) CR = 0.3 for modification of the DE approach based on the MOEA/D scheme;
-
6) CR = 0.6 for modification of the DE approach based on the NSGA scheme;
-
7) T = 20;
-
8) D = 30.
Each problem was solved by all modifications 10 times and after each program run the following values were calculated: the E f error (i. e. the difference between the obtained and real Pareto fronts) and the spread ∆ (i. e. the extend of spread achieved among the obtained solutions).
The E f error was calculated by using the following formula (9):
2 NS 2
E f =| PF e - PF t\\ = £ ( PF j - PF j ) , (9)
j = 1
where PFe is the found Pareto front, PFt is the actual Pareto front, NS is the number of points in the external archive. The value of the spread ∆ was determined using the following formula:
NS — 1
df + di + X \ii - d|
A =-----------/=1-----, (10)
df + dl + (NS-1) d where di is the minimal Euclidean distance between the i-th solution from the obtained Pareto front and other solutions from that front [11] (NS – number of solutions in the external archive), and d is the average distance. Parameters df and dl are Euclidean distances between the extreme solutions of the real and obtained Pareto fronts.
Results obtained by the modification of the DE algorithm based on the MOEA/D scheme with different mutation strategies and averaged by the number of program runs are presented in tab. 1.
Thus, it was established that modification of the DE approach based on the MOEA/D scheme demonstrated the best results while using the mutation strategy best . Tab. 2 shows how many times this algorithm configuration outperformed others according to four criteria: Best – the best obtained values of E f and ∆ respectively, Worst – the worst values, Mean – the mean values for E f and ∆, SD is the standard deviation for the obtained results.
Results obtained by the modification of the DE algorithm based on the NSGA scheme with different mutation strategies are presented in tab. 3.
Results obtained by the DE+MOEA/D algorithm with different mutation schemes
Table 1
|
Problem |
rand |
best |
current_to_best |
best 2 |
rand 2 |
|
|
ZDT1 |
E f |
0.00384 |
0.00054 |
6.59454 |
0.00119 |
0.0062 |
|
∆ |
0.16367 |
0.11775 |
0.489 |
0.13324 |
0.16509 |
|
|
ZDT2 |
E f |
0.00053 |
0.00041 |
5.92685 |
0.00055 |
0.00199 |
|
∆ |
0.09408 |
0.11174 |
0.70551 |
0.105 |
0.11352 |
|
|
ZDT3 |
E f |
0.15176 |
0.08976 |
4.84475 |
0.0003 |
0.00249 |
|
∆ |
0.19449 |
0.16297 |
0.43173 |
0.09944 |
0.15936 |
|
|
ZDT6 |
E f |
2.08E-07 |
2.05E-07 |
0.47384 |
2.03E-07 |
0.00391 |
|
∆ |
0.04915 |
0.44263 |
0.63503 |
0.04259 |
0.02977 |
|
|
SCH |
E f |
6.85E-07 |
7.19E-07 |
0.00019 |
0.01249 |
7.19E-07 |
|
∆ |
0.40399 |
0.30593 |
0.36606 |
0.32616 |
0.35382 |
|
|
DTLZ2 |
E f |
0.00024 |
0.00022 |
2.62E-05 |
0.00056 |
0.00038 |
|
∆ |
0.05619 |
0.06844 |
0.0706 |
0.10307 |
0.07852 |
|
Table 2
The results of the comparison of the mutation schemes for the DE+MOEA/D modification
|
Scheme |
E f |
∆ |
||||||
|
Worst |
Best |
Mean |
SD |
Worst |
Best |
Mean |
SD |
|
|
rand |
0 |
1 |
1 |
0 |
1 |
0 |
2 |
1 |
|
best |
3 |
4 |
2 |
3 |
1 |
3 |
4 |
1 |
|
current_to_best |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
|
best2 |
2 |
0 |
2 |
2 |
3 |
2 |
1 |
3 |
|
rand2 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
Thus, it was established that the strategy best demonstrated the best results comparing to others in 10 cases, while the strategy rand in 14 cases. However, for this modification strategy rand outperforms the strategy best because it showed the better results according to the second criterion (spread of solutions along the front) more frequently. Tab. 4 shows how many times this algorithm configuration outperformed others according to four criteria: Best – the best obtained values of E f and ∆ respectively, Worst – the worst values, Mean – the mean values for E f and ∆, SD is the standard deviation for the obtained results.
Examples of the Pareto fronts obtained by the developed modifications of the DE algorithm with determined on the previous step best mutation strategies for the listed test problems are demonstrated in fig. 1–6.
The developed modifications of the DE algorithm (DE + NSGA and DE + MOEA/D) are compared with the other methods for solving multi-objective optimization problems: MOPSO [12], NSGA-II [13], SPEA [14] and PAES [15]. Moreover, the comparison was made according to the previously used criteria (error and variation).
Tab. 5 shows the mean values for the criteria obtained by the listed algorithms. The results of the NSGA-II and SPEA, PAES algorithms are taken from the literature [15], and the results of the MOPSO algorithm were obtained independently.
Table 3
Results obtained by the DE+NSGA algorithm with different mutation schemes
|
Problem |
rand |
best |
current_to_best |
best 2 |
rand 2 |
|
|
ZDT1 |
E f |
0.00733 |
0.00884 |
0.00577 |
0.02993 |
0.03549 |
|
∆ |
0.0775 |
0.07231 |
0.28125 |
0.07318 |
0.06684 |
|
|
ZDT2 |
E f |
0.00627 |
0.00311 |
0.31043 |
0.0197 |
0.03744 |
|
∆ |
0.10933 |
0.603442 |
0.75164 |
0.11818 |
0.12551 |
|
|
ZDT3 |
E f |
0.00491 |
0.00628 |
0.00277 |
0.0259 |
0.44998 |
|
∆ |
0.06465 |
0.07346 |
0.59455 |
0.0817 |
0.16594 |
|
|
ZDT6 |
E f |
0.00058 |
2.90E-07 |
0.00212 |
3.25E-07 |
0.00324 |
|
∆ |
0.05462 |
0.03373 |
0.05722 |
0.0548 |
0.06761 |
|
|
SCH |
E f |
4.93E-05 |
5.69E-06 |
5.66E-07 |
0.00041 |
7.7E-07 |
|
∆ |
0.10595 |
0.17782 |
0.18019 |
0.11755 |
0.10743 |
|
|
DTLZ2 |
E f |
11.1832 |
6.6664 |
12.164 |
4.91719 |
0.01469 |
|
∆ |
0.417295 |
0.27964 |
0.542015 |
0.20289 |
0.05895 |
|
Table 4
The results of the comparison of mutation schemes for the DE+NSGA modification
|
Scheme |
E f |
∆ |
||||||
|
Worst |
Best |
Mean |
SD |
Worst |
Best |
Mean |
SD |
|
|
rand |
2 |
1 |
1 |
2 |
2 |
1 |
3 |
2 |
|
best |
1 |
1 |
2 |
1 |
1 |
1 |
1 |
2 |
|
current_to_best |
1 |
4 |
2 |
0 |
0 |
0 |
0 |
0 |
|
best2 |
1 |
0 |
0 |
1 |
2 |
3 |
0 |
1 |
|
rand2 |
1 |
0 |
1 |
2 |
1 |
1 |
2 |
1 |
Based on scheme NSGA Based on scheme MOEA/D
Fig. 1. Examples of the Pareto front obtained for the ZDT1 problem
Рис. 1. Примеры фронта Парето, полученные для задачи ZDT1
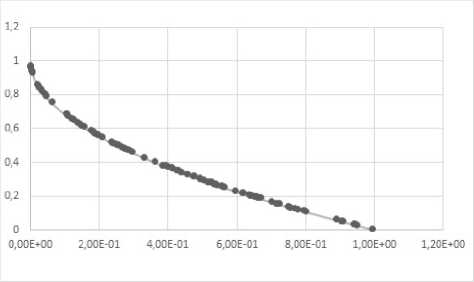
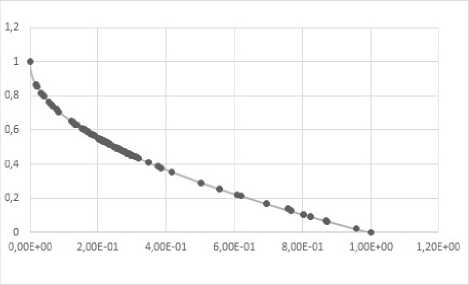
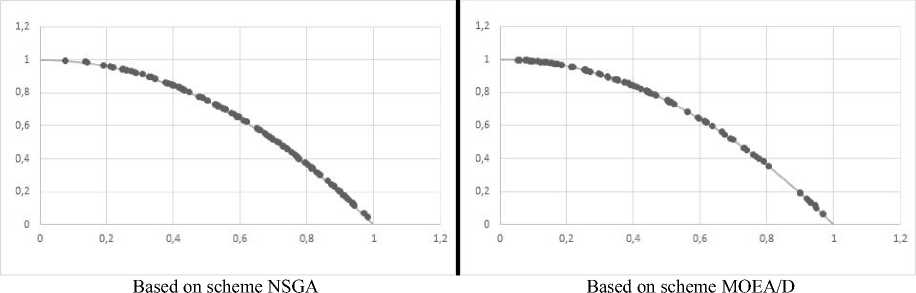
Fig. 2. Examples of the Pareto front obtained for the ZDT2 problem
Рис. 2. Примеры фронта Парето, полученные для задачи ZDT2
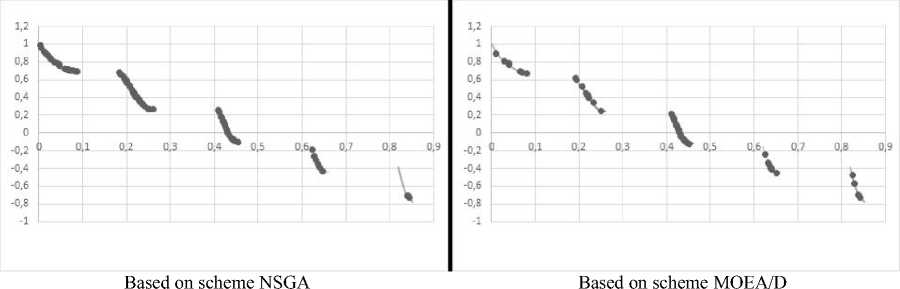
Fig. 3. Examples of the Pareto front obtained for the ZDT3 problem
Рис. 3. Примеры фронта Парето, полученные для задачи ZDT3
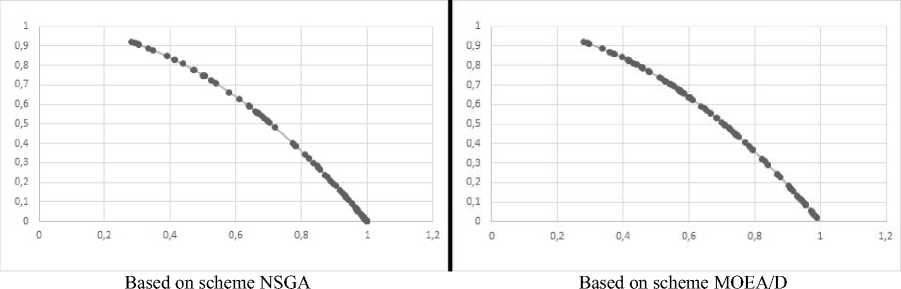
Fig. 4. Examples of the Pareto front obtained for the ZDT6 problem
Рис. 4. Примеры фронта Парето, полученные для задачи ZDT6
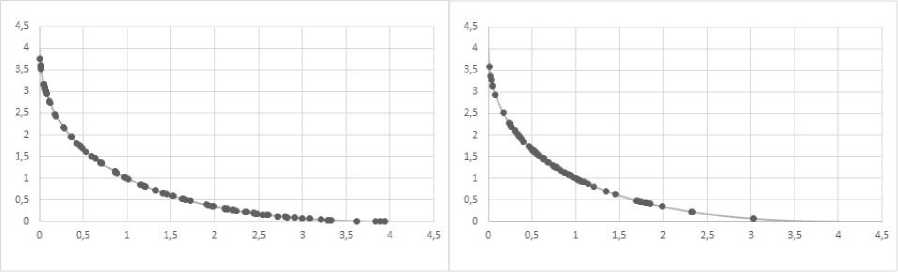
Based on scheme NSGA Based on scheme MOEA/D
Fig. 5. Examples of the Pareto front obtained for the SCH problem
Рис. 5. Примеры фронта Парето, полученные для задачи SCH
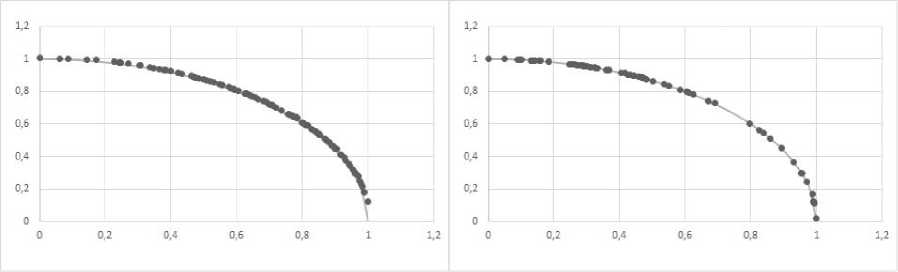
Based on scheme NSGA
Based on scheme MOEA/D
Fig. 6. Examples of the Pareto front obtained for the DTLZ2 problem
Рис. 6. Примеры фронта Парето, полученные для задачи DTLZ2
The results of the comparison of the algorithms for solving multi-objective optimization problems
Table 5
|
Algorithm |
ZDT1 |
ZDT2 |
ZDT3 |
ZDT6 |
SCH |
|||||
|
E f |
∆ |
E f |
∆ |
E f |
∆ |
E f |
∆ |
E f |
∆ |
|
|
NSGA-II-r |
0.0335 |
0.3903 |
0.0724 |
0.4308 |
0.1145 |
0.7385 |
0.2966 |
0.668 |
0.0034 |
0.4779 |
|
NSGA-II-b |
0.0009 |
0.4633 |
0.0008 |
0.4351 |
0.0434 |
0.5756 |
7.8068 |
0.6445 |
0.0028 |
0.4493 |
|
SPEA |
0.0018 |
0.7845 |
0.0013 |
0.7551 |
0.0475 |
0.6729 |
0.2211 |
0.8494 |
0.0034 |
1.0211 |
|
PAES |
0.0821 |
1.2298 |
0.1263 |
1.1659 |
0.0239 |
0.7899 |
0.0855 |
1.1531 |
0.0013 |
1.0633 |
|
MOPSO |
0.0605 |
0.5685 |
0.0807 |
0.4045 |
0.0016 |
0.415 |
0.0015 |
0.1204 |
8.91E-07 |
0.6039 |
|
DE+NSGA |
0.0073 |
0.0775 |
0.0063 |
0.1093 |
0.0049 |
0.0646 |
0.5706 |
0.1977 |
4.93E-05 |
0.1059 |
|
DE+MOEA/D |
0.0005 |
0.1177 |
0.0004 |
0.1117 |
0.0898 |
0.163 |
2.05E-07 |
0.4426 |
7.19E-07 |
0.3059 |
Thus, as a result of the research, it is established that the best values of objective functions are achieved by modifying the algorithm of differential evolution based on the NSGA scheme with the simplest mutation strategy called rand . Moreover, the experiments demonstrate that the modification of the DE algorithm of the NSGA scheme approximates the Pareto front better than the other multi-objective optimization algorithms, namely MOPSO, PAES, NSGA-II, SPEA, DE + MOEA / D.
The problem of the choice of spacecraft control contour variant. In this study the problem of the choice of spacecraft’s control contour variant [16] is considered. The functioning process of a spacecraft control subsystems is modeled with Markov chains, while the problem of choosing an effective variant for a spacecraft control system is formulated as a multi-objective discrete optimization problem with algorithmically given functions.
The problem statement and the way the problem of spacecraft’s control contour variant choice was modeled are presented in [16]; in this study only a brief description is given.
The system for monitoring and control of an orbital group of telecommunication satellites includes on-board control complexes (BCC) of a spacecraft, a distributed system of telemetry, command and ranging (TCR) stations and data telecommunication systems in each, command measuring systems (CMS) and flight control center (FCC). It should be noted that the last three subsystems are combined into the ground-based control complex (GCC).
Thus, the ground control complex interacts with the onboard control complex using a telecommunication system, as well as command measuring systems and data transmission systems, which include communication centers of a flight control center. BCC is the controlling subsystem of the satellite that ensures real time checking and controlling of on-board systems including pay-load equipment as well as fulfilling program-temporal control. Control functions performed by the automated control system can be divided into subsystems called “control contours”. Mentioned contours perform various functions, for example the following contours can be distinguished: a technological contour, a command-program contour, a target contour, etc. [16].
The main task of the command-program contour is the maintenance of the tasks of creating commandprogramming information, transmitting it to BCC and executing it and control action as well as the realization of the temporal program mode of control. Let us consider the simplified control system, which consists of three subsystems: onboard target equipment, on-board control complexes and ground-based control complex.
If we suppose that BCC can fail and GCC is absolutely reliable, then we can introduce the following notations: λ 1 is the intensity of BCC failures, μ 1 is the intensity of temporal program (TP) computation, μ 2 is the intensity of the command-programming information (CPI) loading into BCC, μ 3 is the intensity of temporal program execution, μ 4 is the intensity of BCC being restored. Therefore, all stochastic flows in the system are Poisson, and there are five possible states for this contour [16]:
-
1) BCC fulfills TP, GCC is free;
-
2) BCC is free, GCC computes TP;
-
3) BCC is free; GCC computes CPI and loads TP;
-
4) BCC is restored with GCC which is waiting for continuation of TP computation;
-
5) BCC is restored with GCC which is waiting for continuation of CPI computation.
The corresponding Kolmogorov system of equations for the final probabilities is the following:
Pi■(Xi + Ц3 )-ц2 ■ P = 0,(11)
P2 -(Ц1 + X1 )-Цз ■ P-^4 ■ P4 = 0,
P-(Xi +Ц2 )-^ ■ /2-Ц4 ■ P5 = 0,(13)
P4 .щ-Xi ■ Pi-Xi ■ P, = 0,(14)
P5 -Ц4 -X1 ■ P3 = 0 ,
Pi+P,+P3 + P4+P5=1.(16)
In these formulas P i is the probability that the system is in the i -th state, where i = 1, …, 5. After solving the system (11)–(16), the necessary indexes of control quality for the command-programming contour can be calculated:
P
-
1) T = —1--the average duration of the independ- Ц , ■ P
ent operating of the spacecraft for this contour;
P + P , . .
-
2) tx = —--- 5 - the average duration of BCC and Ц 1 ■ P ,
GCC interactions when loading TP for the next interval of independent operation of the spacecraft;
P, + P + P, + P
-
3) t 2 = ——7---4——5 - the average time from the
Pi ■(Xi +Ц3)
start of TP computation till the start of TP fulfillment by BCC.
Maximizing the first indicator and minimizing the last two indicators leads to the choosing of an effective variant for a spacecraft control system. Thus, the multiobjective optimization problem is formulated with three objective functions. In this study it was solved by the best developed configurations of the DE+NSGA and DE+MOEA/D algorithms. The examples of the obtained Pareto fronts for the described optimization problem are presented in the fig. 7, to be more specific the projection of the Pareto front on the plane μ 2 – μ 4 (μ 2 – horizontal axis, μ 4 – vertical axis). In addition, on the graphs, the solid points are the points from the Pareto set, obtained by the algorithm, the open points are the true set points (not found respectively).
The problem was solved by each algorithm 10 times, for each program run the number of iterations was set to 30, number of individuals to 20, and for the DE+MOEA/D algorithm parameter was equal to 5. As a result of the research, it was established that modification of the DE algorithm based on the NSGA scheme (DE+NSGA) with the previously found configuration is able to solve the described problem of the choice of spacecraft control contour variant better. Therefore, the workability of that algorithm was verified on real-world problem.
Conclusions. In this paper two developed modifications of the differential evolution algorithm based on the schemes NSGA (DE+NSGA) and MOEA/D (DE+MOEA/D) for solving multi-objective optimization problems are described. First of all, the efficiency of the proposed modifications was examined in accordance with the selected mutation strategy: it was established that for the DE+NSGA algorithm the most useful is the rand mutation strategy, while for the DE+MOEA/D algorithm it is the best strategy.
Then the results obtained by modifications of the differential evolution algorithm with defined mutation strategies were compared with the results obtained by other well-known population-based algorithms. Finally, it was proved that the modification DE+NSGA described in this study with the rand mutation strategy outperforms alternative algorithms for solving multi-objective optimization problems.
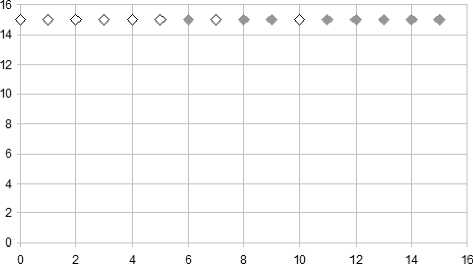
Based on scheme NSGA Based on scheme MOEA/D
Fig. 7. Examples of the Pareto set obtained for the problem of the spacecraft control contour variant choice
Рис. 7. Примеры множества Парето, полученные для задачи выбора эффективного варианта управления КА
Besides, the problem of the choice of spacecraft control contour variant was solved and the workability of the proposed approaches was demonstrated on the real-world problem.
Acknowledgment. This research is performed with the financial support of the Ministry of Education and Science of the Russian Federation in the frame of the state assignment № 2.6757.2017/БЧ.
Список литературы The development and investigation of the efficiency of the differential evolution algorithm for solving multi-objective optimization problems
- Semenkina M., Akhmedova Sh., Brester Ch. et al. Choice of spacecraft control contour variant with selfconfiguring stochastic algorithms of multi-criteria optimization. Proceedings of the 13th International Conference on Informatics in Control, Automation and Robotics (ICINCO’2016). 2016, P. 281–286.
- Semenkina M., Akhmedova Sh., Semenkin E. et al. Spacecraft solar arrays degradation forecasting with evolutionary designed ANN-based predictors. Proceedings of the 11th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2014). 2014, P. 421–428.
- Akhmedova Sh., Semenkin E. Co-operation of biology related algorithms for multiobective optimization problems. Proceedings of the International Conference on Computer Science and Artificial Intelligence (ICCSAI). 2014.
- Podinovskij V., Nogin V. Pareto-optimalnye resheniya mnogokriterialnyh zadach [Pareto Optimal Solutions of the Multiobjective Problems]. Moscow, Nauka Publ., 1982, 256 p.
- Storn R., Price K. Differential evolution – a simple and efficient heuristic for global optimization over continuous spaces. Journal of Global Optimization. 1997, Vol. 11, No. 4, P. 341–359.
- Zhang Q., Li H. MOEA/D: A multiobjective evolutionary algorithm based on decomposition. IEEE Transactions on Evolutionary Computation. 2007, Vol. 11, Iss. 6, P. 712–731.
- Srinivas N., Deb K. Multi-objective function optimization using nondominated sorting genetic algorithms. Evolutionary omputation. 1994, Vol. 2, No. 3, P. 221–248.
- Das S., Suganthan P. N. Differential evolution: A survey of the state-of-the-art. IEEE Transactions on Evolutionary Computation. 2011, Vol. 15, Iss. 1, P. 4–31.
- Deb K., Jain S. Running Performance metrics for evolutionary multi-objective optimization. Proceedings of the 4th Asia-Pacific Conference on Simulated Evolution and Learning (SEAL’02). 2002, Vol. 1, P. 13–20.
- Zitzler E., Thiele L. An evolutionary algorithm for multiobjective optimization: The strength pareto approach. Technical Report 43, Computer Engineering and Networks Laboratory (TIK), Swiss Federal Institute of Technology (ETH) Zurich. 1998.
- Ah King R. T. F., Deb K., Rughooputh H.C.S. Comparison of NSGA-II and SPEA2 on the multiobjective environmental/economic dispatch problem. University of Mauritius Research Journal. 2010, Vol. 16, P. 485–511.
- Moore J., Chapman R. Application of particle swarm to multiobjective optimization. Technical Report, Department of Computer Science and Software Engineering, Auburn University, 1999.
- A fast and elitist multiobjective genetic algorithm: NSGA–II / K. Deb, A. Pratap, S. Agarwal et al. IEEE Transactions on volutionary Computation. 2002, Vol. 6, P. 182–197.
- Zitzler E., Thiele L. Multiobjective evolutionary algorithms: A comparative case study and the strength Pareto approach. IEEE Transactions on Evolutionary Computation. 1999, Vol. 3, No. 4, P. 257–271.
- Knowles J. D., Corne D. W. The Pareto archived evolution strategy: A new baseline algorithm for Pareto multiobjective optimization. Proceedings of the IEEE Congress on Evolutionary Computation. 1999, Vol. 1, P. 98–105.
- Semenkina M., Akhmedova Sh., Brester C., Semenkin E. Choice of spacecraft control contour variant with self-configuring stochastic algorithms of multicriteria optimization. Proceedings of the 13th International Conference on Informatics in Control, Automation and Robotics. 2016, Vol. 1, P. 281–286.


