The effect of reliability index values on resulting reliability-based topology optimization configurations: numerical validation by shape optimization

Optimizing the topology seeks to answer one of the first questions regarding the nature of the structure in order to meet the required specifications. So the problem of topology is to determine the general characteristics of the studied structure, and the purpose of topology optimization is to make this initial choice as au- tomatic as possible [1]. In addition, both macroscopic structures and microscopic materials can be found using topology optimization concepts. In other words, it is not only the optimal spatial distribution of the material on the macroscopic structural scale, but also the optimal local use of the cellular material on the microscopic scale1.

Two basic topology optimization models can be classified in the literature: deterministic and reliability-based models. In Deterministic Topology Optimization (DTO), one can search for a single solution for a given domain2. But the Reliability-Based Topology Optimization (RBTO) model studied in this article, can lead to several solutions with different advantages, allowing us to choose the best topology to meet the technical specifications. The structural weight of the solutions obtained using this model is reduced in comparison with the DTO model. In addition, when using the RBTO model, the obtained layout is more reliable in comparison with the deterministic topology at the same weight values3. To develop this model, two points of view are presented: topology optimization and reliability analysis. A literature review is presented in the next section to show the various advantages of the RBTO model. As result, several reliability-based topologies are obtained when considering several reliability levels. To compare the resulting topologies, a shape optimization is considered and shows that for the same boundary conditions, the RBTO configurations reduce the structural weight when increasing the reliability index values.

Literature Review

The main difference between DTO and RBTO is to consider the uncertainty on the parameters having important roles for optimal topology. The main idea of reliability-based topology optimization is based on the reliability-based design optimization. When considering the reliability-based design optimization problem, the uncertainties regarding variable sizes are taken into account to ensure greater reliability of the proposed solution. However, the reliability-based topology optimization aims to provide designers with several solutions that have several levels of reliability. Here the designer can choose the best solution. In the RBTO model, several methods have been developed. The different works can be divided into two points of view.

From point of view “topology optimization”, the reliability-based topology optimization model was developed in the article of G. Kharmanda and N. Olhoff4 to provide the designer with multiple reliability-based structures, but in the classical topology optimization, the designer produces only one deterministic topology. It is shown that the importance of the reliability-based topology optimization model leads to structures that are more robust than those obtained by deterministic topology optimization for the same weight [2–4]. In addition, probabilistic neural networks in the case of highly nonlinear or disjoint problems of the failure region are used in some studies [5]. This strategy has been successfully applied on various trusses. Recently, a method of optimization of the topology of detailed design of solid structures based on probabilistic reliability has been developed5.

From a point of view “reliability analysis”, deterministic topology optimization is formulated as finding the most rigid structural arrangement with volume restriction. To maintain rigidity stability in topological design, optimization prob- lem is formulated as a volume minimization problem with displacement restriction and RBDO technique is applied6. Here, the objective is to minimize the structural volume under the condition of the linear limit state function. Further, in article of H. Agarwal7 a hybrid cellular automaton (HCA) was developed for the structural synthesis of a continuum material, where the state of each cell is determined by both density and strain energy. The paper [6] uses an unrelated RBDO approach in which topology optimization is separated from reliability analysis. The use of RBTO taking into account the gradient free hybrid cellular automata (HCA) method was performed8. Here, the formulation also includes uncertainty about material properties. The RBTO model using bidirectional evolutionary structural optimization and the standard response surface method was performed [7]. A computational method for reliability-based topology optimization for continuous domain under uncertainty of material properties has been developed [8].

Comparing both different points of view, the computing time of the reliabilitybased topology optimization methods in terms of “reliability analysis” is very high since a large number of design variables are associated with optimization problems of the continuum topology9.

Thus, the point of view “topology optimization” seems to be very interesting to topology developers because it leads to several reliability-based structures with respect to changes in the reliability index. It produces different structures while when considering the point of view “reliability analysis”, we get the same structure with different densities that makes no sense for the next detailed design stages.

To perform RBTO tasks, some RBDO methods can be used since we deal with a different definition or philosophy. Several RBDO methods have been developed with respect to their use10 [9]. The gradient-based method seems very easy to use, especially when considering static cases [2; 3]. In this work, a gradient-based method is used to create several reliabilitybased topologies. The resulting models are considered as the input configuration of the shape optimization algorithm in order to show their different advantages.

Materials and Methods

Deterministic Topology Optimization

The problem of topology optimization is related to the minimization of strain energy under the condition of limiting the structural volume [10]. All load parameters and material properties are treated as deterministic values. The topology optimization problem consists of minimizing the compliance with a target percentage of the structural volume. This problem can be mathematically expressed [11]:

min: Comp s..: V £

V >"

f t ,

where Comp is the compliance considering the material densities in each element as optimization variables that belong to the interval [0, 1]. V0 and V are the initial-and current structural volume values. Formulation (1) is a basic form and can be used with several topology optimization methods such as SIMP (Solid Isotropic Microstructure with Penalty), homogenization approach [11; 12]. In this work, SIMP method is considered. Equation (1) can be expressed by:

N min :C(x) = qTKq = £(xe)pqTkoqe e=1

s.t.: V x = f

V

V ₀

: Kq = F

^{: 0} < x min ^ x ^ 1,

where q and F are the global displacement and force vectors, respectively. K is the global stiffness matrix. q_e and k₀ are the element displacement vector and stiffness matrix, respectively. X is the vector of design variables; x_min is a vector of minimum relative densities (non-zero to avoid singularity). N is the number of elements to discretize the design domain. p is the penalization power. V ( x ) and V₀ are the material volume and design domain volume, respectively and f is the prescribed volume fraction.

Reliability-Based Topology Optimization

In deterministic structural optimization, the designer seeks to reduce construction costs without taking into account the effects of material uncertainty, geometry, and load. In this case, the resulting optimal configurations can represent a lower level of reliability and then result in a higher failure rate. The balance between minimizing costs and maximizing reliability is a big challenge for the designer. The importance of reliability criteria in deterministic design optimization is to increase the level of design reliability without significantly increasing its weight. Thus, when the concept of reliability is integrated into the optimization of size and/or shape [13; 14], the model is called Reliability-Based Design Optimization (RBDO)11, which allows to design structures that meet the requirements of economy and security. However, when introducing reliability analysis to topology optimization, the non-quantitative nature is taken into account. This model is called Reliability-Based Topology Optimization (RBTO). The goal of the RBTO model is to address some of the uncertainties in geometry or design load by introducing reliability criteria into the optimization procedure. This integration takes into account the randomness of the applied loads and the description of the geometry. The RBTO task can be written as [11]:

min: Comp s .t.: в ^ P,

V and :^ ^ ft, V 0

where β and β_t are the structural reliability index and the target reliability index, respectively (for more information about reliability methods, see¹² [15]). Considering that SIMP method is implemented, Equation (3) can be written as:

N min : C (x) = qr Kq = ^(xe)p qfk oq e e=1

s.t.: p ( u ) >  p t

: K(x, y,u) • q(x, y,u) = F(y,u)   (4)

V (x, y, u)

:          = f (y,u)

V _o

* min

The integration of reliability analysis into the topology optimization has been carried out by performing gradient-based method for static studies [3].

Reliability index effect on resulting reliability-based topologies

When considering deterministic topology optimization, we can modify the nature of the structure more profoundly. This way the geometry of the part is envisaged without any prior requirement as to the domains and/or the connections of the structural elements present in the solution. The topology optimization involves, in one way or another, the determination of the shape or transverse dimensions of the structure, so certain some authors also call it generalized shape optimization [16–19]. Reliability-Based Topology Optimization has the objective to introduce reliability analysis into topology optimization in order to generate several topologies relative to the values of the reliability index. In our study13, the relationship between the objective function (compliance) and the reliability index for the four studied structures14. As results, the complexity of the geometry and the multiple loading of the structures play a very important role relative to the reliability index variability, which enables the designer to choose the best solution out of the different topologies obtained by Reliability-Based Topology Optimization. However, there is no validation concern- ing the importance of this changes. Therefore, we seek in this works to use the shape optimization to test several layouts.

Results

TOPOLOGY OPTIMIZATION RESULTS

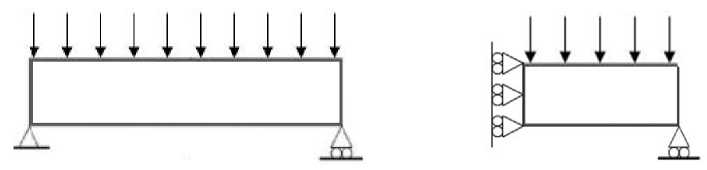
We consider an MBB (Messerschmitt-Bölkow-Blohm) [20; 21] beam subject to a distributed load as an example for this numerical demonstration (Fig. 1). Figure 1a shows a full design domain of the studied beam with all boundary conditions while Figure 1b illustrates the equivalent symmetry boundary conditions of a half beam.

The random input parameters are: the number of elements of meshing model, in directions x and y ( nelx = 40 and nely = 40), the volume fraction ( volfrac = 0,5) and the distributed load ( P = –1).

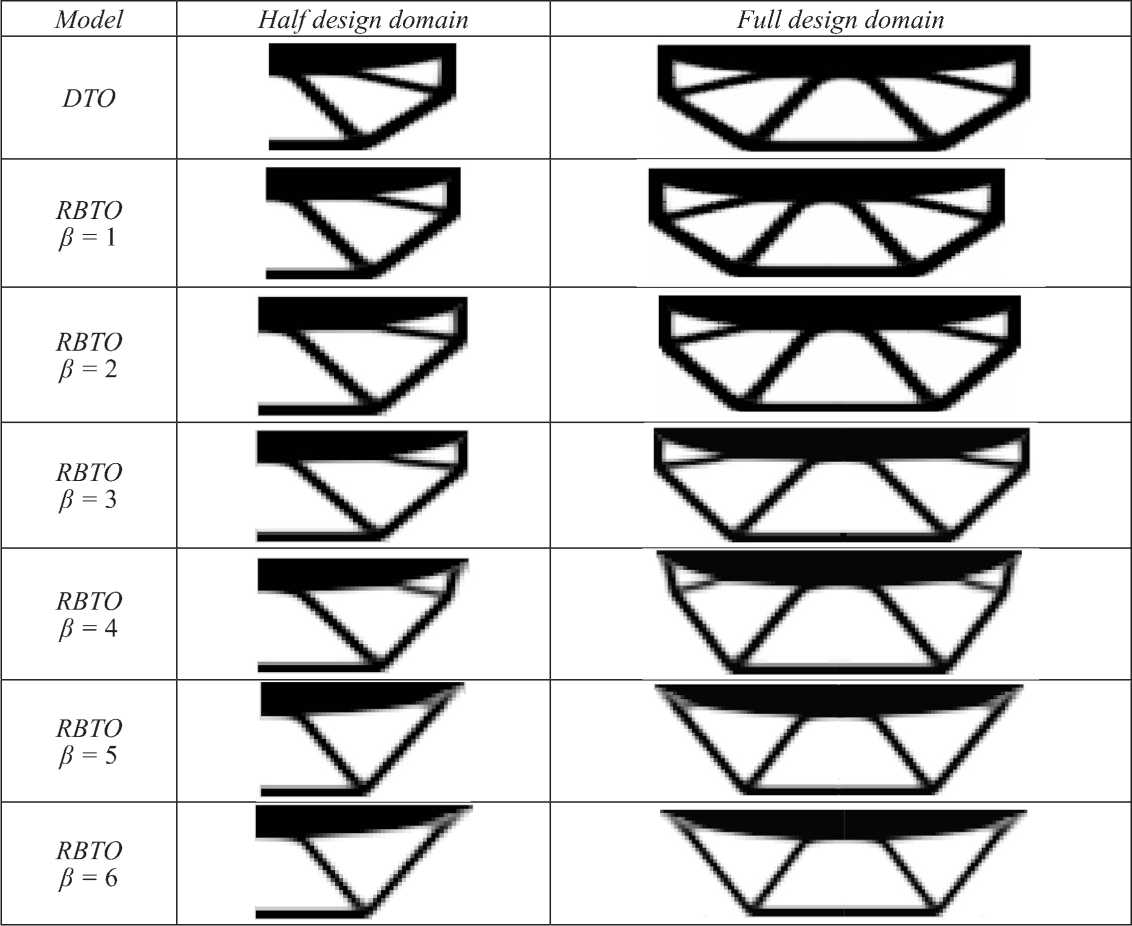
In order to demonstrate the effect of reliability index, we generate several topologies considering different reliability levels. The code is developed using MATLAB and based on the previous codes developed by the first author [5–7]. The objective is to perform topology optimization to obtain the best distribution of the materials. The topology optimization problem is then to minimize the compliance of the structure, subject to the volume fraction (50 %). The behavior of the used material is linear-elastic-isotropic. Table 1 shows the different resulting topologies for DTO layout and RBTO configurations for p e [ 1 - 6 ] .

ab

F i g. 1. Initial configuration and boundary conditions: a) full design domain; b) half of the design domain with symmetry boundary conditions

Р и с. 1. Начальная конфигурация и граничные условия: a) полная область проектирования; b) половина области проектирования с граничными условиями симметрии

T a b l e 1

Т а б л и ц а 1

Deterministic Topology Optimization (DTO) and Reliability-Based

Topology Optimization (RBTO) layouts

Детерминированная оптимизация топологии (DTO) и схемы оптимизации топологии на основе надежности (RBTO)

Shape optimization results

In order to demonstrate the importance of the integration of reliability constraints into the deterministic topology optimization, we apply a shape optimization algorithm to the different resulting topologies. The integration of the reliability-based method leads to different topologies relative to the positions of the elements making up the structure.

The shape optimization problem is to minimize the structural volume subject to mechanical stress using ANSYS Software. An MBB beam is loaded by a vertical pressure P = 20 N/mm². It is fixed at its up- 338

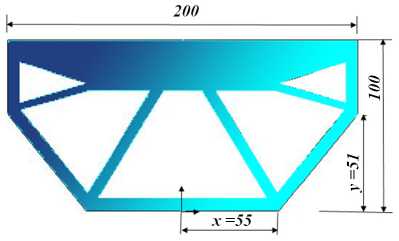
per extremities. The material in this beam is steel, which has a Young's modulus: E = 200 GPa and a Poisson’s ratio: v = 0.3. The allowable stress is σ_w = 970 Mpa. The beam length and height are: L = 200 mm and H = 100 mm, respectively and the thickness is considered to be: 20 mm.

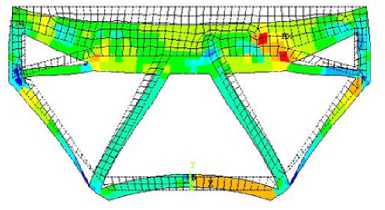
The resulting layouts are optimized considering three configurations. In figure 2a, the optimization variables are x and y . The first configuration corresponds to the DTO layout and RBTO layouts for β ϵ [1‒3]. For the resulting topology, the structural volume of the optimal configuration, illustrated in figure 2b, is 149000 mm³. figure 2b shows

Информатика, вычислительная техника и управление

the von-Mises stress distribution at the optimal configuration for the DTO layout and RBTO configurations when considering reliability indices: β ϵ [1‒3].

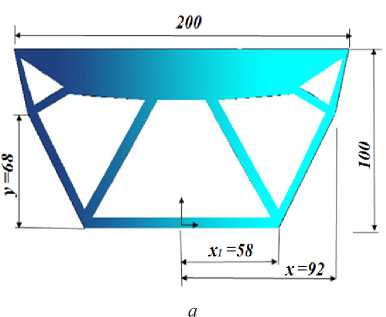
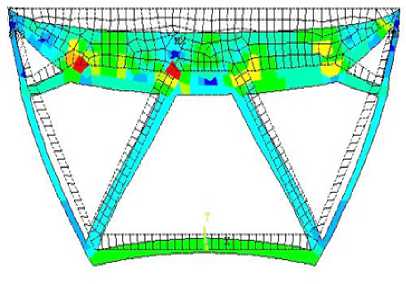
The second configuration corresponds to the RBTO result for β = 4. In figure 3a, the optimization variables are x , x₁ and y . For the resulting topology, the structural volume of the optimal configuration, illustrated in figure 3b, is 134100 mm³. Figure 3b shows the von-Mises stress distribution at the optimal configuration for the

RBTO configuration when considering reliability indices β = 4.

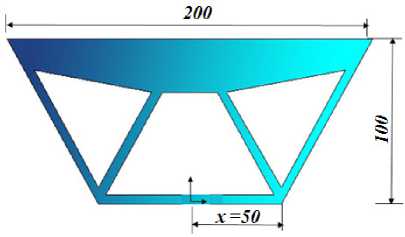
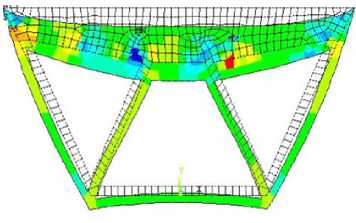
The third configuration corresponds to the RBTO results for β ϵ [5‒6]. In figure 4a the optimization variable is x . For the resulting topology, the structural volume of the optimal configuration, illustrated in figure 4b, is 132130 mm³. figure 4b shows the von-Mises stress distribution at the optimal configuration for the RBTO configuration when considering reliability indices β ϵ [5‒6].

a

b

F i g. 2. Deterministic Topology Optimization (DTO) layout and Reliability-Based Topology Optimization (RBTO) configuration when considering β = [ 1 ‒3 ] : a) geometrical model;

• b) von-Mises stress distribution

Р и с. 2. Детерминированная топология оптимизации (DTO): расположение и основанная на надежности топология оптимизация (RBTO) конфигурация при рассмотрении β = [1‒3]: а) геометрическая модель; б) распределение напряжений по Мизесу

b

F i g. 3. Reliability-Based Topology Optimization (RBTO) configuration when considering β = 4: a) geometrical model; b) von-Mises stress distribution

Р и с. 3. Конфигурация оптимизации топологии на основе надежности (RBTO) при рассмотрении β = 4: а) геометрическая модель; б) распределение напряжений по Мизесу.

a

b

F i g. 4. Reliability-Based Topology Optimization (RBTO) configuration when considering β = [5‒6]: a) geometrical model; b) von-Mises stress distribution

Р и с. 4. Конфигурация оптимизации топологии на основе надежности (RBTO) при рассмотрении β = [5‒6]: а) геометрическая модель; б) распределение напряжений по Мизесу

Discussion and Conclusion

The DTO algorithm leads to a single topology considering a given initial design space while the RBTO algorithm leads to several topologies relative to the reliability index values. Here, the reliability introduction on the topology optimization process leads to a significant change of layouts when the reliability index becomes more than 3.

To evaluate this effect, a shape optimization procedure is required. When the structural geometry evolves during the shape optimization process, the problem becomes more complex because the design variables are represented by coordinates of certain points in the geometry. The shape optimization loop contains three steps: 1) description of the geometry; 2) mesh and FEM evaluation of the model; 3) calculation of the gradients to minimize the ob- jective function. As result, we note that for the same boundary conditions, the RBTO second configuration reduces the structural weight by 10 %. The RBTO third configuration reduces the structural weight by 11 % for the same conditions.

Thus, reliability-based topology optimization is able to generate multiple topologies, giving the designer a range of solutions by adding certain reliability constraints. The proposed RBTO model aims to consider randomness (variability) of the most important quantities of a structure such as the geometry and the applied loads. This model can provide designers with several topologies. Another advantage is the reduction of weight of structures for the same conditions. This weight reduction will manifest itself in deterministic design optimization as well as in reliability-based design optimization.