The fractal model of nanocomposites polypropylene / carbon nanotubes melt viscosity

The inorganic nanofiller of various types usage for polymer nanocomposites production obtains widespreading at present [6]. However, the indicated nanomaterials melt properties are not studied fully enough. As a rule, when nanofillers application is considered, than compromise between improvement of mechanical properties in solid-phase state, melt viscosity enhancement at processing, nanofillers dispersion problem and process economic characteristics is achieved. Proceeding from this, the relation between nanofiller concentration and geometry and nanocomposites melt properties is an important aspect of polymer nanocomposites study. Therefore the purpose of the present paper is the study and theoretical description of the dependence of nanocomposites polypropylene/carbon nanotubes melt viscosity on nanofiller contents.

Experimental

Polypropylene (PP) “Kaplen” of mark 01 030 was used as matrix polymer. This PP mark has a melt flow index of 2.3-3.6 g/10 min, molecular weight of ~ (2-3) x 10⁵ and a polydispersity index of 4.5.

Carbon nanotubes (CNT) of mark “Taunite”, having an external diameter of 2070 nm, an internal diameter of 5-10 nm and length of 2 mcm and more, were used as nanofiller. They were prepared by chemical deposition (catalytic pyrolysis) of carbonhydrogens (CnHm) on catalysts (Ni/Mg) at atmospheric pressure and temperature of 853-923 K. CNT preparation process duration made up 10-80 min. In the studied nanocomposites taunite contents was changed within limits of 0.25-3.0 mass %.

Nanocomposites PP/taunite were prepared by components mixing in melt on twin screw extruder Thermo Haake, model Reomex RTW 25/ 42, production of German Federal Republic. Mixing was performed at temperature 463-503 K and screw speed of 50 rpm during 5 min. Testing samples were obtained by casting under pressure method on a casting machine Test Samples Molding Apparate RR/TS MP of firm Ray-Ran (Taiwan) at temperature 503 K and pressure 43 MPa.

The nanocomposites PP/CNT melt viscosity was characterized by a melt flow index (MFI). MFI measurements were performed on extrusion-type plastometer Noselab ATS A-MeP (Italy) with capillary diameter of 2.095 ± 0.005 mm at temperature 513 K and load 2.16 kg. The sample was maintained at the indicated temperature during 4.5 ± 0.5 min.

Uniaxial tension mechanical tests have been performed on the samples in the shape of twosided spade with sizes according to GOST 112 62-80. The tests have been conducted on universal testing apparatus Gotech Testing Machine CT-TCS 2000, production of German Federal Republic, at temperature 293 K and strain rate ~ 2 x 10^-3 s^-1.

Results and Discussion

For polymer microcomposites, i.e. composites with filler of micron sizes, two simple relationships between melt viscosity η , shear modulus G in solid-phase state filling volume degree ϕ _n were obtained [7]. The relationship between η and G has the following form:

П = G η 0 G 0 ,

where η ₀ and G ₀ are melt viscosity and shear modulus of matrix polymer, accordingly.

Besides, microcomposite melt viscosity increase can be estimated as follows (for ϕ _n <0.40) [7]:

η

- =^{1 +} Ф n .              (2)

η ₀

In fig. 1 the dependences of ratios η_n / η_m and G_n / G_m (where G_n and η_n are shear modulus and melt viscosity of nanocomposite, G_m and η_m are the same characteristics for the initial matrix polymer, accordingly) on CNT mass contents W_n for nanocomposites PP/CNT are adduced. The shear modulus G was calculated according to the following general relationship [1]:

E

^G = d; ■                (3)

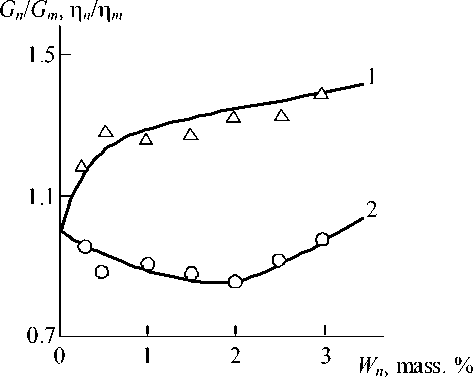
Fig. 1. The dependences of ratios of shear moduli G_n / G_m (1) and melt viscosities η _n / η _m (2) of nanocomposite G_n , η and matrix polymer G , η on nanofiller mass contents W for nanocomposites PP/CNT. n             mm                  n

where E is Young’s modulus, d_f is nanocomposite structure fractal dimension, determined according to the equation [1]:

d f = ( d - 1 )( 1 + v ) ,             (4)

where d is dimension of Euclidean space, in which a fractal is considered (it is obvious, in our case d = 3), n is Poisson’s ratio, estimated according to the mechanical tests results with the aid of the relationship [5]:

Q y = 1 - 2 v E “ 6(1 + v ) ,

where s _Y is yield stress, E is elasticity modulus.

MFI reciprocal value was accepted as melt viscosity η measure. The data of Fig. 1 have demonstrated clearly, that in the studied nanocomposites case the relationship (1) is not fulfilled both qualitatively and quantitatively: G_n / G_m increase corresponds to ratio η_n / η_m decay at W_n enhancement and absolute values η_n / η_m are lower essentially than the corresponding magnitudes G_n / G_m .

In Fig. 2 the comparison of parameters η_n / η_m and (1+ ϕ _n ) for nanocomposites PP/CNT is adduced. Discrepancy of experimental data and relationship (2) is obtained again: discrepancy of absolute values η_n / η_m and (1+ ϕ _n ) is observed and melt relative viscosity reduction corresponds to (1+ ϕ _n ) enhancement. At the plot of Fig. 2

drawing the value ϕ _n was determined according to the formula [8]:

W

Ф n = V,              (6)

ρn where ρ n is carbon nanotubes density, which was determined as follows [6]:

P n = 0 . 188 ( D CNT - D CN T ) ¹ / 3 , ⁽⁷⁾ where D _C ^ex _N ^t _T and D _C ⁱⁿ _N ^t _T are the mean magnitudes of external and internal diameters of nanotube, accordingly.

Hence, the data of Figs. 1 and 2 have shown that the fulfilled in polymer microcomposites case the relationships (1) and (2) are not correct for nanocomposites PP/CNT. In case of the relationship (1) correctness and Kerner’s equation application for shear modulus G calculation viscosity η_n lower boundary can be obtained according to the equation [7]:

П п = 1 + ² . 5 Ф n П т       ^{1 -} Ф n "

Since value η is inversely proportional to MFI, then in such treatment the equation (8) can be rewritten as follows:

n = nn. = MFIm = 1 + 2.5Фп re1   Пт   MFIn       1 - Фn ’

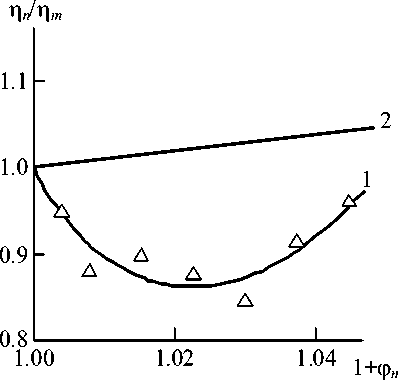
Fig. 2. The dependences of melt viscosities ratio of nanocomposite and matrix polymer η _n / η _m on nanofiller volume contents (1+ ϕ _n ) (1) for nanocomposites PP/CNT. The straight line shows the relation 1:1

where η_rel is nanocomposite melt relative viscosity, MFI _m and MFI _n are MFI values for matrix polymer and nanocomposite, accordingly.

In Fig. 3 the dependence of MFI _n on CNT mass contents W_n for nanocom-posites PP/CNT, calculated according to the equation (9), is adduced. As one can see, the quantitative discrepancy of theoretical calculation (curve 1) and experimental data (points) is observed. If the equation (9) assumes melt viscosity increase (MFI _n reduction) at Wn growth, then the experimental data find out opposite tendency (MFI _n > MFI _m ).

The indicated discrepancy requires principally distinguished approach application at polymer nanocomposites melt viscosity description. Such approach can be fractal analysis, within the frameworks of which the authors [4] proposed the following relationship for fractal liquid viscosity η estimation:

П ( l ) п 0 1 2 - d f ,                 (10)

where l is a flow characteristic linear scale, η ₀ is constant, d^'_f is fractal dimension.

As it is known [9], CNT in virtue of their strong anisotropy (in the taunite case the mean ratio of length to the diameter is more than 45) and low transverse stiffness form ring-like structures with radius RCNT, which can be determined with the aid of the equation [3]:

_ n ^CNT - CNT-

⁽ 2 ^R CNT )

where L _CNT and r _CNT are length and radius of carbon nanotubes, accordingly.

Further the radius R _CNT is accepted as l. Since CNT surface gets into contact with polymer then makes contact, then its fractal dimension d_surf was chosen as d^'_f . The value dsurf can be estimated as follows [6]. The value of CNT specific surface S_u was estimated according to the equation [2]:

V =   6

u ext ,                  (12)

ρn CNT and then the dimension dsurf was calculated with the aid of the equation [6]:

S u

= 410

I

ext D CNT

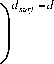
Calculation according to the equation (13) gives the value d_surf = 2.79. As it is known [1], polymer matrix macromolecular chain is not capable to “reproduce” CNT surface high roughness and therefore it “perceives” the indicated surface as much smoother. In this case one should use the effective value d ( d^ef ), surf surf which is equal to [10]:

^ef               .                (14)

surf            surf .

And as earlier, the value η in the equation (10) was considered as reci-procal value of MFI _n , and the constant η ₀ was accepted equal to 1.1 (MFI_m)^-1. At these conditions and replacement proportionality

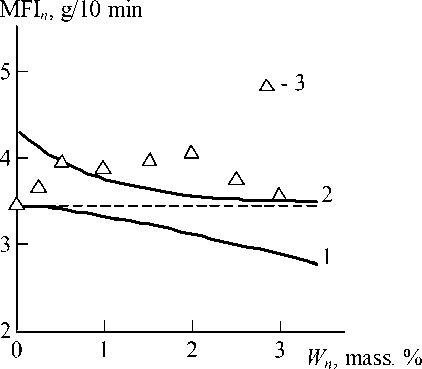
Fig. 3. The dependences of melt flow index MFI _n on nanofiller mass contents W_n for nanocomposites PP/CNT. 1 – calculation according to the equation (9); 2 – calculation according to the equation (10); 3 – the experimental data

sign in the relationship (10) by equality sign the theoretical MFI _n values can be calculated, if the value R _CNT is given in microns. In Fig. 3 the comparison of the obtained by the indicated mode MFI _n values and the experimental dependence MFI _n ( W_n ) is adduced, from which a good correspondence of theory and experiment follows.

The relationship (10) allows to make a number of conclusions. So, at the mentioned above conditions preservation R _CNT increase results to nanocomposite melt viscosity reduction. Enhancement d_surf , i.e. CNT surface roughness degree increase in virtue of the equation (14) usage, influences similarly. The indicated factors, critical ones for CNT, are not taken into consideration in the continuous treatment of melt viscosity for polymer microcomposites (the equation (8)).

Conclusions

Obtained in the present paper results have shown that the developed for microcomposites rheology description models do not give adequate treatment of melt viscosity for polymer nanocomposites filled with carbon nanotubes. The correct description the indicated nanocomposites rheological properties can be obtained within the frameworks of fractal model of viscous liquid flow. It is significant that such approach distinguishes principally from the used ones at microcomposites description. So, for nanocomposites filled with nanotubes the last rolling up degree in ring-like structures and their surface effective fractal dimension is necessary to take into consideration.