The Generation system of Textile Pattern draft Based on Quasi-regular Pattern Theory

Published Online October 2009 in MECS

There are a lot of stochastic web in nonlinear dynamic system. By the visualization of nonlinear science, people can see the inimitableness novel and beauteous graphics which formerly formed invisible field of dynamics. In which uniform stochastic web and quasi-regular patterns have unique balanced symmetry. With various fancy and beauteous structures they distribute on the whole space of dynamic system. And their compositions are mostly two-dimension continuity or quadrilateral continuity. Thus they are more suitable for manifested as textile patterns.

However the number of patterns just generated from hamiltonian is limited. In order to obtain more patterns it is necessary to carry out transformation and expansion of the hamiltonian.

Based on this idea, the paper adopt the method of superposed and nested other functions, taking the absolute value or opening radical sign, and setting the transformable parameters in hamiltion equation. It forms the evolvement model of the phase space, and increases the sorts and quantity. Finally it successfully achieves the purpose of obtained fine patterns.

As a powerful and excellent interactive tool Visual Basic is easy to develop simulation software under the

Manuscript received January 21, 2009; revised June 17, 2009; accepted July 23, 2009.

Windows platform. Therefore the system chooses Visual Basic to implement. The system provides features such as changing parameters, choosing functions and preparing colors. It can generate many fine and fashion patterns through flexible changing these setting. It shortens period of pattern design and has better practicability.

• II.    Mathematical model of quasi-regular patterns

Hamiltonian function of dynamic system is:

H = -a(x2 + y2) - Kcosy 25(t - j)

Where x , y were coordinate variables, K was interaction constant, a was rotation angle of twodimensional twist map, t was dimensionless time.

The differential equation of corresponding of Hamiltonian function on the above was as follows:

to y 2 ^( t - j)

j =-”

dx

= a y + K sin dt

dx dt

= -a y

Suppose q is positive integer, then the expression of frequent vibration twist of map q is:

xn+1 = (xn + K sin Уп ) cos(---) + Уп sin( qq

2n

Уп+1 = -(xn + K sin Уп )sin(---) + Уп cos( qq

When q = { 1,2,3,4,6 } is, phase space patterns were period meshes. And they have q times of rotational symmetry. When q = 5,7,8 l is, they can form various symmetric and complex quasi period meshes.

In order to get q times of rotational symmetry patterns, Hamiltonian function should perform smoothing processing. The concrete steps are: first it is transformed to a rotational coordinate system at a frequency of

• У = — ; then to seek average for time.

q

New Hamiltonian was produced by its operation of smoothing treatment, it is:

H Г) = Z cos( u cos -^П- + v sin — j ) (4) j =1               q            q

The Hamiltonian is intergrabel, described the conservative system of single degree of freedom. Of which the contour of energy surface H q ) is H q0 ( u , V ) = E . They give various shapes and sizes

curves family of closure invariant of H_q system. The

patterns, composed of these, is had q times of quasiregular patterns.

Bellow is the energy surface diagram of H ^ ) by drawing from Matlab, and the projection, that is contour line, in x , y plane. It Show as follow:

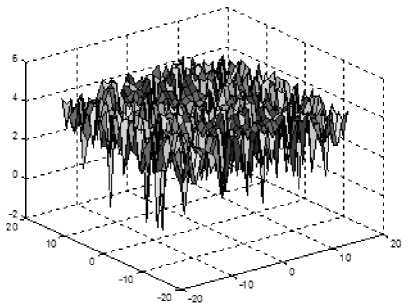
Figure 1.

«S* cP« 0^0 D°0 Ь°0 »% »Ъ*^; ’< cP J сРо оЧо D®0 o?o оЧз >% 1' ’-C^Wo®^ 3-C До°сЛп X^&cg,^»»;

/М^^Х^С,, ^.сГоо^о;^^^^ Й^^Я^.^.^^^

H (0) ^q

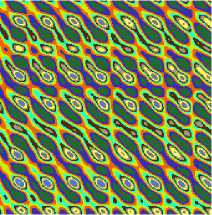
Figure 3. Quasi-regular pattern

Figure 2 shows the quasi-regular pattern consisted by formulas (4). The symmetry time of fig(a) is 4 , and the symmetry time of fig(b) is 6.

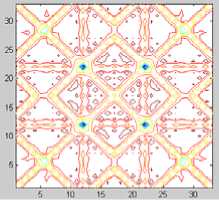
(a) 4 times

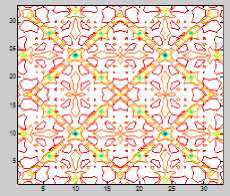
(b) 6 times

Quasi-regular pattern

Figure 2.

In which uniform stochastic web and quasi-regular patterns have unique balanced symmetry. With various fancy and beauteous structures they distribute on a whole space of dynamic system. And their compositions are mostly two-dimension continuity or quadrilateral continuity. Thus they are more suitable for manifested as textile patterns. The pattern shows in Figure 3.

Ш Mathematical Transformation for The

Hamiltonian

The pattern generated by formula (4) is limited in quantity and content. In order to get more patterns, we must expand and transform the function which is expressed by formula (4). Thus we adopt the method which is superposition, nesting and parameter variations on the existing function. They can form its evolution model in the phase space and increase the sorts and quantities. Finally it achieves the purpose of obtained fine patterns.

A. Superposition of function

For formula (4), let:

f ( x , y ) = h;« > =

q

Z

- = 1

^     2nj     . 2nj cosl x cos--+ y sin —

I q q )

= cos ( A + B )

And let:

g ( x , y ) = Z cos(cos( x ^{2 n j}- ) + sin( y ^{2 n j}- )). (6)

- = 1             q           q

After the formula (5) Superpose and formula (6), it has:

F ⁽ x , y ) = f ⁽ x , y ^{) +} g ⁽ x , y ) =

q

V cos x cos ^ j + y sin j^- + к q q J

V cos cos x ^j + sin y ~ ^j ll q J

j =1 ^q

j =1

2 П

Moreover ， For formula (4), let:

^q             2 n j , • 2 n j.

f ( u , v ) = nq^! = V cos( u cos     + V sin )

q    j = 1            q q

Let,

к

g ^{( u} , v ) = H ^ )

Comparing Figure 4(a) with Figure 4(b) which is generated by the formula (6) and (7), we can get the result that the pattern has the obvious variation after the function superposition.

q

= Vcos( j=1

2nj u cos

+ 1)

Then,

q

(a) Before the superposition (b) After the superposition Figure 4. Quasi-regular pattern

q

F (x, y) = V cos( u j=1

2 П . 2 П cos-- + v sin---

qq

q

+ V cos( j=1

2 n j u cos

q

+ 1))

Then they generate the Figure 6(a) and (b).

B. Nesting other functions

It is respectively to nest other new trigonometric function and exponential function in front of the

, 2П            2nj cos(x    ) and the sin( y ) , or it is to nest the one qq of them. The example is:

(a)

Figure 6. Quasi-regular pattern

(b)

hl( x, y) = V cos(cos( x —L) + sin(tan( y —L)))

j=1            qq h2 (x, y) = V cos(exp( cos(x 2П-)) + exp(sin(y 2nj-))) (9) j=1                 qq

The Figure5 (a) and (b) shows the patterns which are generated by the formula (8) and (9).

(a) Nested trigonometric one (b) Nested exponential one Figure 5. Quasi-regular pattern

The Figure 5(a) and (b) show that patterns which are transformed by the functions are different on structure and style.

C. Using absolute value or radical sign

It is respectively to use absolute value or radical sign

2nj             2t-x     „ . , on the cos(x    ) and sin( y ) , or it is to use one qq of them.

h 2 ( x , y ) = V cos(cos( abs ( x ^j)- )) + sin( abs ( y ^j^- )))

j = 1                q                q (10)

h з ( x , y ) = V cos( sqr (cos( x ^^п-- )) + sin( y ^^nj- )) j = 1                q            q

Then they generate the Figure 7(a) and (b).

(a) Used absolute value (b) Used radical sign

Figure 7. Quasi-regular pattern

D. Parameter variations

Example of a Parameter variations is given:

f ( x , y ) = H^ =

q

^cos( x j=1

2nj      . 2nj, cos—- + y Sin—-) +

qq

q

^ cos ( tan(sin x cos y )

j = 1

For formula (12), When the symmetrical number of times is 5 , obtains Figure8 ( a ) , We change the symmetrical number of times 9, then obtains Figure 7 (b).

(a) times is 5      (b) times is 9

Figure 8. Quasi-regular pattern

We add coefficient k into the formulas which are transformed by mathematical method from formula (5) to (11). We can get a large number of different patterns by using different value of k. Figure 9 is the pattern which is generated by the same function but with the different parameters.

Figure 9. Patterns generated by the same function but with the different parameters.

Therefore we get a 110 of functions by these variation methods. In these function we can choose favorite patterns for textile fabric design pattern.

W Production of gallery

By the research on quasi-regular patterns mathematical model Evolution Mechanism, from which some parameters were extracted as follow: Choice Function, respectively, it means that choose a function from function databases which has 1~110 functions; Symmetric times, its value is commonly in 4~12 and pixel value is in 256~800. Galleries, which will be used for textile designers, were built based on quasi-regular patterns gallery by configuration parameters to automatically generation of a lot of patterns elements.

Color matching can be chosen again at satisfactory patterns, the method can be both random color matching and latest fashion color matching. Meanwhile , it also adopts several different color series to do color matching, enriching its color for the chromatically feature in textile, for a certain pattern.

Figure 10 shows the effect of the pattern which is created by the same function, different parameter and color matching.

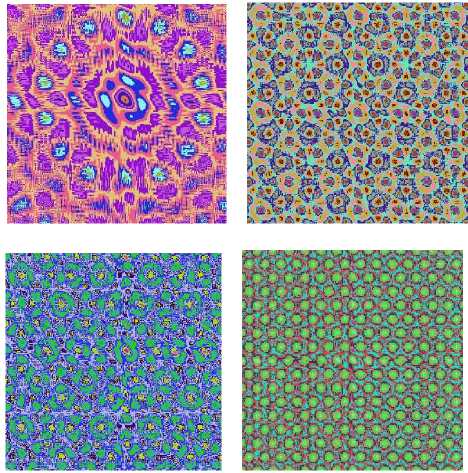
Figure 10. Table of the same function, different parameter and color matching

V Textile patterns generation system

As a powerful and excellent interactive tool Visual Basic is easy to develop simulation software under the Windows platform. Therefore the system chooses Visual

Basic to implement. The system provides features such as changing parameters, choosing functions and preparing colors. It can generate many fine and fashion patterns through flexible changing these setting. It shortens period of pattern design and has better practicability.

Main interface of textile patterns generation system shows in Figure 11 as following.

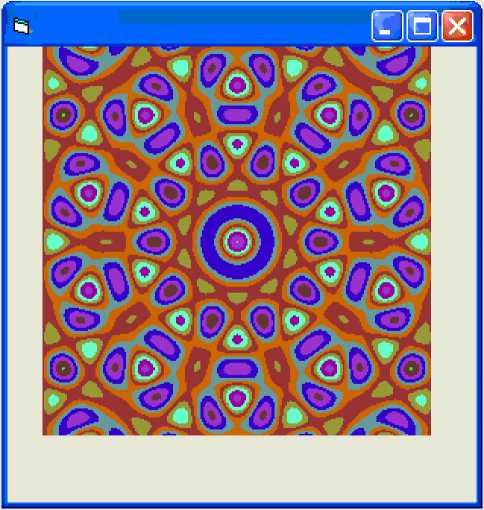
Figure 13. The generated quasi-regular pattern

Figure 11. Main interface of quasi-regular patterns

Above the interface there is a toolbar in which have six |Г"Ь| и . It means to can make a

. It means to save the current pattern. Forth one is “parameter set”, means setting of parameters. A setting interface will pop up when the key is clicked. It contains four settings: trim size, symmetry time, canvas size and function number, as in Figure 12. It automatically generates a pattern after all the setting is done, as in Figure13.

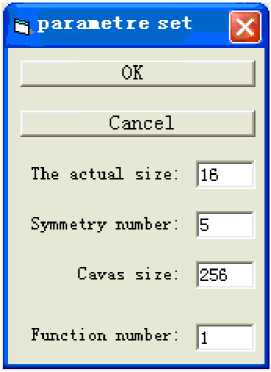
Figure 12. The setting interface of parameter

In the function key “parameter set” trim size shows actual size of pattern and values range from 8 to 32. The values of function number range from 1 to 110.

A function is called to plot quasi-regular pattern. The trim size is set to 16, and the canvas size is set to 256. With the preservation of the two values the symmetry time is set to 6, 8 and 9 orderly. Then patterns are generated as in Figure 14. The called function is:

h = h + Cos(X * Cos(2 * pi * i / q)

+ Y * Sin(2 * pi * i / q)).

^®^C- 8 • ^5 ООО 63(0 6

‘$ °. ° о ° ,8

» fe ® В О)О @ « (

D     О     О     О     С ооо |КЗ(о к з     о     о     •     с

0    0    0    0

ЙВ • 8 ° 8 ' ЭЙ

(a) Pattern of 6 times symmetry

(b) Pattern of 8 times symmetry

(c) Pattern of 9 times symmetry

Figure 14. The generated patterns

The fifth function key is “automatic demonstration”. A series of fine quasi-regular patterns are generated after clicked this key. In auto-displaying the numbers of quasiregular patterns are limited in 110. function transformation

According to numbers of the different groups are displayed in the following

The trim size is set to 16 and the canvas size is set to 256, and keep them unchanged, changed the symmetry time to 5 、 7 、 and 10, changed the function number to 250 、 46 and 59, Generated patterns show as in Figure 16

To compare with the pattern in Figure 10 it will be found that patterns of odd symmetry all have comparability in some extent, and the same to even symmetry.

In the following three continuous odd numbers are chose to draw patterns in one called function. The trim size is set to 16. The canvas size is set to 256. And the function number is 3. With the preservation of the three values the symmetry time is set to 5, 7 and 9 orderly. Generated patterns show as in Figure 15. The called function is:

h = h + Cos(X * Cos(2 * pi * i / q) + Y * Sin(2 * pi * i / q)) + Cos(Exp((-Abs(Sin(Y) * Cos(X)))))

(a) Pattern of 5 times symmetry

(b) Pattern of 7 times symmetry

(c) Pattern of 9 times symmetry

Figure 15. The generated patterns

Figure 16. The generated patterns of a group

To compare with the three quasi-regular patterns it will be found that the trim size and canvas size are unchanged, and changing the symmetry time and function number will produce the patterns very comparable pattern of structural.

The patterns of the first, second and third groups shown in Figure 17, to compare with the three patterns, we will find that has some comparability of symmetry and structural.

Figure 17. The generated patterns of different group

The sixth function key is “automatic save”. Inquiry interface in Figure 18 is generated after clicked this key. The Interface in the storage path interface in Figure 19 is generated after clicked the “OK” in inquiry interface, and you need to key in the path name of the picture storage. In Figure19, we will find the “picture 1” which we stored in the folder of f disk after clicked the “OK”. There is another interface (in Figure 20) named interface of autosave function after the interface in the storage path. As shown we key 10, and we storage 10 groups quasi-regular patterns based on different function combinations and transformations.

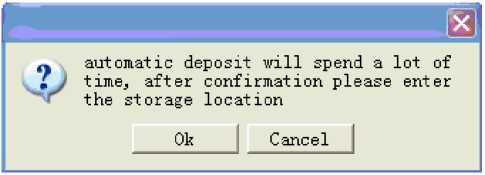
Figure 18. Inquiry interface

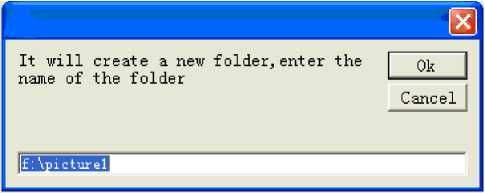
Figure 19. The storage path interface.

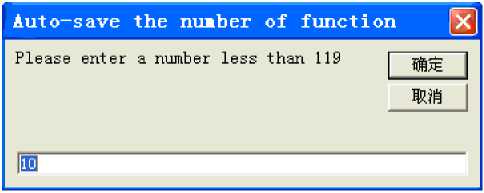
Figure 20. Interface of auto-save function

4 Conclusion

The most of quasi-regular patterns generated by hamiltonian have balance and symmetry. They are very suited to present the textile pattern design. However the number of the patterns has limited in number and sorts. By using the methods of superposition, nesting, combination and parameters variations on hamiltonian we built a 110 of functions. All of these functions can generate fine patterns suited for textile fabric design.

The system of textile pattern draft is generated by Visual basics for the computer. The system provides features such as changing parameters, choosing functions and preparing colors. It can generate many fine and fashion patterns through flexible changing these setting. It shortens period of pattern design and has better practicability.

The method in this paper has overcome the limitations of traditional hand-drawn pattern. And it also shortened the cycle of design pattern. There will be a good prospect of application in textile design.