The influence of astigmatic aberration on the Gaussian beam diffraction in the near field of axicons and ring gratings

It is well known that a real lens always introduces distortions when forming an image [1 – 3]. One of the causes of distortions are various types of aberrations, such as coma, distortion, astigmatism, and others [1, 2]. Reduction and compensation of optical aberrations is an urgent problem solved by adaptive optics [1, 4 – 6], the use of which allows obtaining high–quality images of biological structures in complex tissues and medical diagnostics [3, 6 – 8], images of exoplanets in astronomy [1, 9], compensating for chromatic aberrations [10], including in the development of virtual reality headsets [11], contact lenses [12]. It is known to use methods based on artificial intelligence for detection, compensation and recognition[13 – 18], in particular, to compensate for phase aberrations in digital holography [16, 18]. It should also be noted that a number of defects of optical systems could be described by wavefront aberrations [19 – 21].

Diffractive optical elements (DOE) [22 – 29] are distinguished by their versatility and efficiency when used in such areas as optical communications, holography, formation of the required distribution of laser beams, visualization systems, and compensation for aberrations of optical systems [22]. Formation of a complex spatial distribution during generation of the second harmonic of a Bessel–Gauss beam by axicons with asymmetric aberrations is known [23]. It should also be noted that in the case of subwavelength dimensions of elements, it is important to take into account the height of individual relief elements [26, 29, 30].

Gaussian beams have not lost their relevance to this day when solving problems in photonics and optics [30 – 42], in particular, when forming long optical needles [35, 36] and optical bottles [26, 30], sharp focusing [33, 36], and other areas of optics [38]. There are also known works on the propagation of Gaussian beams in various media, in particular, under conditions of anisotropic turbulence [31].

The propagation features of Gaussian beams with introduced astigmatic aberration on ring gratings at different relief heights examines in this paper. Numerical modeling was performed using the finite difference time domain (FDTD) method [43] using software Meep [44 – 46].

1.    The simulation parameters and input beams

The following simulation parameters were used in the paper: the input radiation wavelength λ = 0.532 μm. A three– dimensional computational domain was considered, where x , y , z ∈ [0, 15.8λ]. This domain was surrounded by an absorbing layer PML (1.1λ) on all sides. The spatial simulation step was λ/50, the time simulation step was λ/(100c), where c is the speed of light. The fundamental Gaussian mode (beam size σ = 1.5 μm) with circular polarization was considered as the input beam, supplemented with an astigmatic aberration of the form exp ( i α xy / R ²), where R – is the radius of the considered domain, α is a parameter corresponding to the value of aberration. Examples of input beams propagating in free space outside the element are shown in Fig. 1 (α =0, 35.99, 71.98, 107.98, 141.68).

The diffractive axicons and ring gratings with numerical aperture NA = 0.95 and refractive index n= 1.47 were considered as an optical elements, where NA = λ / d ( d – period of the axicon and the ring grating, d = 1.05λ).

The relief heights of this elements h corresponded to a phase jump of n radians ( h = 1.06k), as well as multiples of this value: 2n ( h = 2.12k), 3n ( h = 3.18^) and 4n ( h = 4.24k) radians. A study was also conducted on the passage of the considered laser beams through axicons with a similar height, but without a central zone.

Fig. 1. The input beams, at different values of a, intensity: a) a = 0, b) a = 35.99, c) a = 71.98, d) a = 107.98, e) a = 141.68

The diffraction patterns of the Gaussian beam propagation (a = 0) through the diffraction axicons are shown in Fig. 2 (with a central zone) and Fig. 3 (without a central zone)

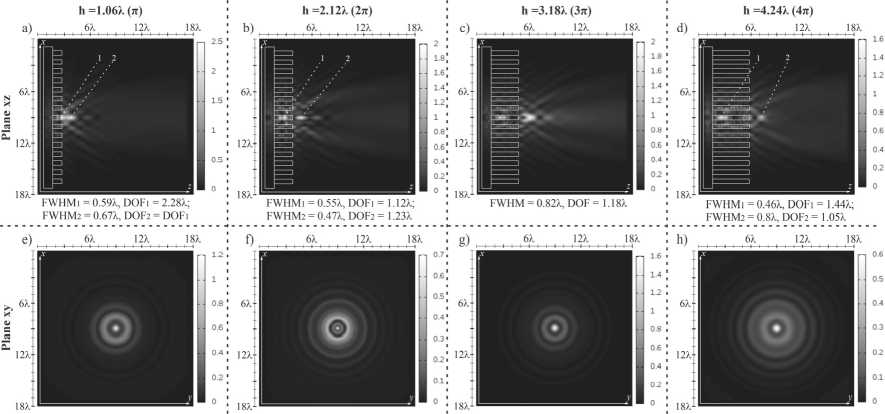
Fig. 2. Two-dimensional diffraction pattern (intensity) of a standard Gaussian beam (a = 0) at different axicon relief heights, xz plane (a, b, c, d) and in the xy plane at a distance S = 1.5k (e,f g, h)

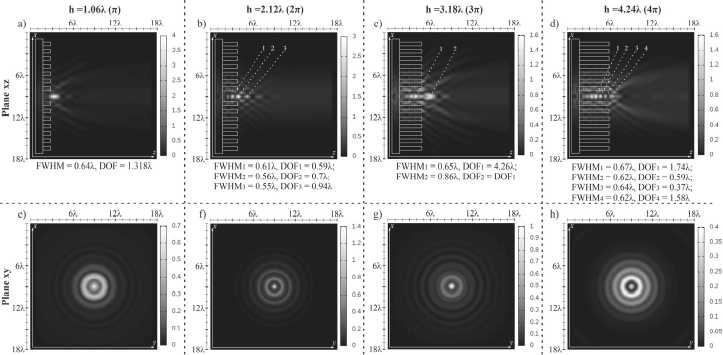
Fig. 3. Two-dimensional diffraction pattern (intensity) of a standard Gaussian beam (a = 0) at different relief heights of the axicon without a central zone, in the xz plane (a, b, c, d) and in the xy plane (e, f, g, h), the sections in the xy plane were considered at a distance S = 1.5k

The focal spot size in the transverse region was estimated as the full width at half maximum (FWHM) intensity, in the longitudinal region the light needle size was estimated similarly (depth of focus, DOF). The values are given for the global maximum on the optical axis and the maximum outside the element. In the case of several maxima, their locations are indicated by numbers in the figures. Transverse diffraction patterns (xy plane) were considered at the same distance from the edge of the relief of the elements S = 1.5k in all cases considered in the paper.

The following should be noted with analyzing Fig. 2: only for the case of h = 3.18k there is the formation of the main maximum outside the relief of the element observed at a distance of S = 1.2k. In the other cases, the main maxima are formed inside the element, although for the case of h = 1.06λ this occurs, in fact, at the boundary, at a distance of 0.07λ from the edge of the relief (Fig. 2a). It should also be noted that outside the relief in all the cases, a decrease in the intensity of the second maximum (outside the relief) of the element is observed.

Let I – be the intensity value from the maximum value on the optical axis, which is 100 %. Then, at h = 1.06λ, the maximum outside the element is I = 97.73 %, at h = 2.12λ, for the maximum outside the element, I = 87.6 %, and for h = 4.24λ, the maximum outside the element is I = 71.9 %. The minimum focal spot size outside the element was obtained for the case h = 2.12λ (FWHM = 0.47λ), the maximum light needle – for the case h = 1.06λ (DOF = 2.28λ).

If we remove the central zone, the maximum will be formed outside the element. For the height h = 1.06λ, one main maximum is observed on the optical axis in contrast to the previously considered case. A further increase in the relief height leads to the formation of a chain of foci on the optical axis, which is especially noticeable for the case of h = 4.26λ. We will separately note the case of h = 3.18λ, when the formation of a light needle with a length of DOF = 4.26λ is observed.

2.    The Gaussian beam with astigmatic aberration and ring gratings height changing

This section considers the cases when α = 35.99, 71.98, 107.98, 141.68. The diffraction patterns for the propagation of Gaussian beams with astigmatic aberration through the previously considered diffraction axicons are shown in Fig. 4.

Fig. 4. Two–dimensional diffraction pattern (intensity, xz plane) of Gaussian beams for different values of α (35.99, 71.98, 107.98,

141.68) at the height of the ring grating h = 1.06λ (a, e, i, m), h = 2.12λ (b, f, j, n), h = 3.18λ (c, g, k, o), h = 4.24λ (d, h, l, p)

It should be noted that the main maxima are formed inside the element as before, only for the case of h = 3.18λ at α = 141.68 (Fig. 4 o ) the formation of the main maximum is observed outside the ring grating with FWHM = 0.73λ and DOF = 2.27λ.

The main maximum is formed inside the relief for the height h = 1.06Z on the boundary, within 0.07^ for the cases a =35.99, 71.98, 141.68, but for the case a = 107.98, the main maximum is formed already at a distance of 0.42Z.

The intensity value of the maxima on the optical axis is generally significantly smaller in contrast to the case of a standard Gaussian beam without distortions: in half of the cases considered in Fig. 4, I < 70 %. Only in two cases is observed I >90 % , at h = 3.18Z and a = 35.99 ( I =91.2 %, Fig. 4 c ), and at h = 4.26^ and a = 107.98 ( I =90.9 %, Fig. 4 1 ). However, for all considered a in the case of height h = 4.26Z, the value of the maximum outside the element is I > 70%.

The minimum focal spot size outside the element was obtained for the case of h = 2.12^, a = 35.99 (FWHM = 0.52Z, I =56.7%, Fig. 4 b ), light needles larger than 5Z were obtained for the cases of h = 1.06Z, a =141.68 (DOF = 5.96Z, I = 29.6%, Fig. 4 m ); h = 1.06^, a = 71.98 (DOF = 5.54Z, I =57.8%, Fig. 4 e ); and h = 3.18Z, a = 71.98 (dOF = 5.23Z, I = 68.4 %, Fig. 4 g ).

However, the longitudinal section does not provide complete information about the diffraction patterns formed. Let us also consider the cross sections, as before, at a distance of 1.5Z (Fig. 5).

Fig. 5. The sections in the xyplane (intensity) at a distance S = 1.5 Z , with a = 35.99 (a, b, c, d), a = 71.98 (e, f, g, h), a = 107.98 (i, j, k, l), a = 141.68 (m, n, o, p)

It should be noted that for the case of h = 3.18Z (for all considered a) the formation of a light spot is observed on the optical axis, and for a =141.68 it is the least distorted.

A focal spot of comparable size is also observed for the case of h = 4.26Z and a = 107.98.

3.    The Gaussian beam with astigmatic aberration and ring gratings height changing without the central zone

It was shown earlier that the main maxima are mainly formed inside the optical element. As before, we will change the height of the elements, but without the central zone.

The obtained intensity distributions during the propagation of Gaussian beams with astigmatic aberration through ring grating without a central zone are shown in Fig. 6, and the transverse intensity distribution patterns in the xy plane at a distance of S = 1.5Z are shown in Fig. 7.

In all cases, the main maximum is formed outside the relief of the axicons, and also outside the height of the relief of the element rings.

For the height h = 1.06Z one main maximum is observed on the optical axis as for the Gaussian beam at a = 0, in contrast to the two maxima of the previous section at a similar element height. Increasing the height of the element rings leads to the formation of chains of foci on the optical axis. For the case of a =71.98 at a height of h = 2.12Z (Fig. 6 f), the formation of two optical bottles is observed.

The minimum focal spot size was obtained for the case of h = 4.24Z, a =141.68 (FWHM = 0.43Z, I = 100 %, Fig. 6 p ), and light needles larger than 4 Z were observed for the cases of h = 3.18Z, a = 71.8 (DOF = 5.01Z, I =71.1 %, Fig. 6 g ), h = 1.06Z, a =107.98 (DOF = 4.86Z, I =100%, Fig. 6 i ) and h = 2.12Z, a = 71.98 (DOF = 4.44Z, I =73.2%, Fig. 6 f).

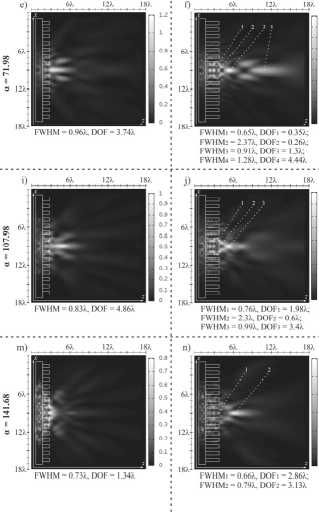
Fig. 6. Two–dimensional diffraction pattern (intensity, xz plane) of Gaussian beams at different values of α (35.99, 71.98, 107.98, 141.68) at the height of the ring grating without the central zone h = 1.06 λ (a, e, i, m), h = 2.12λ (b, f, j, n), h = 3.18 λ (c, g, k, o) and h = 4.24 λ (d, h, l, p)

Fig. 7. The sections in the xy plane (intensity) at a distance S = 1.5 λ , with α = 35.99 (a, b, c, d), α = 71.98 (e, f, g, h), α = 107.98 (i, j, k, l), α = 141.68 (m, n, o, p), ring grating without central zone)

It should be noted that the formation of more extended light needles was observed when using elements without a central zone than in its presence for all types of beams. Despite the smaller dimensions of the light segments on the optical axis, the intensity values were generally higher than in the presence of a central zone in the subwave axicon.

Conclusion

The FDTD method was used to study the diffraction of Gaussian beams with astigmatic aberration under circular polarization on diffraction axicons with and without a central zone for different relief heights of elements in this paper. The relief heights of the elements were chosen as multiples of the phase jump of n radians. It was shown that an increase in the relief height leads to the formation of chains of maxima outside the element.

The minimum focal spot size of Gaussian beam without aberrations was obtained for the case of h 2.12л (FWHM = 0.47Л), the maximum light needle - for the case of h = 1.06Л (DOF = 2.28Л).

The minimum focal spot size outside the element in the presence of astigmatic aberration was observed for the case of an axicon without a central zone for h = 4.24Л, a = 141.68 (FWHM = 0.43X), the longest light needle (in the presence of astigmatic aberration) was obtained for the case of h = 1.06Л, a =141.68 (DOF 5.96л).

Acknowledgements

This research was funded by the Russian Science Foundation under grant No. 24–79–10101, –79–10101/ (numerical simulation) and within the government project of the National Research Center "Kurchatov Institute" (the part Introduction).