The influence of molecular structure on the properties of poly (ethylene terephthalate) / poly (butylene terephthalate) blends

DOI:

Results and Discussion

According to the known Academician Kargin postulate [5], polymer properties are encoded on molecular level and are realized on supramolecular (suprasegmental) one. For poly(ethylene terephthalate)/poly(butylene terephthalate) (PET/PBT) blends, processed by two different methods, the essential distinction of their properties was found [12]. So, the impact toughness of blends PET/PBT, processed by extrusion and subsequent injection molding, is on the average 3.5 times larger of this characteristic for the same blends, processed by injection molding only. The purpose of the present work is the study of this effect on both molecular and supramolecular levels.

Experimental

Commercial engineering grade polymers: PET (9921W-Eastman Chemicals) and PBT (Vestodur X7085-Degusa Huls AG) were used in the research. Two types of blends were prepared: one by injection moulding using Engel machine ES 80/20HLS with the screw length/diameter ratio L / D = 18 and D = 22 mm and the second mixed at first by extrusion moulding machine Fairex with L / D = 24 and D = 25 mm and then injected on Engel machine. The processing temperature has been in the range from 498 K to 528 K for injection molding and in the range from 453 K to 513 K for extrusion at pressure of 90 and 30 MPa, respectively. The following PET/PBT were prepared: 100/0; 95/5; 90/10; 80/20; 70/30; 50/ 50; 25/75; 0/100 wt [12].

Charpy’s impact toughness has been measured on impact hammer INSTRON-PWS and Brinell microhardness on the hardness equipment HPK8206 and uniaxial tension tests have been performed on INSTRON-1115 testing machine [12].

As it is known [3], the mean-square distance between macromolecule ends á h ² ñ is given by the following relationship:

h h ^ ~ MM ^1+E,

where MM is polymer molecular weight, e is interaction parameter.

Within the frameworks of fractal analysis the parameter e is defined with the aid of the equation [8]:

D f = A, £ + 1

where D_f is fractal dimension of macromolecular coil, which in case of linear polymers can be estimated as follows [9]:

2 d

^Df " ^ ,

where d_f is a polymer structure fractal dimension, which is determined with the aid of the equation [8]:

H B σ _Y

0.07 + 0.6 lnl---f- l3 - df.

where H_B is Brinell microhardness, s _Y is yield stress.

The parameter e characterizes an interaction type of macromolecular coils in polymer blend: at e = 0 interaction of attraction and repulsion are balancing ones, at positive e repulsion interactions are dominant, at negative e are attraction ones [9].

The impact toughness A _p of polymer specimens without a notch is defined by two factors: the deformation energy release critical rate G _I , characterizing specimen plasticity, and the length of critical structural defect a _cr , initiating fracture process [9]. The value G _I is determined according to the equation [10]:

C, = 0.24 + 1.10( d - d_f ), kJ/m²,         (5)

c where d is dimension of Euclidean space, in which a fractal is considered (it is obvious, that in our case d = 3).

In Fig. 1 the dependence of interaction parameter e on the concentration of PBT C _PBT for the considered blends PET/PBT is adduced. This plot has two features. Firstly, it is a mirror reflection of the dependence of the considered blends impact toughness on their composition, adduced in work [12], and secondly, all values e are positive, i.e. the repulsion interactions are dominant for all considered blends. The indicated mirror reflection of the parameters A _p and e supposes A _p growth at e reduction, i. e. repulsion interaction weakness.

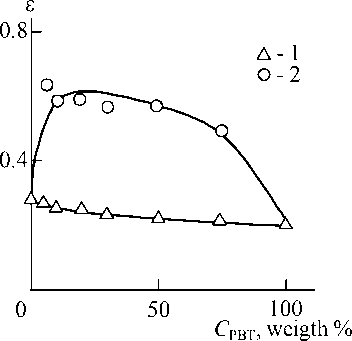
Fig. 1. The dependences of interaction parameter e on PBT content C _PBT for blends PET/PBT, prepared by extrusion and subsequent injection moulding ( 1 ) and injection moulding only ( 2 )

In Fig. 2 the dependence of deformation energy release critical rate G _I , calculated according to the equation (5), on the parameter e value is adduced for the considered blends PET/ PBT, which demonstrates linear G _I growth at e increasing. Such look of the dependence G _I ( e ) was expected, since repulsion interactions intensification enhances molecular mobility, that always results in polymers plasticity enhancement [6]. The correlation G _I ( e ) can be described analytically by the following empirical equation:

G_I= = 1.56(6 + 0.33), kJ/m². (6)

The equation (6) allows to determine limiting values G_I for the considered blends. At e = – 0.33 (the greatest attraction interaction) minimum value

G _I is equal to zero and at e = 1.0 (the greatest repulsion interaction) the maximum value G_I is equal to 2.07 kJ/m².

The length of critical structural defect a _cr can be determined with the aid of the following equation [9]:

A = GL p 72acr,

where L is distance between impact hammer supports (span).

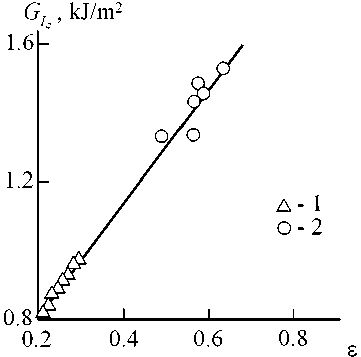
Fig. 2. The dependence of deformation energy release critical rate G _I on interaction parameter e for blends PET/PBT. Designations are the same, that in Fig. 1

In Fig. 3 the dependence of the length of critical structural defect a _cr on interaction parameter e for blends PET/PBT is adduced. The linear a _cr growth at e increasing is observed, that can be described analytically as follows:

a cr = 560(e - 0.20), mcm .           (8)

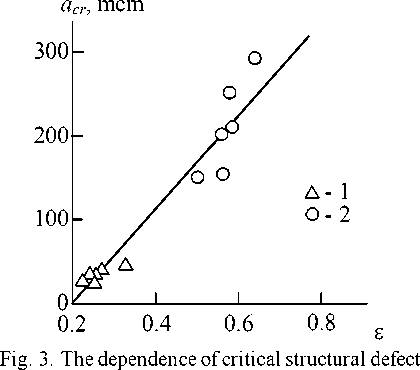
length a_cr on interaction parameter e for blends

PET/PBT. Designations are the same, that in Fig. 1

Let us consider the limiting a _cr values. At e = 0.20 the value a cr is equal to zero. The indicated condition e = 0.20 according to the equation (2) corresponds to D _f = 1.667 and according to the equation (3) – d _f = 2.5. As it is known [1], the criterion d f >  2.5 means the transition from brittle fracture to quasibrittle (quasitough) one, where the main role plays not a _cr value, but local (macroscopic) plastic deformation mechanisms. The greatest value a _cr at maximum repulsion interaction, i.e. e = 1.0, is equal to 448 mcm.

The equations (2) and (3) combination allows to obtain the following relationship between basic structural characteristic d _f and molecular parameter e , which is true for the linear polymers:

d, =---- ^f 1 + E

.

Thus, the equations (6)-(9) suppose the correlation between A _p and d _f . This supposition is confirmed by Fig. 4 plot, where the dependence A _p ( d _f ) for the considered PET/PBT blends is adduced. This dependence shows linear A _p growth at d _f increasing and the equations (6)-(8) combination allows to obtain the following relationship:

e + 0.33

e - 0.20^.

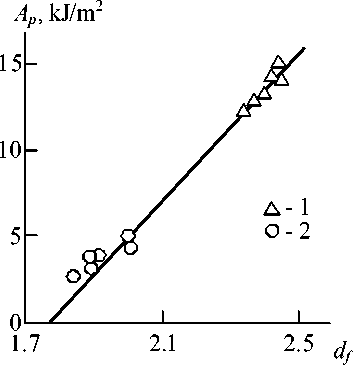
Fig. 4. The dependence of impact toughness A_p on structure fractal dimension d_f for blends PET/PBT.

Designations are the same, that in Fig. 1

From the relationship (10) it follows, that minimum value A p = 0 is realized at e = -0.33, i.e. the greatest attraction interaction or at polymer blend zero plasticity, that was to be expected (see

the equation (7)). The greatest value A p > * is realized at e = 0.20 or df. = 2.5. From the practical point of view the condition A_p ^* means the transition from brittle to tough fracture [1].

Conclusions

Thus, the present work results have confirmed the stated above Academician Kargin postulate. The impact toughness A _p of PET/PBT blends is controlled by macromolecular coils interactions, which on molecular level are reflected by structure fractal dimension. It has been shown that interaction parameter e controls the transition to both absolutely brittle ( A _p = 0, e = -0.33) and to tough ( A_p > * , e = 0.20) fracture.

Acknowledgements

The work is performed within the complex project on creation of hi-tech production with the participation of the Russian higher educational institution, the Contract of Tanneta JSC with the Ministry of Education and Science of the Russian Federation of February 12, 2013 No. 02.G25.31.0008 (Resolution of the Government of the Russian Federation No. 218).