The method for lifetime estimation through the mechanical properties in tension

For many years attempts have been made to understand the crack growth mechanism and predict lifetime under conditions of cyclic loading. Cracks exist in many structural components. The crack growth resistance is an important property of the material which controls the lifetime of the component. Studies on the growth of cracks have led to the observation that fatigue life of many engineering materials is primarily dependent on micro-structural features, such as inclusion particles, voids, slip-bands or manufacturing defects. Thus, knowledge of the crack rate makes possible the prediction of residual lifetime of a component. Due to that cracked component may be kept in service for an extended useful time. Applying the fracture mechanics principles makes possible to predict the number of cycles spent for crack growth to some specified length or to final failure.

Determining the critical cyclic loading conditions is commonly performed by using a Paris’ curve. The Paris’ curve is dependence of crack growth rate, da/dN on the stress intensity range ^A K = ^K m _a x ^- K min .

This curve may be divided into three regions (fig. 1). At low stress intensities, Region I, cracking behavior is associated with threshold, AKth, effects. By considering the term AKth the designer can ensure that no crack growth will occur. AKth is the “fatigue crack growth threshold”, and signifies the critical value of AK below which crack growth will not occur. It is calculated using the Paris’ curve, and is the value of AK corresponding to da/dN = 0. In the Region III, at high AK values, crack growth rates are extremely high and little fatigue life is involved. Finally, in the mid-region, Region II, the curve is essentially linear and can be described by the Paris’ equation da I dN = C (A K) n, (1)

where C and n are material constants and A K is the stress intensity: A K = K max - K_min.

However, the procedure for Paris’ curve determination by means of direct testing is enough complicated and expensive. Sometimes, it is just impossible, for example in cases when structures or equipment are under exploitation conditions.

Therefore many investigators made large efforts to develop models for Paris’ curve shape predicting. The relationship between fracture toughness, AK fc and K Ic , AK fc and K Id was shown in paper [4; 6]. The correlation between constants С and n in the Paris’ equation is known [3; 7]. But up to date there is no model for AK th and constants n and С in Paris’ equation predicting.

Our approach to this problem is presented below.

Analysis

The simplified shape of a Paris’ curve is presented on fig. 1.

К m/cycle

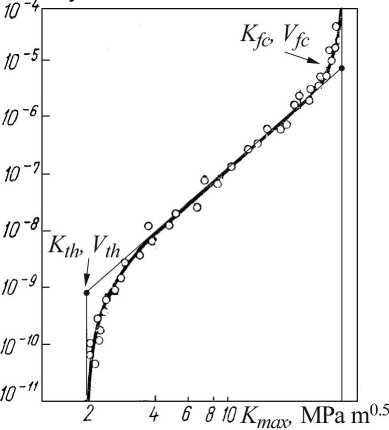
Fig. 1. The simplification of Paris’ curve

As can be seen from this figure, the reconstruction of a curve linear Region II may be done if the A K th , A K fc , and corresponding to them da/dN values are known. It makes possible to calculate constant n in Paris’ equation as:

n = ( lg v fc ^- lg v h ) ¹ ( lg ^A K c ^- lg ^A K th ) , ⁽²⁾ where v_th and v_fc – the crack propagation rates corresponding to A K th and A K fc .

Crack propagation rates in eqn. (2) are not known.

For this reason the assumption is accepted that the crack propagation rate is proportional to the small scale yielding zone width. In this case it makes possible to rewrite the eqn. (2) in the following form (3):

n = ( lg r fc ^- lg r h ) I ( lg ^A K fc ^- lg ^A K th ) ,      ⁽³⁾

where r_th and r_fc are the small scale yielding zones corresponding to A K th and A K fc . The r_fc and r_th values are determined as:

r fc

1L_M A K_

2п ( оy J, rth =

(1 — 2 Ц )² f A K h ) 2 п I S k ^J ,

where ц - Poisson’s ratio, S k - fracture stress.

In the eqn. (5), the substitution of an S_k value instead of о y is accounted for by the following reason. The A K_th determination procedure is carried out under conditions of a load decreasing. Thus, the crack propagation in this region is accomplished in the extremely hardened material.

It can be seen from eqns (3–5) that for the purposes of further analysis it is necessary to develop the non-direct methods for A K th and A K fc determination.

Discussion

We have proved the existence of a linear correlation between fracture toughness, К_Ic , and A K fc values for more than 40 different steels [5]. This relationship is shown on fig. 2 and is described by the following equation:

A K _fc = 0.8611 • K _Ic - 26.387.       (6)

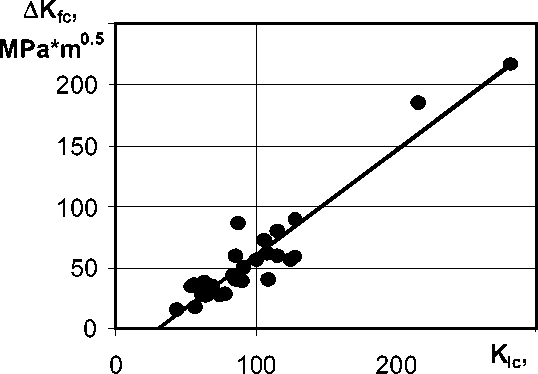
MPa*m0.5

Fig. 2. The relationship between К_Ic and Δ К_fc

Previously [1; 2; 8] the practical methods for fracture toughness К_Ic prediction through mechanical properties in tension and hardness values of materials were developed. The predicted К_Ic value may be used for Δ К_fc calculation through the eqn. (6).

The results of calculation Δ К_fc are presented in table 1.

In this work also the relationship between Δ К_th and σ _b/ σ _y was proposed (fig. 3).

It is valid for many different steels [4–6] and may be described by linear function:

Δ K_th = 36.906 ⋅ σ _b / σ _y - 34.04,     (7)

where σ _b is an ultimate tensile strength, σ _y is a yield stress.

The results of Δ К_th calculation are presented and compared to their experimental values in table 2.

It should be noted however that determining Δ К_th values is dependent on testing equipment.

Now, when the Δ К_th и Δ К_fc are already found, the n constant value in the eqn. (3) can be calculated. After that we have to find the С constant in eqn. (1).

The correlation between constants С and n in the Paris’ equation is known [3; 7]. We have confirmed this relationship for steels investigated in present paper. It can be described as:

C =0.0002⋅ e - 6.9048 ⋅ n (8)

The fair of this formula was shown for more than 200 different materials. The correlation coefficient value equals to 0.998. Thus in the linear region of a Paris’ curve the crack propagation rate is controlled by the single parameter С or n . The results are presented in tables 3, 4 and fig. 4.

As can be seen from the presented analysis the non-direct method for determination of all parameters of the Paris’ curve is developed. The calculated and experimental values of constants C and n are in good agreement.

Table 1

The comparison of results experimental and calculation Δ К_fc values

Steels	Т , К	σ 0.2 МPa	σ b МPa	Δ К fc МPa ∗ m (experiment)	Δ К fc МPa ∗ m (calculation)	δ , %
15KH2МFА	293	584	700	121.3	127.5	4.8
	243	647	752	59	63.8	7.5
	213	674	783	62	72.3	14.2
15KH2NМFА	293	593	707	129.4	132.8	2.6
	243	658	756	72.46	85.7	15.4
	183	745	943	34.2	42.9	20.2

The comparison of results experimental and calculation A K th values

Steels	Т , К	σ 0.2 МPa	σ b МPa	Δ K th МPa*m (experiment)	Δ K th МPa*m (calculation)	δ, %
15KH2МFА	293	584	700	9.1	10.19	-12
	243	647	752	12.4	8.85	28
	213	674	783	12.5	8.83	29
15KH2NМFА	293	593	707	9.2	9.96	-8.2
	243	658	756	10.2	8.36	18
	183	745	943	10.6	10.67	-19
St3sp	293	240	470	33.58	30.03	10.58
18Gsp	293	260	500	28.08	28.12	-0.13
09G2S	293	352	503	15.25	15.06	1.24

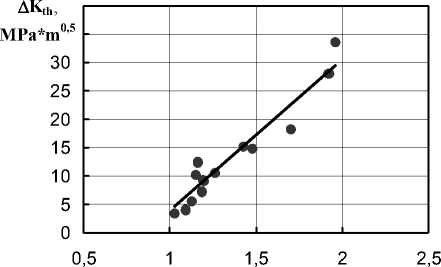
σ _b / σ _y

Fig. 3. The relationship between K K th and b b / a y

Table 2

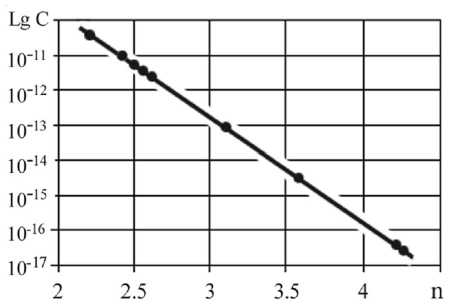
Fig. 4. The C dependence on a n value

For the lifetime prediction the Wilson’ approach can be used. The number of cycles, N, necessary for crack grows from the initial size а0 to the critical size acr can be found from the Paris’ equation as where Ab = bmax - a min, M - parameter of geometry and the shape of defect, we get

N = r---- d a

1 ₀ C ( A o^Ma ) n .

N = J

da

C ( A K ) ⁿ .

Integrating of the eqn. (11) results in

• ⁽⁹⁾    Wilson’ formula:

Assuming that                                            2	\ 1           1     1
A K = AbV Ma ,            (10)         N = ( n - 2) CMn 2 A ^ 1	( n - 2)/2      ( n - 2)/2 _ a о           aC r      _

Table 3

The comparison of results experimental and calculation n values

Steels	σ 0.2 МPа	σ b МPа	С (experiment)	С (calculation)	δ , %
20KH13 (1)	655	775	3.12	3.15	1.0
20KH13 (2)	566	749	2.89	3.04	5.1
14KH17N2	782	943	2.56	2.76	7.4
13KH11N2V2МF	885	1 015	2.86	2.88	0.9
08KH17N6Т	840	895	2.57	3.18	19.3
1KH16К4NМVFBА	980	1 163	2.56	3.51	27.1

Table 4

The comparison of results experimental and calculation C values

Steels	σ 0.2 МPа	σ b МPа	C (experiment)		C (calculation)		δ , %
20KH13 (1)	655	775	5.89	⋅ 10-9	6.07 ⋅	10 -9	2.9
20KH13 (2)	566	749	1.15	⋅ 10-9	1.27 ⋅	10-9	9.4
14KH17N2	782	943	6.71	⋅ 10-9	8.88 ⋅	10 -9	24.4
13KH11N2V2МF	885	1 015	3.82	⋅ 10-9	3.79 ⋅	10 -9	-0.8
08KH17N6Т	840	895	6.04	⋅ 10-9	4.72 ⋅	10-9	-27.9
1KH16К4NМVFBА	980	1 163	1.6 ⋅	10-8	1.99 ⋅	10-8	19.6

The a_cr value is found from the condition of the pressure vessel fracture or can be taken with consideration of crack size allowed for this structure.

The verification of the suggested model has shown its applicability for express lifetime estimation of different structures.

Conclusions

• 1.    The relationship between Δ K_th and σ _b/ σ _y ratio was found. The correlation Δ K_fc ( K_Ic ) was also demonstrated.

• 2.    The non-direct method for determination of Δ K_th and Δ K_fc and corresponding to them da/ dN values was developed.

• 3.    The method for prediction of Paris’ curve shape through the results of tensile test is suggested. It makes possible to estimate lifetime of different structures with cracks under cyclic loading.