The method of real options for evaluating the efficiency of gas project

Option to abandon

Option to expand

Option to contract

Compound option

Rainbow option

Valuation of investments in gas

Real options approach is used to analyze the investment decision in oil and gas production. The price of the option to invest is estimated using a binomial modeling and the backwards induction methodology. The assumption that prices evolve according to a binomial process and that investments in oil and gas are similar to investments in non-dividend paying assets permit us to state that an investor is indifferent to risk and requires no additional compensation for risk. In other words, the expected return on the investment is the risk free rate and the investment exists in a risk neutral world. The implication is that the option (to invest) can be valued on the basis that investor is risk neutral. Thus, the investor’s risk preference has no effect on the value of the option (to invest) when it is expressed as a function of the price of the underlying asset, i.e., oil and gas. As a result of the general principle of risk-neutral valuation used in option pricing, we can with complete impunity assume the world is risk neutral because the resulting option prices are correct in a risk neutral world as well as other worlds. This explains why the pricing formulas of Black-Scholes (B-S) for European calls, c and p for puts on non-dividend paying stocks do not involve the stock’s return, ^ ^.

c = S₀N ( d ) - Ye ^- rT N ( d^ )

p = Ye’ rT N ( - d ₂) - S₀N ( - d. )

where

d

+

r +

2 c

^

T

к к ² J )

d. =

+ r к

c Tt

= d

—

c Tt

It is well known that an analytical solution does not exist when valuing an American-type call option on a dividend-paying asset with positive exercise price

S

[See Hull, 2005]. Adapting the B-S model to this paper, the variables ⁰ is the price of the underlying asset , Y is the benchmark representing the reference price of the underlying asset that the investor must earn to justify future investments in oil and gas production; r is the risk free rate of return continuously compounded, T is the expiration date, &  is the volatility of the price of the underlying asset and the function N ^{( x} ) is the cumulative probability function for a standardized normal variable.

A generalized binomial model on risk neutral investments

S

Let ⁰ refer to the median price of the underlying asset and ^f is the option to invest in the underlying asset. The option to invest will expire in time, T . During the life of the option, the price of the underlying asset can move up from SS                                       f

⁰ to a higher level, ^u , and the payoff from the option is ^u . Conversely, the price

SS of the underlying asset can move down from 0 to a lower price d and the payoff from the option isfd. The inference is that u ^1.0; d ^1.0. In other words, the proportional increase in the price of the underlying asset when there is an up movement is u -1.0; and the proportional decrease in the price of the underlying asset when there is down movement is 1.0 - d•

Hypothetically, if the price of the underlying asset goes up, the value of the portfolio at the end of the option is

V = S_u A- f_u

If the price of the underlying asset goes down, the value of the portfolio becomes

V = S d a- f_d

The value of A that makes the portfolio riskless becomes Su A - fM = Sd A - fd f - f, ud

“ S_u — S d

Equation (1) shows that ^A is the ratio of the change in the price of the option to the change in price of the underlying asset as we move between tree nodes. We denote the risk free interest rate by r and the present value of the portfolio when the price of the underlying asset goes up becomes:

( s, a- f, e—rT

Conversely, the present value of the portfolio if the price of the underlying asset goes down is zero and the option is worthless:

( S d д- f d e - T = о

Now, suppose the cost of setting up the portfolio is s о д - f .

;

It then follows that

(Su д- fu e—rT=sо д- f,; and f = Sо д(1 - ue -rT)+ f„e-rT erT - d

P =-----

If we substitute equation (1) forд and u - d , the equation above becomes f =e

—

r ^T [ pfu ^{+( 1 -} P ) ^fd ]

^p is the probability of an up movement and ^{( 1 - p} ) is the probability of a down movement. Assuming that the price of the underlying asset will evolve along a binomial tree from N= 0 to N= 4 over four quarterly periods. Adapting SS

Barberis (2009), we can assign values to ^u and ^d based on the equations below.

S u = A T + \ ( a ² + CT ² ) T - ( a ² ) T

Sd = AT-f 2 + ct ² ) T - ( a ² ) ^T

We set ^A , and ^CT at ( ^A , ^{CT )} = ^{( 1.1} , ⁰ -3 ⁾ to represent the annual after tax median rate of return and standard deviation respectively. Thus the price of the underlying asset goes up u =1.1619, and down by ^{d = 0.8863.}

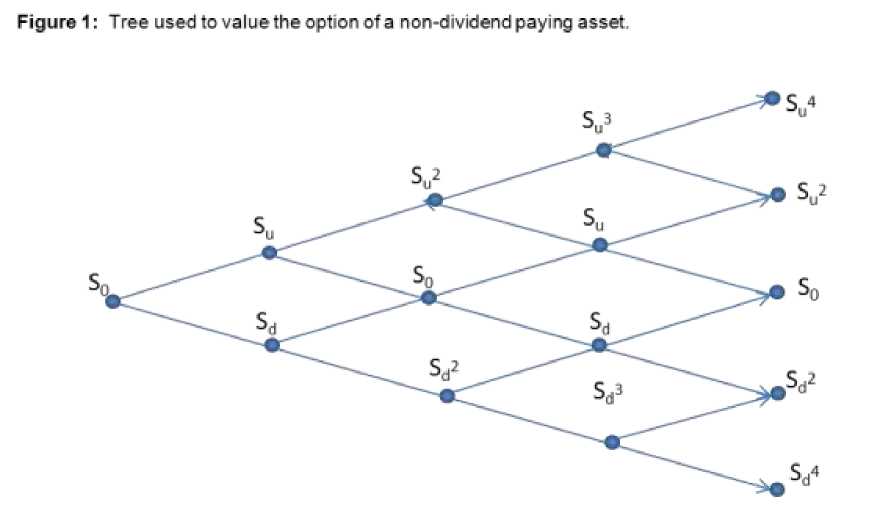
Figure 1 below illustrates the tree of prices when the binomial model is used. At time zero, the price of the underlying asset, S0, is known. At time дt there are two possible prices, Su and Sd; at time 2д t there are three possible prices, Su , Su and Sd and so on.

Accordingly equation (2) becomes f = e -r A T [pfM +(1 - p)fd]                        (3) and the expression for p becomes:

r A T e - d p =----- и ^{- d}                                   (4)

Repeated computations of equation (3) gives fu = e rAT \pfuu + (1 - p)fud ]                              (5)

^fd = ^e r ^A T [ pf ud ^{+ ( 1} - ^p ) ^fdd ^]                               (6)

Substituting equations (5) and (6) into (3), we get f = e

2 r ^a T [ p 2 f„ + 2 p ( 1 - p ) f ._a + ( 1 — p ) 2 Л , ]

Equation (7) is consistent with the principle of risk-neutral valuation discussed earlier. The variables, p 2 2p ( 1 - p ) and ( 1 - p ) 2 are probabilities that the upper, middle and lower nodes will be reached. The option price is equal to its expected payoff in a risk neutral world discounted at the risk free rate. As we add more steps to the binomial tree, the risk neutral valuation principle continues to hold.

The use of Real Option analysis can add more value to oil field developments compared to traditional methods of making investment decisions. Since real options adds flexibility to projects, it can save upfront capital expenditure for instance in the amount of money spent on initial facility size/capacity since alternatively some limited capacity could have been added with the flexibility to add more at a later time.