The New Block Cipher Design (Tigris Cipher)
Автор: Omar A. Dawood, Abdul Monem S. Rahma, Abdul Mohsen J. Abdul Hossen
Журнал: International Journal of Computer Network and Information Security(IJCNIS) @ijcnis
Статья в выпуске: 12 vol.7, 2015 года.
Бесплатный доступ
In the present paper we have proposed a new variant of AES cipher with high level of security and an elegant construction called TIGRIS cipher. The TIGRIS name has been derived from one of the two famous rivers in Iraq. The proposed TIGRIS cipher is a revision for the proposed Euphrates cipher which has already been published. It has been designed with a good coherent structure that is based on solid algebraic and well mathematical opinions. The proposed cipher uses the SPN structure and what is known by the Galois Field GF (28). It is an iterated cipher that has a conservative design which is easily implemented on both hardware and software. It operates with block size of 128-bits and with three variable key lengths of 128-bits, 192-bits and 256-bits in addition to sixteen rounds or multiples of four rounds. The proposed cipher works with good invertible operations' stages and a compact duplicated ciphering key. The Tigris cipher construction strategy includes the adoption of construction a new S-box with high non-linearity that uses the same routines of the AES-S-box stage but with different modular arithmetic of irreducible polynomial and different affine matrix in addition to the distinct constant vector. The second and the third layers of the proposed model are based on the shifting concept for the confusion and diffusion process with reversible operations. The last layer of the proposed model is the key addition layer that is responsible for the expanding and generating the ciphering key by two directions those of row and column expansion, which are associated with two constant vectors of golden ratio and base nature algorithm as a fixed word to eliminate any weak or semi-weak ciphering key.
Block Cipher, Symmetric Cipher, Advance Encryption Standard (AES), Data Encryption Standard (DES), Substitution and Permutation Network (SPN), Feistel Structure (FS)
Короткий адрес: https://sciup.org/15011478
IDR: 15011478
Текст научной статьи The New Block Cipher Design (Tigris Cipher)
Published Online November 2015 in MECS
The last decade witnessed proposing of several symmetric ciphers that are so far related to our proposed model.
In Joan Daemen and Vincent Rijmen in [5] proposed a marvelous standard symmetric cipher which has been candidate as the official cipher for the commercial software and hardware in 1999, then was selected in 2001 to be the winner among several candidates ciphers in order to be the Advance Encryption Standard (AES).
In 2015 Omar Dawood, Abdul Monem Rahma and Abdul Mohsen Abdul Hossen have proposed a new symmetric cipher called “The Euphrates Cipher’ which is considered the sister of Tigris cipher that paved the way to the design of Tigris cipher and participated mainly in inspiring most of its construction ideas. The Tigris cipher inherited most of its properties and the good features from the Euphrates cipher [6].
Gil-Ho Kim, Jong-Nam Kim and Gyeong-Yeon Cho proposed a new model of the symmetric cipher with symmetry of SPN structure that can be implemented efficiently with one structure. The proposed structure can be applied to those algorithms that encrypt and decrypt the data with different structures to encrypt with the same structure but for even rounds that lead to reduce hardware and lessen the consuming time [7].
ALI ABDULGADER et al in [8], submit a new method of the AES cipher by depending upon the chaotic map and the shifting register technique for the image encryption. The proposed cipher presents S-box construction with circular shifting based on the specific of constant round equation. The main purpose for this method is to increase the image encryption with a reduced time.
Md. Nazrul Islam in [9] suggests a new revision of an extended AES cipher that encrypts and decrypts data with block size of 200-bit instead of 128-bit and enlarged the ciphering key to 5x5 state matrixes. The proposed cipher applies a high margin of security but with less efficiency than the original of AES cipher.
-
III. Advanced Encryption Standard (AES)
NIST invited researchers and specialist designers in addition to the academic researchers in cryptographic field to submit their algorithms to be selected as AES. Five finalist candidates algorithms were chosen as the AES standard after a deep analysis and evaluation in August, 1999: 1) MARS (IBM)-complex, fast, high margin security [10], 2) RC6 (USA) – very simple, very fast, low margin security [11], 3) Rijndael (Belgium) -clean, fast, good margin security [12], 4) Serpent (Euro) -slow, clean, very high margin security [13], and 5) Twofish (USA) - complex, very fast, high margin security as the result Rijndael cipher was the winner cipher [14]. In October 2001, the algorithm Rijndael which is developed by the two Belgian scientists selected to become the Advanced Encryption Standard (AES). This was to replace DES cipher due to advances in cryptanalysis and the power processing that was no longer considered to be secure in addition to the vulnerable to the brute force attack [15]. AES is a symmetric key cipher that processes128-bit blocks and support key-lengths of 128-bits, 192-bits and 256-bits bits with 10, 12 and 14 round respectively. It consists of four main operations: SubByte, ShiftRow, MixColumn and Round Key Addition, that can be explained below briefly [16].
-
A. SubByte Transformation
This is the first stage in the round of AES cipher that is responsible for the confusion property. It is intended to achieve a non-linear substitution cipher as was discussed in [17]. The non-linearity is an important property for a block cipher to prevent differential cryptanalysis.
-
B. ShiftRow Transformations
This stage operates on each row of the state; it is intended to achieve a mixture of bytes positioned in different places of a plaintext message block. This layer increases the diffusion property by distributing the bytes positions to other positions without changing the elements values.
-
C. MixColumn Transformations
This stage operates on each column of the state; it is a mixture of bytes in different positions of a message block that causes a wider distribution of messages in the whole message space using the linear equation in forward and the inverse in the backward process with matrix representation. The final round does not include the mixcolumns operations
-
D. The Round Key Addition
The Round Key Addition provides a necessary secret randomness to the message distribution. This transformation consists of XORing the Round Key to the state matrix and it is denoted by: AddRoundKey(State, RoundKey). The Round key addition is corresponding to the whitening concept that comprises the pre-addition of the ciphering key to the first and the last round [18].
-
E. Key Schedule
The round keys are derived from the cipher Key by means of the key schedule. This means consisting of two components: the Key Expansion and the Round Key Selection that is responsible for the generating of all the ciphering subkeys in each round from the algorithm [19].
-
IV. The Algebraic Polynomial Preliminaries
The algebraic polynomial represents the backbone in the AES construction and especially in the work of the inner operations over the algebraic structure, Let A an algebraic polynomial with addition and multiplication over A with the expression of the form:
n
F(x) = £ aiX i=0 (1)
Where n is a non-negative integer elements, the coefficient a , 0 ≤ i ≤ n are element in A , and x is a symbol not belonging to A , the coefficient a n is called the leading coefficient and is not the zero element in A for n ≠ 0 [20].
The integer n with the following formula is called the degree of f(z) and is denoted by n = deg(f(x))=deg(f). If the leading coefficient is a0, then f is called constant polynomial. If the leading coefficient is a0=0; then f is called the zero-polynomial and is denoted by f=0. So the A[x] will represent the set of all polynomials over algebraic structure A [21] .
For f, g e A[x] with
F(x) = Ya,^ «d g(x) = УДх'(2)
-
i=0
We have max(n,m)
F(x) + g(x) = i=0
where
(at + bi i = 0,1,..., min (n, m) ai i — m+ 1, ...,n bi i = n + 1... ,m)
n + mn
F(x), g(x) = Y CfcXk where ck= Y ai bj k =0 i+j = k
0 < i < n
0 < j < m
It is easy to see that if A is a ring, then A[x] is a ring with A being a subring of A[x]. Addition and multiplication between polynomial over a ring will result in the following relationship on the polynomial degrees [22].
deg (f + g) ≤ max( deg ( f ),deg ( g )), deg ( f g ) ≤ deg ( f ) + deg ( g )
Now if A is a field, then because a field has no zerodivision we will have cn+m = anbm ≠ 0 for an ≠ 0 and bm ≠ 0.
So if A is a field, then deg ( fg ) = deg( f ) + deg( g ) (4)
Let f, g e A[ x ] such that g ^ 0 . Analogous to the case of division operation between integer numbers. We can always rewrite the ( f ) with the formula below :
f = gq + r for q, r e A[x] with deg (r) < deg (g) [23] .
For the Galois field with order (p) of GF(p), where p is a prime number, that has a ring properties which can be addressed as a set of finite elements modulo p. So the set of integers in GF(pn) can be represented as polynomials of degree n-1 in GF(p). All operations are implemented modulo m(x) where m(x) is modular reduction of an irreducible polynomial that has the same properties of prime number in integer calculations [24].
The reducible polynomial comprehension means the polynomial that can be factored into a product of polynomials of smaller degree to its factors; the polynomial is called irreducible if it has no divisors other than 1 and itself. The other important mathematical term is the primitive polynomial that involves a polynomial number that generates all elements of an extension field . So the primitive element is an element in the field with the property that raising it to an ever increasing (integer) refers to the power that generates all the nonzero elements within a field. It is also sometimes called a generator element [25].
-
V. The Proposed Cipher
The TIGRIS cipher uses 128-bit message block length (i.e. 16 bytes) and 128-bit, 192-bit and 256-bit key lengths the same lengths that supported by AES except with different number of rounds. The message block and the ciphering key can be realized as a 4*4 state matrix. Each state matrix represents as 16 positions (4*4) bytes which are equal to 128-bits. The proposed cipher uses basically 4 main functions. These are Xored add operation between the message block and the round key (AddRoundKey), S-box tables (SubByte operation), row shifting (RevisibleShiftRows) and mixing each column in the matrix (ShiftingMixcolumn). It performs efficiently in applications with low covered area resources and the applications that need high-speed cryptosystems to speed up high-bandwidth data transfers and to protect privacy. TIGRIS cipher designed to apply high volume of protection and high resistant to malicious attacks. It provides an efficient and elegant key schedule (key setup) that expands in two directions in rows/columns states which lead to increase the complexity of key generation and eliminate the weak and semi-weak keys in generation process with duplicate cipher key generation.
-
VI. Rational Design
The rational design for this model is to design an elegant algorithm with coherent structure and high margin of security. The proposed cipher is designed to satisfy the modern era requirements and the future needs.
So, the proposed cipher is focused on the performance and the speed of the algorithm in addition to the security aspects with simplicity in design idea, which leads to figure out the algorithm and explains the entire aspects of design rationale, implementation and description of encryption and decryption process. This cipher provides a good resistance against theoretical and practical cryptanalytic attacks, since it uses a complex operation and extra bit wise operations with two constant vectors as a constant word in its key generation process as well as many attacks that have been taken into account. The proposed algorithm is usually designed so as to be implemented in both software and hardware efficiently. However, there is no set of rules one can follow to achieve this goal. We have designed TIGRIS algorithm taking into account many elements such as gate counts, memory requirements in smart card implementations, and software performance on multiple platforms.
-
VII. Design Criteria
There are many public criteria in designing any algorithm, but the most important principles which can rule and determine the nature, design and characteristics of the cipher system is the mathematical bases that they use, so this cipher is designed according to several criteria:
-
1- High margin of security
-
2- Design simplicity with repetitive shifting
-
3- Conservativeness
4-Cost reduction in hardware
box) which is used in TIGRIS cipher is so far similar to the one that is used in the AES cipher on one hand of the design method and the mathematical representation on the other. The S-box stage is the basic nonlinearity stage in the cipher that works with byte operations. The proposed S-Box constitutes from two levels. The first level of designing process takes byte by byte as single value in the GF (28) and applied the multiplicative inverse on each one separately. The multiplicative inverse computed modulo the following irreducible polynomial of x8 + x5 + x3 + x2 + 1. The second level represents the resultant hexa-value which is treated as a vector through the calculating of linear affine over GF(2) as stated in equation(5), and the resultant number Xored with the constant vector represented by the value (59) as stated below affine matrix. The final outcome is the forward S-box which is stated in Table 1.
b ' 1
b ' 2 b ' 3 b ' 4 b ' 5
b '
b ' 7
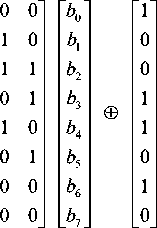
-
VIII. TIGRIS Structure
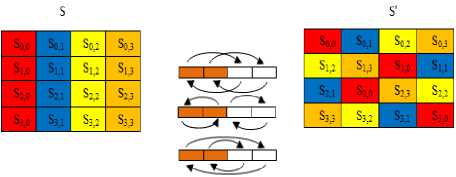
The structure of TIGRIS cipher is one of the most prominent changes that discriminate TIGRIS cipher from the AES and its predecessor’s ciphers, see Fig. 1, at the end of this paper, in spite of several algorithms built by depending upon the AES ideas and their structural characteristics. So, the round transformation of the proposed cipher also consists of the same four stages operations. The TIGRIS cipher has a flexible structure with high non-linearity in SubByte operation and the similarity in Shifting Rows that need no inverse. In addition to the extra shifting operations in diffusion layer (ShiftingMixcolumn) that repetitively recur for each four rounds with shifting the equation of mixcolumn four times to generate four different equations with the same coefficients. But in a different arrangement that needs a different inverse. The number of equations will be equal to the order degree of the linear equation of mixcolumn. The round key generator uses a compact method that generates the round key addition by two directions in column state and in row state with two (F) functions, as a result the two generated ciphering keys Xored together with two constant vectors represented by golden ratio and base natural algorithm to produce the generated ciphering sub-key in each round.
-
A. Tigris-Subbytes Transformations
One of the most critical and expensive operations in any cipher design is the substitution, the substitution (S-
Table 1. Tigris-Forward S-Box
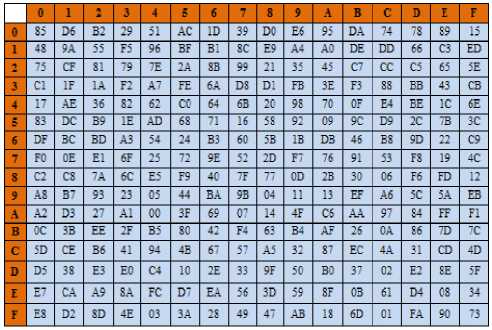
-
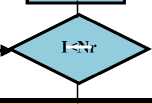
B. Tigris-InvSubyte Transformations
The inverse of the proposed S-box is constructed by applying the inverse of the affine transformation followed by applying the Xored with the constant vector that is represented by the value ( BD ) as shown in equation (6), and the resultant takes the multiplicative inverse in GF(28) module the mentioned irreducible polynomial. The consequence is stated in Table .2 below. The core idea for using constant vector is to increase the complexity of the S-box and to remove fixed point respectively.
Add round key (State, Round)
I= 1
SubByte (State )
ReversibleShiftRows (State )
ShiftingMixcolumn(State)
Add round key (State, Round)
SubByte (State)
ReversibleShiftRows (State )
ShiftingMixcolumn(State)
Add round key (State, Round)
|
SubByte (State) |
||
|
ReversibleShiftRows (State ) |
||
|
ShiftingMixcolumn(State) |
||
|
Add round key (State, Round) |
||
SubByte (State)
key Schedule
ReversibleShiftRows (State )
ShiftingMixcolumn(State)
Add round key (State, Round)
I=I+1
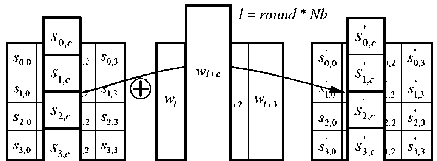
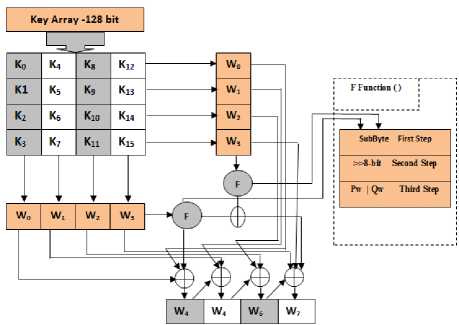
I SubByte (State ) ReversibleShiftRows (State ) Add round key (State, Round) Fig. 1. General Structure of the Tigris Cipher bo 0 1 b'1 00 b 2 1 0 b 3 _ 1 1 b 4 = 1 1 b 5 1 1 b 6 0 1 b' 7 . .1 0 1 0 b0 11 b 11 b 2 11 b 3 01 b 4 10 Ь5 01 b6 0 0. . b 7 1 0 1 1 (6) ® . 1 1 0 [1. Table 2. Tigris-Backward S-Box C. Tigris-RevisibleShiftRows The purpose of the step RevisibleShiftRows is to spread the bytes of each input column to different output columns. This step is a linear diffusion process that operates on individual rows and each row of the array is rotated by a certain number of byte positions. The first row (row 0) is not shifted, and the remaining rows proceed as follows 2nd, 3rd and 4th rows 2-bytecircular left shift is performed, see Fig. 2, For decryption process, the same corresponding steps shifts the rows in exactly, implemented with the same direction. This is a good method to obtain an optimal diffusion with low cost on hardware and high fast implementation in addition to gain resistance against truncated differential attacks and saturation attacks. The RevisibleShiftRows process introduces an optimal diffusion with acceptable linearity. Fig. 2. RevisibleShiftRows D. Tigris-ShiftingMixcolumn Similarly to the AES round function, the ShiftingMixcolumn transformation in TIGRIS takes a 4×4 matrix of bytes, which passes each byte to the shifting and multiplying in order to apply some linear transformation to the result. This linear transformation is called the "ShiftingMixcolumn". The ShiftingMixcolumn provides better diffusion and better protection against differential attacks. The ShiftingMixcolumn in this model uses the same equation of the original cipher except it makes a shifting to the one vector of the matrix. The forward ShiftingMixcolumn depends on the row shifting, for each last row of matrix becomes the first row in the next new matrix and so on. So, for each four rounds it will repeat these operations. This step involves shifting left and exclusive-ORing bits with themselves. These operations provide both confusion and diffusion properties. The forward and backward equations can be stated in equation (7) and equation (8) with the shifting for the matrix of mixcolumns operations as follows: a(x)= {03}x3 + {04}x2 + {01}x + {07} (7) b(x)= {0b}x3 + {08}x2 + {09}x + {0b} (8) a(x) * b(x) = I Where I identity matrix "07 01 04 .03 03 04 07 03 01 07 04 01 01 04 03 07. 0 "0 b 09 08 .0 b 0b 08 0b 0b 09 0b 08 09 09" 08 0b 0b. = "01 00 00 01 00 00 .00 00 00 00 01 00 00 00 00 01 " . " S0 c "07 03 04 01" S 0,c " "0 b 0b 08 09" S'0,c " S’, 01 07 03 04 Sic 09 0b 0b 08 S 1 0 = 1 c 0 = 1 c S'2 c 04 01 07 03 S2,c 08 09 0b 0 b S 2 c . S3 c .03 04 01 07 S 3c. .0 b 08 09 0b. .S 3 c. Г S' 0 c "03 04 01 07" S 0,c ’ "09 0b 0b 08" S\c " S’, 07 03 04 01 S 08 09 0b 0b S 1c 0 = 1 c 0 = 1 c S’ c 01 07 03 04 S2 c 0b 08 09 0b S 2 c . S’ c .04 01 07 03. .S3 c. .0 b 0b 08 09. .S 3 c. ■ S0c "04 01 07 03" " S 0,c "08 09 0b 0 b" ■ S\c" S', 03 04 01 07 S1c 0 b 08 09 0b S 1 c 0 = 0 = 1 c S2c 07 03 04 01 S 2,c 0 b 0b 08 09 S 2 c . S\c .01 07 03 04. .S 3c .09 0b 0b 08. .S 3 c. " S0c "01 07 03 04" "S0 c" "0 b 08 09 0b" "S 0 c" S', 04 01 07 03 Sc 0 b 0b 08 09 S\.C c 0 = 1, C 0 = S\c 03 04 01 07 S2c 09 0b 0b 08 S^c .S’ 3c .07 03 04 01. . S3c .08 09 0b 0b. S3c E. Tigris-Inverse ShiftingMixcolumn The backward ShiftingMixcolumn (Inverse ShiftingMixcolumn) relies on shifting column, for each last column of matrix becomes the first column in the next new matrix and so on for each four rounds also will repeat these operations, in order to superpose the same sequence of forward matrices representative by shift rows. F. Tigris-Round Key Addition In this operation the Round Key is applied to the state matrix by a simple bitwise XOR operation. The round key addition is derived from the cipher key by means of the key schedule. The transformation that consists of EXORing Round Key to the State array which denoted by AddRoundKey (State, RoundKey) as shown in Fig. 3 below. Since, there is no prominent distinct or remarkable difference between the addition and subtraction operations in the finite field, because the two operations are considered the same. Fig. 3. Round Key Addition G. Tigris-Key Schedule Key schedule is the main part of the key expansion that is responsible for accepting a 128-bit input key and producing 128-bit ciphering key which represents the secret key. The key expansion specifies how expanded key is derived from the cipher key, because the encryption and decryption processes require one round of ciphering key for the initial key block, which is treated nearly as a seed for generating a new ciphering key for each round. The key expansion has been modified to be possible to execute the key schedule using a small amount of working memory with high key agility on a wide range of processors that is implemented with two constants vectors to eliminate any symmetries or weak keys, represented by base natural algorithm and golden ratio in order to give an efficient diffusion of cipher key differences into the expanded key. The ciphering key is generated by rows and columns directions as stated in Fig. 4. Note Pw = base natural algorithm (b7e15163), Qw = golden ratio (9e377969) << 8-bit =right rotate over the vector Fig. 4. TIGRIS Key Expansion There are several advantages and limitations that really determine the nature’s work of this algorithm and explain its characteristics that can be stated as follows: A. Advantages Our proposed cipher has several useful characteristics that can be listed as follows: • Our proposed algorithm can be implemented to run fast. So there is a compact trade-off between the strong/performances in implementation and flexibility. • It gives more resistance against all the attacks because it is based on increasing the confusion and diffusion layers. • Our proposed algorithm can be implemented on a smart card and with a small amount of memory. • The proposed cipher adopted the reversible technique in most stages of the round transformation in order to make the cost reduction in hardware devices. • The key generator for the key scheduling is duplicated for each round that works with two directions by rows and columns. So the complexity is increased rapidly with number of rounds. B. Limitations The limitations of the cipher have to do with its inverse: • In hardware, larger code and gate count and slower execution time comparative with the AES, but in general it submits a reasonable implementation time. • A reduced key agility and requires a longer time for the key setup than the original AES, but from the security view point, it is more secure. • In software, It uses two different structures one for encryption and the other for decryption. So this cipher will require more effort in programming code and in embedding devices with restricted hardware. • This algorithm is more secure but less efficient than the AES algorithm from some aspects. Our design philosophy was based on offering a high level of security. To do so, we designed the proposed cipher with very large security aspects. It has been designed on the basis of the theory of provable security against differential and linear cryptanalysis. The proposed cipher submit a full diffusion property to prevents the mounting of shortcut attack, since it depends on reversible shiftrows to get an optimal diffusion and also depends mainly on an iterated ShiftMixColumn transformation for each four rounds that reduces the space through which the plaintext can be exploited and increased the linearity. The developed RevesibleShiftRows stage considers another layer of linearity that means the absence of implementation attacks which exploit its internal structure. TIGRIS algorithm proposed with new design of strong and efficient key-schedule algorithm to defeat different types of attacks. The compact key expansion method increases the probability of keys that leads to increase the difficulty in brute force attack and dictionary attack. TIGRIS structure also increased the difficulty of differential power analysis (DPA) attack by the needs to the extra time of computations to the mathematical operations and to the internal state of the process in, since it has an innovation key setup and an effective mechanism to overcome possible threats. Solid algebraic methods that have been depended were to thwart any algebraic attacks. The proposed cipher can perform the encryption/decryption process in parallel and balancing way. Table 3 states the executive time in comparison for the proposed cipher and the AES algorithm. Table 3. Comparison of Execution Time between TIGRIS Cipher and the AES Algorithm Algorithms Block Size Key Size Time of Encryption in Ms. Original-AES (Rijndael) 128-bit 128-bit 0.0468 192-bit 0.0476 256-bit 0.0498 TIGRIS Cipher 128-bit 128-bit 0.0493 192-bit 0.0516 256-bit 0.0530 This paper describes a new secret-key block cipher that is called Tigris cipher which is aimed at a securing fast encryption of data. Tigris cipher produces an adequate security and submits deeper insights in developing other ciphers. The main structure is adamantine and the internal operations work cohesively. Since, it is based on pure algebraic and cryptography basis. TIGRIS cipher is a compact and high-linearity cipher suitable for a limited resource environment such as sensors, mobile devices and networks. Encryption and decryption operations in the proposed cipher are possible to be executed with low costs and overhead in addition to the low power consumption. This cipher addresses several issues related to adopt a new stronger key-scheduling algorithm that is convenient for the sensitive and real time applications. Acknowledgment The authors would like to extend special thanks to Dr. Hazim H. Muarich for his great contribution in editing and proof reading this paper from a linguistic point of view.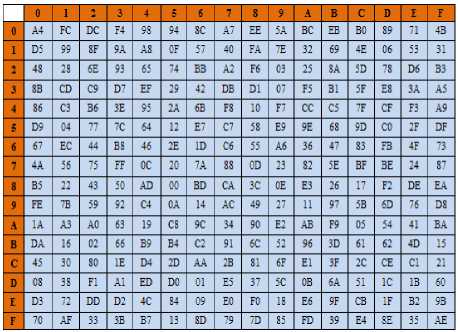
IX. Advantages and Limitations
X. Security Analysis
XI. Conclusions
Список литературы The New Block Cipher Design (Tigris Cipher)
- Kevin Sean Chan," A Block Cipher Cryptosystem UsingWavelet Transforms Over Finite Fields", IEEE TRANSACTIONS ON SIGNAL PROCESSING, VOL. 52, NO. 10, OCTOBER 2004, pp2975-2991.
- M. Girault, L. Juniot and M.J.B. Robshaw, "The Feasibility of On-the-Tag Public Key Cryptography", France Telecom Research and Development, 2005.
- P. Kitsos, Sklavos, M.D. Galanis and O. Koufopavlou, P. Kitsos et al, "64-bit Block ciphers: hardware implementations and comparison analysis", Computers and Electrical Engineering 30 (2004), pp593–604.
- "Announcing the ADVANCED ENCRYPTION STANDARD (AES)", FIPS 197, Ed: NIST, 2001.
- Daemen, J.; and Rijmen, V. (2002). The design of AES- The advance encryption standard. Springer-Verlag.
- Omar A. Dawood, Abdul Monem S. Rahma and Abdul Mohsen J. Abdul Hossen, "The Euphrates Cipher", IJCSI International Journal of Computer Science Issues, Volume 12, Issue 2, March 2015. pp154-160.
- Gil-Ho Kim, Jong-Nam Kim and Gyeong-Yeon Cho, "Symmetry structured SPN block cipher Algorithm", IEEE Xplore, Feb. 15-18, 2009 ICACT 2009 pp1777-1780.
- ALI ABDULGADER et al, "ENHANCEMENT OF AES ALGORITHM BASED ON CHAOTIC MAPS AND SHIFT OPERATION FOR IMAGE ENCRYPTION", Journal of Theoretical and Applied Information Technology 10th January 2015. Vol.71 No.1© 2005 - 2015 JATIT & LLS.
- Md. Nazrul Islam, "Effect of Security Increment to Symmetric Data Encryption through AES Methodology", Ninth ACIS International Conference on Software Engineering, Artificial Intelligence, Networking, and Parallel/Distributed Computing, 978-0-7695-3263-9/08 $25.00© 2008 IEEE.
- IBM MARS Team, "MARS and the AES Selection Criteria", May 15, 2000.
- Ronald L. Rivest1, M.J.B. Robshaw and Yiqun Lisa Yin, "The Security of the RC6TM Block Cipher", RSA Laboratories Version 1.0, August 20, 1998.
- Sam Trenholme, "A description of AES, the Advanced Encryption Standard", Writings and Projects, Lecture Notes, 2005. Available at this web: http://www.samiam.org/links.html.
- R. Anderson, E. Biham, and L. Knudsen, \Serpent: A Proposal for the Advanced Encryption Standard," NIST AES Proposal, 1998.
- B. Schneier et al, "TwoFish: A 128-bit block cipher", 15 June, 1998.
- Saddaf Rubab and Dr. Younus Javed, " Efficient Image Steganogrphic Algorithms Utilizing Transforms: Wavelet and Contourlet with Blowfish Encryption", I. J. Computer Network and Information Security, 2015, 2, 15-24.
- Omer K. Jasim Mohammad et al. "Innovative Method for Enhancing Key Generation and Management in the AES Algorithm. I. J. Computer Network and Information Security, 2015, 4, 14-20, Copyright MECS.
- Lingguo Cui, "A NEW S-BOX STRUCTURE NAMED AFFINE- POWERAFFINE", International Journal of Innovative Computing, Information and Control, Volume 3, Number 3, June 2007.
- Ali M. Saggheer, Salah S. Al-Rawi and Omar A. Dawood", Proposing of Developed Advance Encryption Standard. The fourth International Conference on Developments in eSystems Engineering DeSE 2011, IEEE Computer Society, pp 197-202.
- Yang Xiao et al, "Performance Analysis of Advanced Encryption Standard (AES)", 1-4244-0357-X/06/ 2006 IEEE.
- Carlos Cid, "Some Algebraic Aspects of the Advanced Encryption Standard", H. Dobbertin, V. Rijmen, A. Sowa (Eds.): AES 2004, LNCS 3373, pp. 58–66, 2005.©Springer-Verlag Berlin Heidelberg 2005.
- Carlos Cid, Sean Murphy and Matthew Robshaw, "Algebraic Aspects of the Advanced Encryption Standard (AES)", Springer, 2006.
- M. Ram Murty, "Problems in Algebraic Number Theory", Graduate Texts in Mathematics 190, Second Edition, Springer, March 2004.
- Wenbo Ma, "Modern Cryptography Theory and Practice", Copy right © by Hewlett-Packard Company, 2006.
- John M. Howie, "Fields and Galois Theory", undergraduate mathematics series, © Copy right Springer-Verlag London Limited 2006.
- Gabriele Nebe Eric M. Rains and Neil J. A. Sloane, "Self-Dual Codes and Invariant Theory", Algorithms and Computation in Mathematics Volume 17, Copy right ©Springer-Verlag Berlin Heidelberg, 2006.


